1.基础知识

1.1 K-Means 算法

• 定义：K-Means 是一种无监督学习算法，用于将数据集分成 K 个簇，簇内点尽可能相似，簇间点尽可能不同。通过反复计算簇中心和分配点到最近的簇中心来达到聚类效果。
• 用途：
  • 客户细分：将客户按消费行为分组，如根据消费习惯、消费金额等分成高价值和低价值客户群体。
  • 图像压缩：通过聚类减少像素颜色的种类，压缩图像。
  • 文档分类：基于文档特征（如词频）将文档分成不同主题类别。
• 适用场景：
  • 数据集较大时能快速聚类。
  • 数据的簇形状接近球形，适合分布规则的数据集。
  • 不适合簇形状不规则的复杂数据集。

1.2 层次聚类（Hierarchical Clustering）

• 定义：层次聚类基于构建层次结构分组数据，分为凝聚式（自下而上）和分裂式（自上而下）。凝聚式将每个点视为一个簇，逐步将最近的簇合并，分裂式则从一个大簇开始，不断细分。
• 用途：
  • 基因表达分析：分析基因的表达模式，构建基因树或分类模型。
  • 市场细分：通过层次化分割市场，找到小而精确的目标客户群体。
  • 图像分类：构建图像分类树，分析不同类别的层次关系。
• 适用场景：
  • 适用于小规模数据集或希望得到层次结构的聚类结果。
  • 当需要对数据进行层次结构的可视化展示时（例如树状图）。
  • 计算量较大，通常不适用于非常大的数据集。

1.3 密度聚类（DBSCAN）

• 定义：DBSCAN 基于密度来聚类数据，识别密度高的区域为簇，稀疏区域为噪声点。它可以发现任意形状的簇，无需指定簇的数量。
• 用途：
  • 地理空间数据分析：可用于分析具有空间坐标的数据，如建筑物分布、人口密度等。
  • 异常检测：识别噪声和异常点，如信用卡欺诈检测和网络入侵检测。
  • 社交网络分析：发现社交网络中群体性高密度区域，分析社交群体的结构。
• 适用场景：
  • 适用于含有噪声和形状不规则的簇，例如地理、空间数据库。
  • 当簇的形状较复杂，且希望自动处理噪声点时效果较好。
  • 对密度差异较大的簇不适用，并且对参数选择（邻域半径 ϵ\epsilonϵ 和最小样本数 MinPts）较敏感。

1.4 距离和相似度度量方法

• 定义：在聚类算法中，距离和相似度是衡量数据点之间关系的重要指标。选择合适的距离或相似度度量方法可以影响聚类结果的质量。
• 用途：
  • 欧式距离：常用于几何上连续数值特征的距离计算，适合 K-Means 和层次聚类等需要计算几何距离的场景。
  • 曼哈顿距离：适合分隔在网格结构上的点（例如城市街道间的距离计算）。
  • 马氏距离：适合高维数据，能够考虑特征之间的相关性。
  • 汉明距离：常用于字符串或序列数据间的差异比较（如基因序列分析）。
• 相似度度量：
  • 余弦相似度：用于度量两个向量的方向相似性，常用于文本数据或高维数据。
  • 皮尔逊相关系数：用于度量两个变量之间的线性关系，常用于统计分析。

适用场景：

• 欧式距离：适用于几何形状规则的数据，尤其是平面或多维空间中的数据。
• 曼哈顿距离：适用于数据分布呈网格状或有明确方向的情况。
• 马氏距离：适用于高维数据集，数据具有相关性时表现优越。
• 汉明距离：适用于二进制向量、字符串或基因序列比对，主要应用于计算离散数据的相似度。

1.5 总结：

• K-Means：适合规则分布的大规模数据，快速聚类。
• 层次聚类：适合小规模数据和需要层次结构的场景，如基因分析或市场细分。
• DBSCAN：适合处理复杂形状簇和含有噪声的数据，如地理空间数据或异常检测。
• 距离和相似度度量：用于选择合适的距离度量方式，根据数据的特征进行优化选择。

这些算法在不同的应用场景中表现各异，建议根据数据特点选择合适的算法。如果有其他问题或需要深入探讨，可以随时提问！

---

2.K-means 算法对鸢尾花（Iris）数据进行聚类

2.1 导入所需的模块

2.1.1 代码片段：

import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.cluster import KMeans
from sklearn.preprocessing import StandardScaler

2.1.2 实现目的：

导入必要的库，用于数据加载、标准化处理、执行聚类算法以及绘图。

2.1.3 代码解释：

1. import matplotlib.pyplot as plt：导入 matplotlib 库中的 pyplot 模块，并将其命名为 plt，用于后续的可视化操作。pyplot 是 matplotlib 中的一个子模块，它提供了一组类似 MATLAB 风格的命令，用于创建图形、控制图形元素等。
2. from sklearn.datasets import load_iris：从 sklearn.datasets 中导入 load_iris 函数，用于加载经典的鸢尾花数据集。load_iris() 会返回一个类似字典的对象，包含特征数据、目标标签以及数据描述。
3. from sklearn.cluster import KMeans：从 sklearn.cluster 模块中导入 KMeans 类，K-Means 是一种常用的无监督聚类算法，用于将数据集分成预定义数量的簇。K-Means 会将数据分配到不同的簇，使得簇内数据相似度最大，簇间数据相似度最小。
4. from sklearn.preprocessing import StandardScaler：从 sklearn.preprocessing 模块中导入 StandardScaler 类，用于对特征数据进行标准化。标准化的作用是使每个特征的数据均值为 0，标准差为 1，从而消除特征之间由于不同尺度带来的影响。

2.2 加载并标准化鸢尾花数据集

2.2.1 代码片段：

iris = load_iris()
X = iris.data  # 特征数据
y = iris.target  # 实际标签（用于后续比较）
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

2.2.2 实现目的：

加载鸢尾花数据集，并对数据进行标准化处理，使特征在同一尺度下便于进行聚类分析。

2.2.3 代码解释：

1. iris = load_iris()：通过 load_iris() 函数加载鸢尾花数据集，并将其保存到变量 iris 中。该数据集是一个包含 150 条样本的数据集，每个样本有 4 个特征，并且分为 3 个类别（Setosa, Versicolor, Virginica）。
2. X = iris.data：从 iris 数据集中提取特征数据，并赋值给变量 X。X 是一个 150 x 4 的数组，表示 150 个样本的 4 个特征（花萼长度、花萼宽度、花瓣长度、花瓣宽度）。
3. y = iris.target：从 iris 数据集中提取目标标签，即每个样本所属的类别（0 表示 Setosa，1 表示 Versicolor，2 表示 Virginica）。这些标签将用于后续比较和评估聚类结果。
4. scaler = StandardScaler()：创建一个 StandardScaler 对象 scaler，用于对特征数据进行标准化。标准化是将数据转换为均值为 0，标准差为 1 的标准正态分布，以消除特征尺度不同对模型的影响。
5. X_scaled = scaler.fit_transform(X)：使用 scaler 对 X 中的数据进行标准化。fit_transform() 方法首先计算每个特征的均值和标准差，然后对数据进行标准化。标准化后的数据存储在 X_scaled 中，用于后续的聚类分析。

2.3 使用“肘部法则”选择 K 值

2.3.1 代码片段：

inertia = []
K_range = range(1, 11)
for k in K_range:
    kmeans = KMeans(n_clusters=k, random_state=42)
    kmeans.fit(X_scaled)
    inertia.append(kmeans.inertia_)

plt.figure(figsize=(8, 4))
plt.plot(K_range, inertia, marker='o')
plt.title('Elbow Method for Optimal K')
plt.xlabel('Number of clusters (K)')
plt.ylabel('Inertia')
plt.grid()
plt.show()

2.3.2 实现目的：

使用肘部法则通过观察簇内误差平方和 (inertia) 的变化，确定 K-Means 聚类中最合适的簇数量 KKK。

2.3.3 代码解释：

1. inertia = []：创建一个空列表 inertia，用于保存不同 K 值对应的簇内误差平方和 (inertia) 值。inertia 越小，表示簇内的数据点之间越紧密。
2. K_range = range(1, 11)：定义一个 K 值的范围，这里从 1 到 10。我们将尝试使用 1 到 10 个簇进行聚类，后续分析每个 K 值对应的聚类效果。
3. for k in K_range:：开始一个循环，遍历 K_range 中的每个 K 值，依次训练 K-Means 模型。
4. kmeans = KMeans(n_clusters=k, random_state=42)：为每个 K 值创建一个 K-Means 模型对象。n_clusters=k 表示簇的数量为当前的 K，random_state=42 是用于确保结果可复现的随机种子。
5. kmeans.fit(X_scaled)：使用 fit() 方法对标准化后的数据 X_scaled 进行训练，模型将找到 K 个簇的中心点，并将数据点分配到离其最近的中心点。
6. inertia.append(kmeans.inertia_)：训练完成后，提取当前模型的簇内误差平方和（kmeans.inertia_），并将其添加到 inertia 列表中。inertia_ 衡量了所有数据点到其最近的簇中心的距离和，是衡量聚类效果的指标。
7. plt.figure(figsize=(8, 4))：创建一个大小为 8x4 英寸的绘图窗口，用于绘制肘部图。
8. plt.plot(K_range, inertia, marker='o')：绘制 K 值与 inertia 之间的关系图。横轴是 K 值，纵轴是簇内误差平方和，marker='o' 表示在每个数据点上绘制圆形标记。
9. plt.title('Elbow Method for Optimal K')：设置图表的标题为“肘部法则选择最优 K”。
10. plt.xlabel('Number of clusters (K)')：设置横轴标签为“簇的数量 (K)”。
11. plt.ylabel('Inertia')：设置纵轴标签为“簇内误差平方和 (Inertia)”。
12. plt.grid()：启用网格显示，便于观察数据变化。
13. plt.show()：显示绘制的肘部法则图。通常在图中找到“肘部”位置（即曲线开始变平的点）可以帮助我们选择最优的 K 值。

2.4 使用选择后的 K 值初始化分类器

2.4.1 代码片段：

k = 3
kmeans = KMeans(n_clusters=k, random_state=42)
y_kmeans = kmeans.fit_predict(X_scaled)

 

2.4.2 实现目的：

根据肘部法则确定的最佳 K 值，初始化 K-Means 模型并进行聚类分析。

2.4.3 代码解释：

1. k = 3：根据之前的肘部法则图，选择最佳 K 值为 3，表示我们将数据分成 3 个簇。
2. kmeans = KMeans(n_clusters=k, random_state=42)：创建一个 K-Means 聚类模型，n_clusters=3 表示模型将数据划分为 3 个簇。random_state=42 确保结果的可复现性。
3. y_kmeans = kmeans.fit_predict(X_scaled)：使用 fit_predict() 方法对标准化后的数据 X_scaled 进行聚类：

• fit() 部分对数据进行训练，找到聚类中心。
• predict() 部分根据聚类结果为每个数据点分配一个簇标签。y_kmeans 保存了每个数据点的簇标签（0, 1, 2），表示该点所属的簇。

2.5 绘制聚类结果

2.5.1 代码片段：

plt.figure(figsize=(8, 6))
plt.scatter(X_scaled[y_kmeans == 0, 0], X_scaled[y_kmeans == 0, 1], s=100, c='red', label='Cluster 1')
plt.scatter(X_scaled[y_kmeans == 1, 0], X_scaled[y_kmeans == 1, 1], s=100, c='blue', label='Cluster 2')
plt.scatter(X_scaled[y_kmeans == 2, 0], X_scaled[y_kmeans == 2, 1], s=100, c='green', label='Cluster 3')

# 绘制聚类中心
plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], s=300, c='yellow', label='Centroids')
plt.title('K-means Clustering of Iris Data')
plt.xlabel('Feature 1 (scaled)')
plt.ylabel('Feature 2 (scaled)')
plt.legend()
plt.grid()
plt.show()

 

2.5.2 实现目的：

通过散点图显示每个簇的聚类结果，并展示 K-Means 模型中计算得到的聚类中心。

2.5.3 代码解释：

1. plt.figure(figsize=(8, 6))：创建一个大小为 8x6 英寸的图形窗口，准备绘制聚类结果。

2. plt.scatter(X_scaled[y_kmeans == 0, 0], X_scaled[y_kmeans == 0, 1], s=100, c='red', label='Cluster 1')：

   • 使用 plt.scatter() 绘制属于第 0 簇的数据点。
   • X_scaled[y_kmeans == 0, 0] 选取所有第 0 簇数据点的第一个特征（横坐标）。
   • X_scaled[y_kmeans == 0, 1] 选取所有第 0 簇数据点的第二个特征（纵坐标）。
   • s=100 设置数据点的大小为 100。
   • c='red' 设置数据点的颜色为红色，label='Cluster 1' 为该簇添加标签（将用于图例）。

3. plt.scatter(X_scaled[y_kmeans == 1, 0], X_scaled[y_kmeans == 1, 1], s=100, c='blue', label='Cluster 2')：

   • 同理，绘制属于第 1 簇的数据点，颜色为蓝色。

4. plt.scatter(X_scaled[y_kmeans == 2, 0], X_scaled[y_kmeans == 2, 1], s=100, c='green', label='Cluster 3')：

   • 同理，绘制属于第 2 簇的数据点，颜色为绿色。

5. plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], s=300, c='yellow', label='Centroids')：

   • 使用 plt.scatter() 绘制聚类中心点，大小设置为 300。
   • kmeans.cluster_centers_[:, 0] 表示所有簇中心的第一个特征值。
   • kmeans.cluster_centers_[:, 1] 表示所有簇中心的第二个特征值。
   • 颜色设置为黄色，标签为 Centroids，用于标识簇中心点。

6. plt.title('K-means Clustering of Iris Data')：为图表设置标题为“K-means 聚类鸢尾花数据”。

7. plt.xlabel('Feature 1 (scaled)')：设置横轴的标签为“特征 1（标准化后）”，代表第一个特征。

8. plt.ylabel('Feature 2 (scaled)')：设置纵轴的标签为“特征 2（标准化后）”，代表第二个特征。

9. plt.legend()：显示图例，说明不同颜色代表的簇。

10. plt.grid()：启用网格，方便观察数据的分布。

11. plt.show()：显示绘制的散点图，展示 3 个簇的数据点分布及其中心。

2.6 评价模型

2.6.1 代码片段：

import seaborn as sns
from sklearn.metrics import confusion_matrix

confusion_mat = confusion_matrix(y, y_kmeans)
plt.figure(figsize=(8, 6))
sns.heatmap(confusion_mat, annot=True, fmt='d', cmap='Blues',
            xticklabels=['Cluster 0', 'Cluster 1', 'Cluster 2'],
            yticklabels=['Class 0', 'Class 1', 'Class 2'])
plt.title('Confusion Matrix')
plt.xlabel('Predicted Clusters')
plt.ylabel('True Classes')
plt.show()

 

2.6.2 实现目的：

通过绘制混淆矩阵评估 K-Means 聚类的效果，比较聚类标签与真实标签之间的对应关系。

2.6.3 代码解释：

1. import seaborn as sns：导入 seaborn 库，seaborn 是一个高级数据可视化库，基于 matplotlib，提供了更美观和简洁的绘图接口。

2. from sklearn.metrics import confusion_matrix：从 sklearn.metrics 模块中导入 confusion_matrix 函数，用于计算混淆矩阵。混淆矩阵是用于评估分类模型性能的表格，行表示实际类别，列表示预测类别。

3. confusion_mat = confusion_matrix(y, y_kmeans)：

   • 使用 confusion_matrix() 函数生成混淆矩阵。
   • y 是真实类别标签，y_kmeans 是聚类后的标签。
   • 该函数将返回一个矩阵，矩阵中的值表示每个类别中真实标签与预测标签的匹配情况。

4. plt.figure(figsize=(8, 6))：创建一个大小为 8x6 英寸的图形窗口，准备绘制混淆矩阵。

5. sns.heatmap(confusion_mat, annot=True, fmt='d', cmap='Blues', xticklabels=['Cluster 0', 'Cluster 1', 'Cluster 2'], yticklabels=['Class 0', 'Class 1', 'Class 2'])：

   • 使用 sns.heatmap() 函数绘制混淆矩阵的热图。
   • confusion_mat 是混淆矩阵数据源。
   • annot=True 表示在每个单元格内显示具体的数值。
   • fmt='d' 指定数值以整数格式显示。
   • cmap='Blues' 指定热图的颜色映射为蓝色渐变。
   • xticklabels=['Cluster 0', 'Cluster 1', 'Cluster 2'] 和 yticklabels=['Class 0', 'Class 1', 'Class 2'] 分别为横轴和纵轴设置标签，表示聚类簇与真实类别的对应关系。

6. plt.title('Confusion Matrix')：设置图的标题为“混淆矩阵”。

7. plt.xlabel('Predicted Clusters')：设置横轴的标签为“预测簇”，表示 K-Means 聚类的结果。

8. plt.ylabel('True Classes')：设置纵轴的标签为“真实类别”，表示鸢尾花的实际类别。

9. plt.show()：显示绘制的热图。通过观察混淆矩阵，可以评估 K-Means 聚类的准确性，特别是它与真实类别标签的对应关系。

---

3.层次聚类对鸢尾花样本数据进行聚类

3.1 导入所需的模块

3.1.1 代码片段：

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from scipy.cluster.hierarchy import dendrogram, linkage
from sklearn.preprocessing import StandardScaler

 

3.1.2 实现目的：

导入必要的库，用于数据加载、标准化处理、层次聚类和可视化树状图。

3.1.3 代码解释：

1. import numpy as np：导入 numpy 库，numpy 是 Python 中的基础科学计算库，支持多维数组和矩阵运算，虽然在这段代码中没有直接使用，但它通常是机器学习数据处理的基础库。

2. import matplotlib.pyplot as plt：导入 matplotlib 库中的 pyplot 模块，用于绘制图形和数据可视化，并将其命名为 plt。

3. from sklearn.datasets import load_iris：从 sklearn.datasets 中导入 load_iris 函数，用于加载鸢尾花数据集，方便进行聚类分析。

4. from scipy.cluster.hierarchy import dendrogram, linkage：

   • dendrogram 用于绘制层次聚类的树状图（即“树形图”）。
   • linkage 是层次聚类的核心函数，它根据不同的聚类方法（如 ward、single、complete）计算聚类。

5. from sklearn.preprocessing import StandardScaler：从 sklearn.preprocessing 中导入 StandardScaler 类，用于对特征数据进行标准化，使其均值为 0，标准差为 1，消除特征之间的尺度差异。

3.2 加载鸢尾花数据并标准化

3.2.1 代码片段：

iris = load_iris()
data = iris.data

 

3.2.2 实现目的：

加载鸢尾花数据集，并提取特征数据用于后续的聚类操作。

3.2.3 代码解释：

1. iris = load_iris()：使用 load_iris() 函数加载鸢尾花数据集。鸢尾花数据集包含 150 个样本，每个样本有 4 个特征，并分为 3 类（Setosa、Versicolor、Virginica）。

2. data = iris.data：提取数据集中的特征数据，存储在 data 中。这个数组的大小是 (150, 4)，表示 150 个样本的 4 个特征：花萼长度、花萼宽度、花瓣长度、花瓣宽度。

3.3 数据标准化

3.3.1 代码片段：

scaler = StandardScaler()
data_std = scaler.fit_transform(data)

 

3.3.2 实现目的：

对特征数据进行标准化处理，使其均值为 0，标准差为 1，消除不同特征之间的尺度差异。

3.3.3 代码解释：

1. scaler = StandardScaler()：创建一个 StandardScaler 对象 scaler，用于后续的标准化处理。

2. data_std = scaler.fit_transform(data)：

   • fit_transform() 方法对数据进行标准化。首先计算特征的均值和标准差，然后将数据转换为标准化形式（即均值为 0，标准差为 1）。
   • data_std 是标准化后的数据，用于后续的层次聚类。

3.4 进行层次聚类

3.4.1 代码片段：

linked = linkage(data_std, 'ward')

 

3.4.2 实现目的：

使用层次聚类算法对标准化后的数据进行聚类。

3.4.3 代码解释：

1. linked = linkage(data_std, 'ward')：
   • linkage() 函数用于执行层次聚类，data_std 是经过标准化的数据。
   • 'ward' 是一种聚类方法，称为“Ward 最小方差法”，它通过最小化方差来选择合并簇的方式，具有良好的聚类效果，常用于层次聚类。
   • linked 是聚类结果，包含了一系列数据点之间的聚类关系，用于后续绘制树状图。

3.5 绘制树状图

3.5.1 代码片段：

plt.figure(figsize=(10, 7))
dendrogram(linked,
            orientation='top',
            labels=iris.target,
            distance_sort='descending',
            show_leaf_counts=True)

 

3.5.2 实现目的：

通过树状图展示层次聚类的结果，显示每个数据点的合并顺序和距离。

3.5.3 代码解释：

1. plt.figure(figsize=(10, 7))：创建一个大小为 10x7 英寸的图形窗口，准备绘制树状图。

2. dendrogram(linked, orientation='top', labels=iris.target, distance_sort='descending', show_leaf_counts=True)：

   • dendrogram() 函数用于绘制树状图：
     • linked 是之前通过 linkage() 计算得到的聚类关系结果。
     • orientation='top' 表示将树状图的树顶置于上方，分支从上到下展开。
     • labels=iris.target：使用真实的类别标签（iris.target）作为树叶节点的标签。
     • distance_sort='descending'：按距离降序排列聚类分支，距离越大的簇优先绘制。
     • show_leaf_counts=True：显示每个簇中的叶子节点数量，即该簇中的样本数量。

3.6 添加红色水平线和显示图像

3.6.1 代码片段：

plt.axhline(y=10, color='r', linestyle='--')
plt.show()

 

3.6.2 实现目的：

在树状图上添加一条水平的参考线，并显示最终的图像。

3.6.3 代码解释：

1. plt.axhline(y=10, color='r', linestyle='--')：

   • plt.axhline() 用于在图形中添加水平线。
   • y=10 指定水平线的纵坐标为 10，表示我们可以选择在此距离处切割树状图，确定簇的数量。
   • color='r' 指定水平线的颜色为红色，linestyle='--' 设置线条为虚线。

2. plt.show()：显示绘制好的树状图。通过观察树状图及其水平线，可以选择在不同的高度切割树状图，以确定不同的簇数量。

总结

• 这段代码实现了对鸢尾花数据集的层次聚类，并通过树状图可视化了数据点的合并过程。
• 树状图的水平线可以帮助我们在特定距离处进行切割，从而确定适合的聚类簇数。

---

4.密度聚类对鸢尾花样本数据进行聚类

4.1 导入所需的模块

4.1.1 代码片段：

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.cluster import DBSCAN
from sklearn.preprocessing import StandardScaler

 

4.1.2 实现目的：

导入必要的库，用于数据加载、标准化处理、执行 DBSCAN 密度聚类以及可视化聚类结果。

4.1.3 代码解释：

1. import numpy as np：导入 numpy 库，numpy 是用于科学计算的库，提供强大的多维数组处理能力，虽然在这段代码中没有直接使用，但 numpy 通常在数据处理和机器学习中被广泛应用。

2. import matplotlib.pyplot as plt：导入 matplotlib 库中的 pyplot 模块，用于绘制图形和数据可视化，命名为 plt。

3. from sklearn.datasets import load_iris：从 sklearn.datasets 中导入 load_iris 函数，用于加载经典的鸢尾花数据集。

4. from sklearn.cluster import DBSCAN：从 sklearn.cluster 中导入 DBSCAN 类，用于执行 DBSCAN 聚类算法。DBSCAN 是基于密度的聚类方法，能够识别任意形状的簇，并且对噪声和异常值具有很好的鲁棒性。

5. from sklearn.preprocessing import StandardScaler：从 sklearn.preprocessing 中导入 StandardScaler 类，用于标准化特征数据，消除特征尺度的影响。

4.2 加载鸢尾花数据并标准化

4.2.1 代码片段：

iris = load_iris()
data = iris.data

 

4.2.2 实现目的：

加载鸢尾花数据集，并提取特征数据用于后续的聚类分析。

4.2.3 代码解释：

1. iris = load_iris()：使用 load_iris() 函数加载鸢尾花数据集。该数据集包含 150 条样本，每条样本有 4 个特征（花萼长度、花萼宽度、花瓣长度、花瓣宽度）。

2. data = iris.data：从 iris 数据集中提取特征数据，并赋值给变量 data，这是一个 150 x 4 的数组，表示 150 个样本的 4 个特征。

---

4.3 数据标准化

4.3.1 代码片段：

scaler = StandardScaler()
data_std = scaler.fit_transform(data)

 

4.3.2 实现目的：

对特征数据进行标准化处理，使其均值为 0，标准差为 1，消除不同特征之间的尺度差异。

4.3.3 代码解释：

1. scaler = StandardScaler()：创建一个 StandardScaler 对象 scaler，用于对数据进行标准化处理。

2. data_std = scaler.fit_transform(data)：

   • 使用 fit_transform() 方法对 data 进行标准化。
   • fit() 部分计算每个特征的均值和标准差。
   • transform() 部分根据计算出的均值和标准差对数据进行缩放，结果存储在 data_std 中，这是标准化后的数据。

4.4 执行 DBSCAN 聚类

4.4.1 代码片段：

dbscan = DBSCAN(eps=1, min_samples=5)
labels = dbscan.fit_predict(data_std)

 

4.4.2 实现目的：

使用 DBSCAN 聚类算法对标准化后的数据进行聚类，并生成每个样本的聚类标签。

4.4.3 代码解释：

1.dbscan = DBSCAN(eps=1, min_samples=5)：

• 创建一个 DBSCAN 模型对象 dbscan，其中 eps=1 和 min_samples=5 是该模型的两个主要参数。
  • eps=1：定义邻域的半径，即两个样本如果在这个半径内就认为它们是密度相连的。
  • min_samples=5：定义一个点成为核心点所需的最小邻域内点数。如果某个点的邻域中至少有 5 个点（包括自己），则该点被视为核心点。
• DBSCAN 聚类算法通过计算样本之间的密度连接关系来识别簇，同时能够有效地处理噪声点。

2.labels = dbscan.fit_predict(data_std)：

• fit_predict() 方法对标准化后的数据 data_std 进行训练和预测。
• fit() 部分学习数据的密度分布，并确定每个样本的类别（即簇或噪声点）。
• predict() 部分返回每个样本的聚类标签，存储在 labels 中。聚类标签为整数：正整数表示簇编号，-1 表示噪声点。

4.5 绘制聚类结果

4.5.1 代码片段：

plt.scatter(data_std[:, 0], data_std[:, 1], c=labels, cmap='rainbow')
plt.title('DBSCAN Clustering')
plt.show()

 

4.5.2 实现目的：

通过二维散点图可视化 DBSCAN 聚类结果，展示每个样本所属的簇。

4.5.3 代码解释：

1.plt.scatter(data_std[:, 0], data_std[:, 1], c=labels, cmap='rainbow')：

• 使用 plt.scatter() 绘制二维散点图。
• data_std[:, 0] 表示标准化后数据的第一个特征（用于横坐标）。
• data_std[:, 1] 表示标准化后数据的第二个特征（用于纵坐标）。
• c=labels：设置每个样本的颜色，根据 labels（即聚类标签）来着色。
• cmap='rainbow'：使用 rainbow 颜色映射，将不同的聚类标签用不同的颜色表示。

2.plt.title('DBSCAN Clustering')：设置图表标题为“DBSCAN 聚类”。

3.plt.show()：显示绘制的散点图，展示聚类结果。每个不同颜色的点代表不同的簇，标签为 -1 的样本点将被标记为噪声点。

总结

• 这段代码使用 DBSCAN（基于密度的空间聚类算法）对鸢尾花数据集进行了聚类分析。
• DBSCAN 能识别任意形状的簇，并且自动处理噪声点（离群点），相比于 K-Means 这种必须指定簇数量的算法，DBSCAN 更加灵活。
• 聚类结果通过二维散点图展示，每个簇用不同颜色标识，噪声点也被自动识别出来。

---

5. 总体代码与结果分析

5.1 K-means 算法对鸢尾花（Iris）数据进行聚类

5.1.1 总体代码

# 第一步：导入所需的模块
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.cluster import KMeans
from sklearn.preprocessing import StandardScaler

# 第二步：加载并标准化鸢尾花数据集
iris = load_iris()
X = iris.data  # 特征数据
y = iris.target  # 实际标签（用于后续比较）
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

# 第三步：使用“肘部法则”选择K值
inertia = []
K_range = range(1, 11)
for k in K_range:
    kmeans = KMeans(n_clusters=k, random_state=42)
    kmeans.fit(X_scaled)
    inertia.append(kmeans.inertia_)

# 绘制肘部图
plt.figure(figsize=(8, 4))
plt.plot(K_range, inertia, marker='o')
plt.title('Elbow Method for Optimal K')
plt.xlabel('Number of clusters (K)')
plt.ylabel('Inertia')
plt.grid()
plt.show()

# 第四步：使用选择后的K值初始化分类器
k = 3
kmeans = KMeans(n_clusters=k, random_state=42)
y_kmeans = kmeans.fit_predict(X_scaled)

# 第五步：绘制聚类结果
plt.figure(figsize=(8, 6))
plt.scatter(X_scaled[y_kmeans == 0, 0], X_scaled[y_kmeans == 0, 1], s=100, c='red', label='Cluster 1')
plt.scatter(X_scaled[y_kmeans == 1, 0], X_scaled[y_kmeans == 1, 1], s=100, c='blue', label='Cluster 2')
plt.scatter(X_scaled[y_kmeans == 2, 0], X_scaled[y_kmeans == 2, 1], s=100, c='green', label='Cluster 3')

# 绘制聚类中心
plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], s=300, c='yellow', label='Centroids')
plt.title('K-means Clustering of Iris Data')
plt.xlabel('Feature 1 (scaled)')
plt.ylabel('Feature 2 (scaled)')
plt.legend()
plt.grid()
plt.show()

# 第六步：评价模型
import seaborn as sns
from sklearn.metrics import confusion_matrix

confusion_mat = confusion_matrix(y, y_kmeans)
plt.figure(figsize=(8, 6))
sns.heatmap(confusion_mat, annot=True, fmt='d', cmap='Blues',
            xticklabels=['Cluster 0', 'Cluster 1', 'Cluster 2'],
            yticklabels=['Class 0', 'Class 1', 'Class 2'])
plt.title('Confusion Matrix')
plt.xlabel('Predicted Clusters')
plt.ylabel('True Classes')
plt.show()

5.1.2 运行结果

5.1.3 结果分析

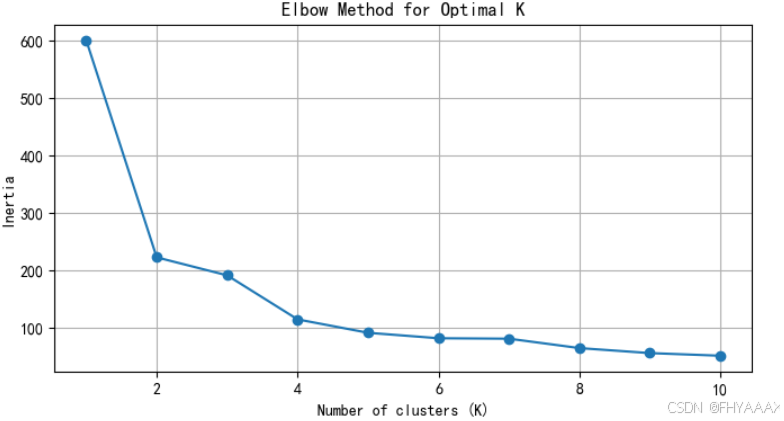
图 1：肘部法则（Elbow Method）

• 分析：
  • 图中显示了 K 值从 1 到 10 对应的簇内误差平方和（Inertia）。簇内误差平方和越低，说明簇内的数据点距离簇中心越近，聚类效果越好。
  • 从图中可以看到，在 K = 3 处，Inertia 下降明显变缓，形成一个肘部（Elbow）。这意味着选择 3 个簇是一个合适的选择，因为在此 K 值之后，增加簇的数量对簇内误差平方和的改善效果逐渐减小。
• 结论：根据肘部法则，K = 3 是最优的簇数量，因此选择 K=3 进行聚类。

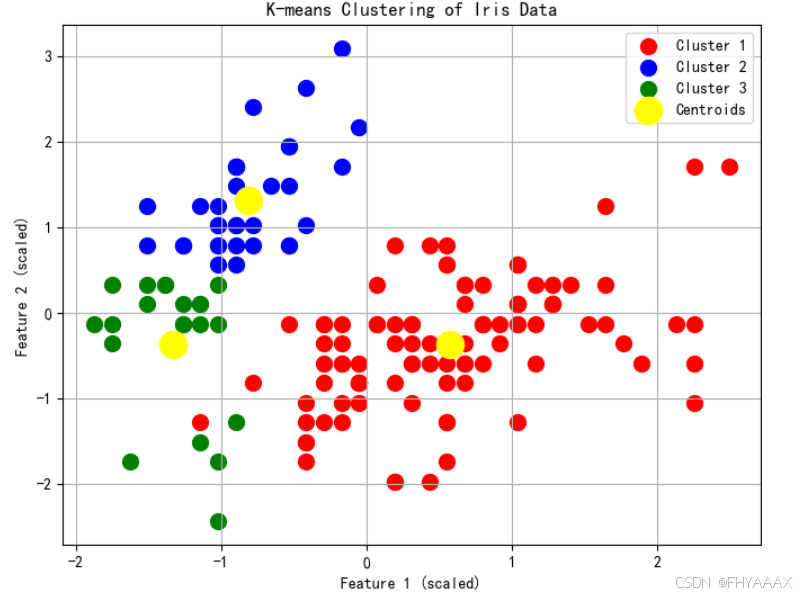
图 2：K-means 聚类结果散点图

• 分析：

  • 图中展示了鸢尾花数据集的前两个特征（经过标准化后）对应的聚类结果。每个点的颜色表示其所属的簇，红色、蓝色和绿色分别代表三个不同的簇，黄色圆点表示每个簇的聚类中心。
  • 从图中可以看出，K-means 算法将数据分成了三个簇，并且每个簇内的样本在图中表现为比较密集的簇形状。这表明 K-means 对鸢尾花数据集的特征进行了较好的划分。

• 结论：K-means 对数据的三个簇的分布进行清晰划分，尽管在某些地方（如红色和绿色簇的交界处）有一定的重叠，但整体表现较好。

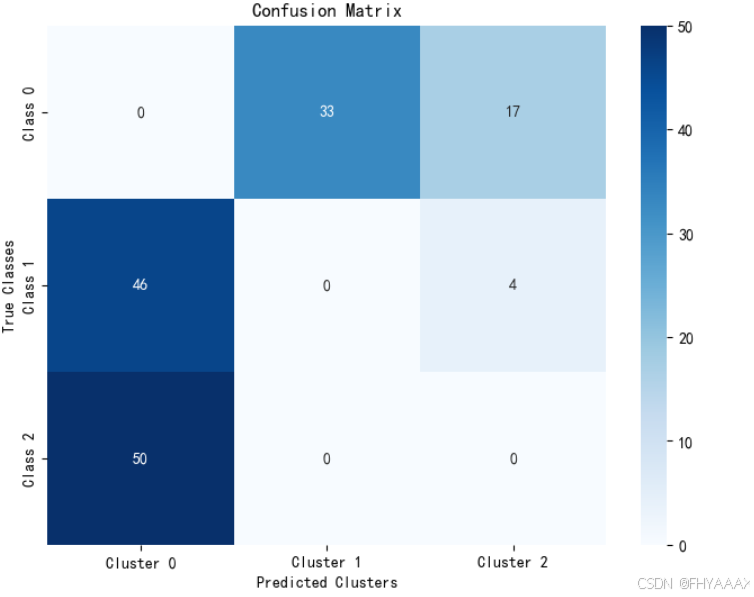
图 3：混淆矩阵（Confusion Matrix）

• 分析：

  • 混淆矩阵显示了聚类标签与真实类别标签的匹配情况。矩阵中的每个值表示真实类别和聚类标签的数量对比。
  • 横轴表示 K-means 聚类的预测结果，纵轴表示数据的真实类别。
  • 可以看到，Cluster 0 完全没有匹配到真实的 Class 0，而是大量匹配到了 Class 1 和 Class 2。这表明 K-means 对鸢尾花的第一类分类效果较差。
  • Cluster 1 主要匹配了 Class 0，但是也有一些样本错误匹配到 Cluster 2。
  • Cluster 2 主要对应的是 Class 2 的数据，分类效果相对较好。

• 结论：K-means 对鸢尾花数据集的聚类效果不完全准确，尤其是在分类 Class 1 和 Class 2 时有较大的偏差。尽管聚类效果大体符合预期，但在实际应用中可能需要更精细的参数调整或采用其他算法（如 DBSCAN 或层次聚类）来提高聚类效果。

5.2 层次聚类对鸢尾花样本数据进行聚类

5.2.1 总体代码

## 层次聚类

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from scipy.cluster.hierarchy import dendrogram, linkage
from sklearn.preprocessing import StandardScaler

# 加载鸢尾花数据
iris = load_iris()
data = iris.data

# 数据标准化
scaler = StandardScaler()
data_std = scaler.fit_transform(data)

# 使用层次聚类
linked = linkage(data_std, 'ward')

# 绘制树状图
plt.figure(figsize=(10, 7))
dendrogram(linked,
            orientation='top',
            labels=iris.target,
            distance_sort='descending',
            show_leaf_counts=True)
# 添加红色水平线
plt.axhline(y=10, color='r', linestyle='--')
plt.show()

5.2.2 运行结果

5.2.3 结果分析

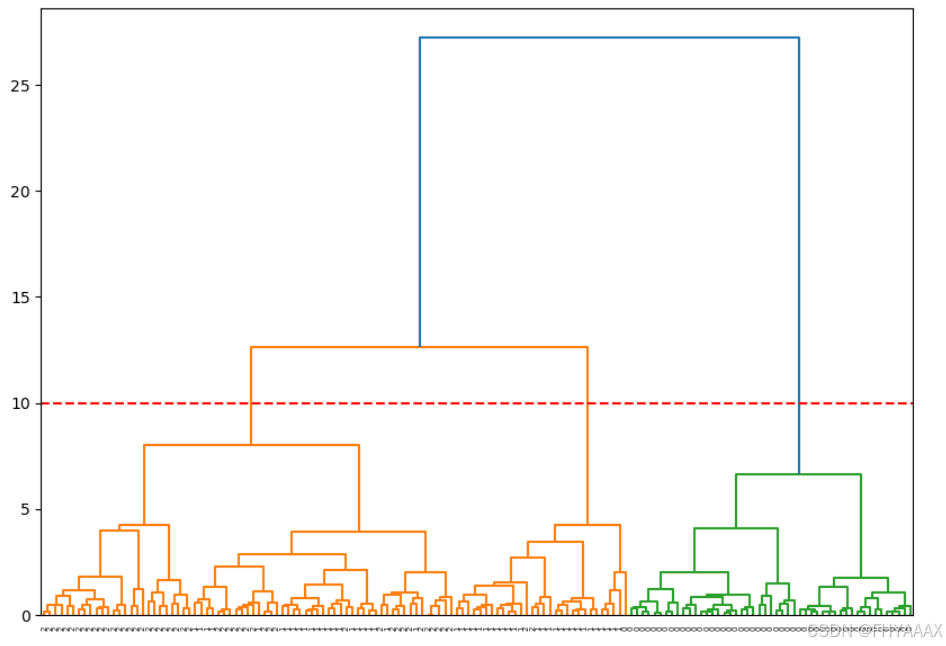
树状图分析：

1. 层次结构：

   • 树状图展示了层次聚类的过程。最底层的叶节点代表原始的数据点，逐步向上合并，最终所有数据点聚合为一个簇。
   • 水平线的高度表示簇合并时的距离。距离越大，说明合并的簇之间的相似性越低。

2. 红色虚线：

   • 红色的虚线（水平线）位于距离约为 10 的位置，表示在这个位置切割树状图，得到了几个不同的簇。
   • 从图中可以看出，在这个切割线处，树状图被分割成了 3 个主要簇。这个簇数量与前面 K-means 聚类中选出的 3 个簇一致，说明这个切割位置是合理的。

3. 簇的数量：

   • 根据树状图，可以直观地看到数据如何逐步合并为不同的簇。在红色虚线的切割位置，可以看到较清晰的三个聚类分支（颜色不同的区域），这与 K-means 的结果一致。

4. 聚类之间的距离：

   • 水平线的长度代表了簇之间的合并距离。较长的水平线表示在该处合并的簇之间距离较远，说明它们的相似性较低。
   • 从图中可以看到，最大的距离（最高的线）代表了最后一次合并的两个大簇，这说明这两个大簇之间的相似度相对较低。

总结：

• 从这张树状图中可以看出，层次聚类将数据逐渐聚合为簇，切割在红色虚线处时，我们得到了 3 个主要的簇。
• 这与之前使用肘部法则确定的 K 值（3 个簇）是一致的，进一步验证了数据的聚类结果。
• 如果你想要调整簇的数量，可以选择在树状图的其他高度切割，生成更多或更少的簇。

5.3 密度聚类对鸢尾花样本数据进行聚类

5.3.1 总体代码

## DBSCAN密度聚类

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.cluster import DBSCAN
from sklearn.preprocessing import StandardScaler

# 加载鸢尾花数据
iris = load_iris()
data = iris.data

# 数据标准化
scaler = StandardScaler()
data_std = scaler.fit_transform(data)

# 使用DBSCAN聚类
dbscan = DBSCAN(eps=1, min_samples=5)
labels = dbscan.fit_predict(data_std)

# 绘制聚类结果
plt.scatter(data_std[:, 0], data_std[:, 1], c=labels, cmap='rainbow')
plt.title('DBSCAN Clustering')
plt.show()

5.3.2 运行结果

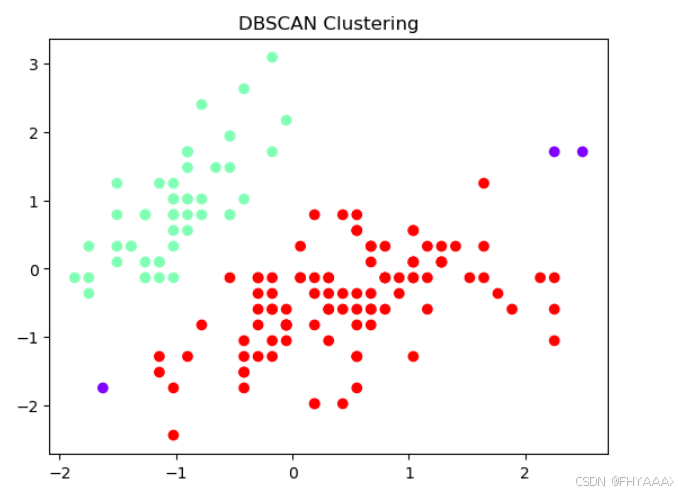
5.3.3 结果分析

图像分析：

1. 红色和青色的点：

   • 图中不同颜色的点代表不同的簇，DBSCAN 已经将数据分为了两个主要的簇：
     • 红色点表示其中一个簇。
     • 青色点表示另一个簇。
   • DBSCAN 能够识别形状不规则的簇，适合处理非球形簇，且不需要预先指定簇的数量（与 K-means 不同）。

2. 紫色的点：

   • 紫色的点代表 噪声点（离群点）。DBSCAN 能够识别数据中的噪声，噪声点是那些无法归入任何簇的数据点。
   • 这些点被 DBSCAN 标记为 -1（噪声标签），因为它们在定义的密度范围内没有足够的邻居点（即它们没有足够高的密度，或不在任何簇的核心区域内）。

3. 密度参数的影响：

   • DBSCAN 的两个关键参数是 eps（邻域半径）和 min_samples（最小样本数）。这张图是基于设置的 eps=1 和 min_samples=5 得到的结果。
   • 这两个参数的选择非常重要，它们决定了哪些点会被认为是核心点、边界点或者噪声点。你可以调整这两个参数来尝试不同的聚类效果。

聚类效果评价：

1. 簇的形状：

   • DBSCAN 在此数据集上识别出了两个簇，且这两个簇的形状不规则，与之前 K-means 划分的球形簇不同。这展示了 DBSCAN 的强大之处，它能够发现任意形状的簇。

2. 噪声点的检测：

   • 在图中可以看到有一些数据点（紫色的点）被识别为噪声点。这些点可能是异常点，或者在当前参数下无法归入任何簇。
   • DBSCAN 能够自然处理这种情况，而不像 K-means 那样必须将每个点分配到某个簇。

总结：

• DBSCAN 成功将数据集分成了两个主要簇，并识别了一些噪声点。
• 它适用于这种含有异常点或者非规则形状簇的数据集，不需要事先确定簇的数量。
• 如果你想优化结果，可以通过调整 eps 和 min_samples 参数来改善聚类表现。