树型结构
树的概念
在正式学习二叉树之前,我们先来了解一下:数据结构中什么是树型结构。我们前面学习的顺序表、链表、栈、队列这些都是线性结构的。
树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看 起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。
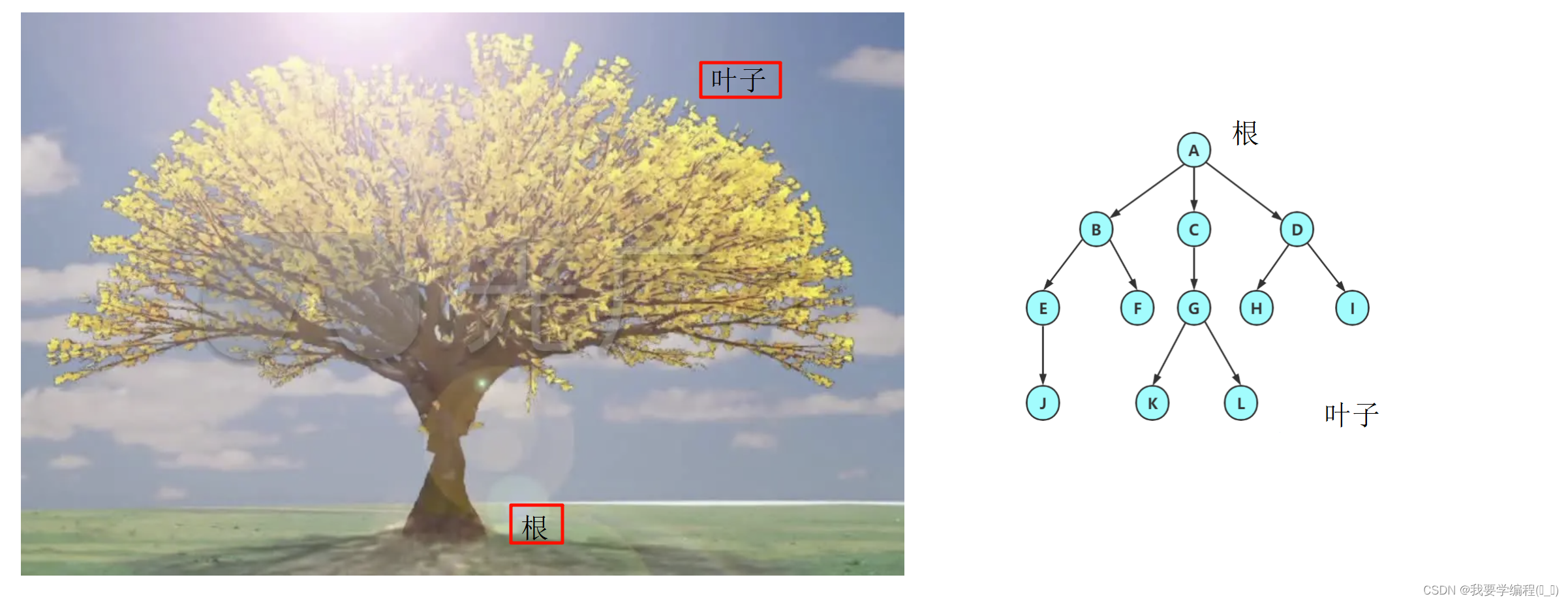
左边是大自然中正常的树,右边是数据结构中的树。
数据结构中的树具有以下的特点:
1、有一个特殊的结点,称为根结点,根结点没有前驱结点。
2、除根结点外,其余结点被分成M(M > 0)个互不相交的集合T1、T2、......、Tm,其中每一个集合Ti (1 <= i <= m) 又是一棵与树类似的子树。每棵子树的根结点有且只有一个前驱,可以有0个或多个后继。总结就是一句话:子树与子树之间不能有相交的部分,相交了就不能称之为树了。
3、树是递归定义的。
4、除了根结点外,每个结点有且仅有一个父结点。
5、一棵N个结点的树有N-1条边。
与树的有关概念
重点掌握:
结点的度:一个结点所含的子树的个数,也就是一个节点多少条边。
树的度:因为树有多个结点,因此树结点就是整个树中 所有 结点的度 的最大值。
叶子结点或终端结点:度为0的点,也就是没有边的点。
双亲结点或父结点:若一个结点A含有子结点B,则称该节点A为父结点。
孩子结点或子结点:若一个结点A含有子结点B,则称该节点B为子结点。
根结点:一棵树中,没有 双亲结点 的 结点,就是最上面的那个结点。
结点的层次:从根开始定义起,根为第1层,根的子结点为第2层,以此类推。
树的高度或深度:树中结点的最大层次,其实就是从根节点到叶子结点之间的最大值。
了解即可:
非终端结点或分支结点:度不为0的结点。
兄弟结点:具有相同 父结点 的 结点 互称 为兄弟结点。
堂兄弟结点:双亲在同一层的结点,它们的子结点 互为 堂兄结点。
结点的祖先:从根到该结点所经分支上的所有结点,都称为该结点的祖先。
子孙:以某结点为根的子树中任一结点都称为该结点的子孙。
森林:只要是能构成树的结点,就可以称为森林。例如:一颗树有一个节点,那么构成这棵树的这个结点也可以称为森林。
树的表示形式
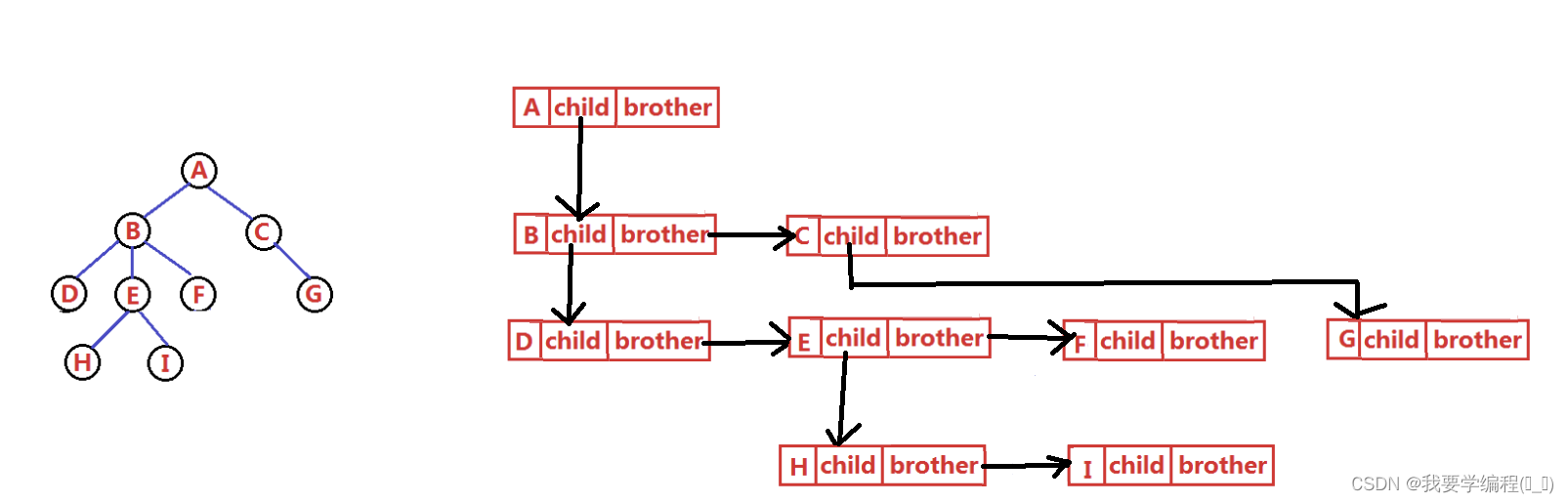
树的结构相对线性表就比较复杂了,要存储表示起来就比较麻烦,实际中树有很多种表示方式,如:双亲表示法, 孩子表示法、孩子双亲表示法、孩子兄弟表示法等等。我们这里就简单的了解其中最常用的孩子兄弟表示法。 顾名思义:这个节点中可以储存其孩子和兄弟:
class Node {
int value; // 树中存储的数据
Node firstChild; // 第一个孩子引用
Node nextBrother; // 下一个兄弟引用
}如下图所示:
树的应用
我们电脑的磁盘目录就是用的树这种数据结构。
二叉树
概念
二叉树是 结点的 一个有限集合,该集合: 1. 要么为空,即没有一个节点 2. 要么是由一个根节点加上两棵别称为左子树和右子树的二叉树组成。就像下面这样:
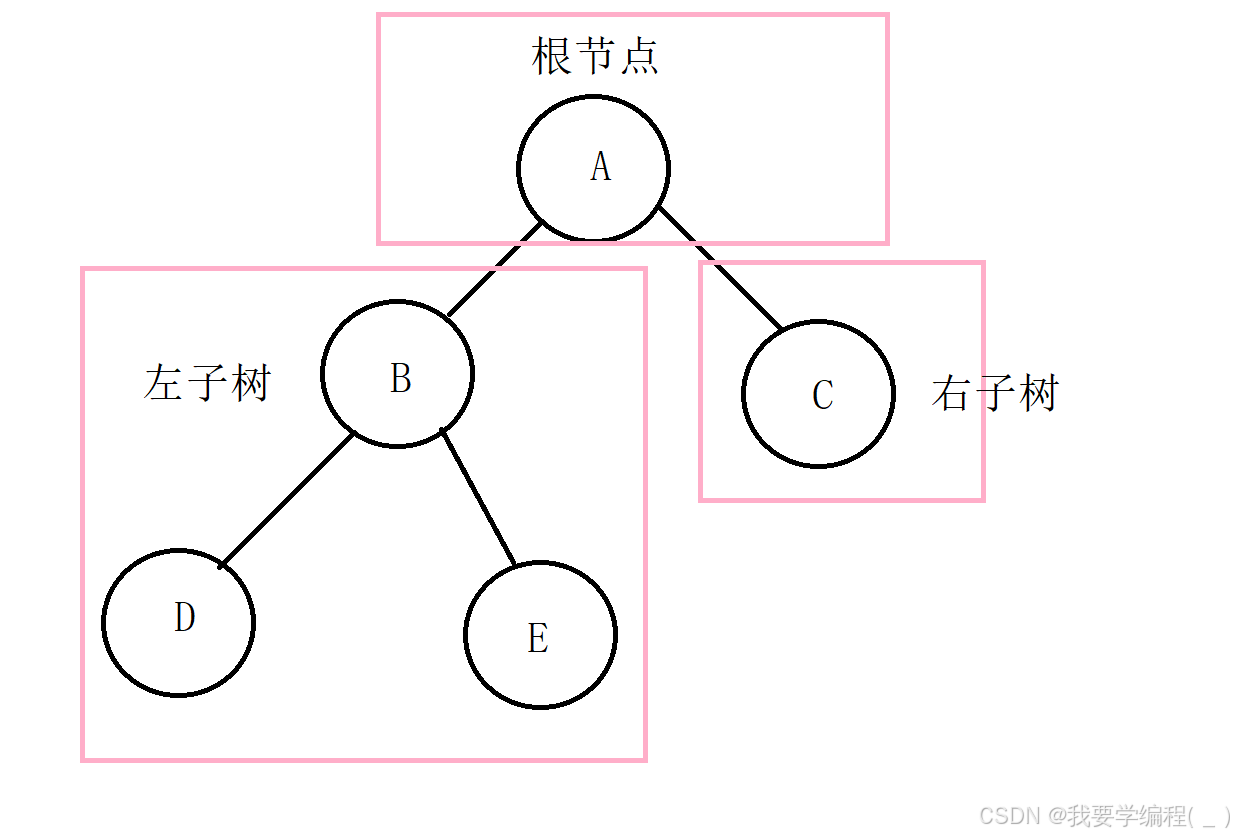
从上图可以看出:
1. 二叉树不存在度大于2的结点。(结点的度是指一个结点所含的边的条数,也就是子树的个数)
2. 二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树。
对于任意的二叉树都是由以下几种情况复合而成的:
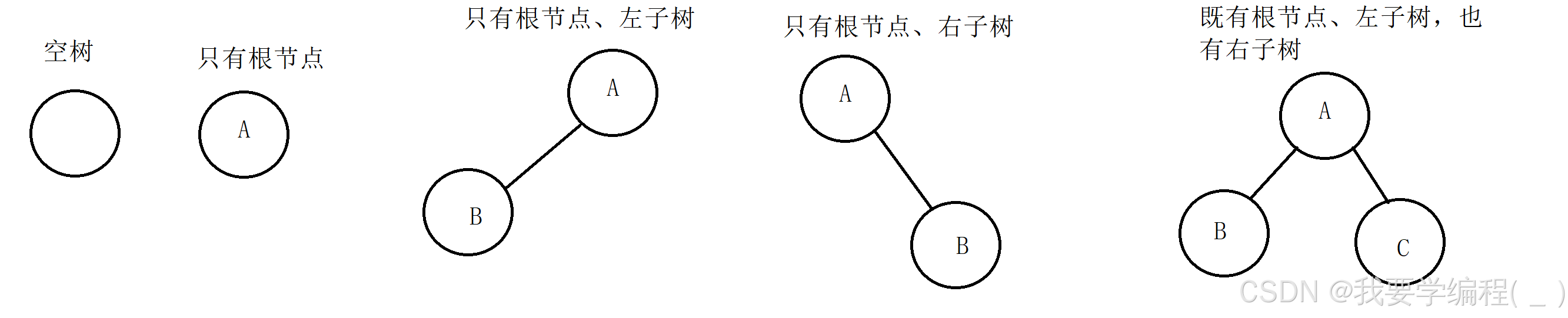
两种特殊的二叉树
满二叉树:一棵二叉树每层的结点数都达到最大值,则这棵二叉树就是满二叉树,如果一棵 二叉树的层数为K,且结点总数是 2^k -1,则它就是满二叉树。例:
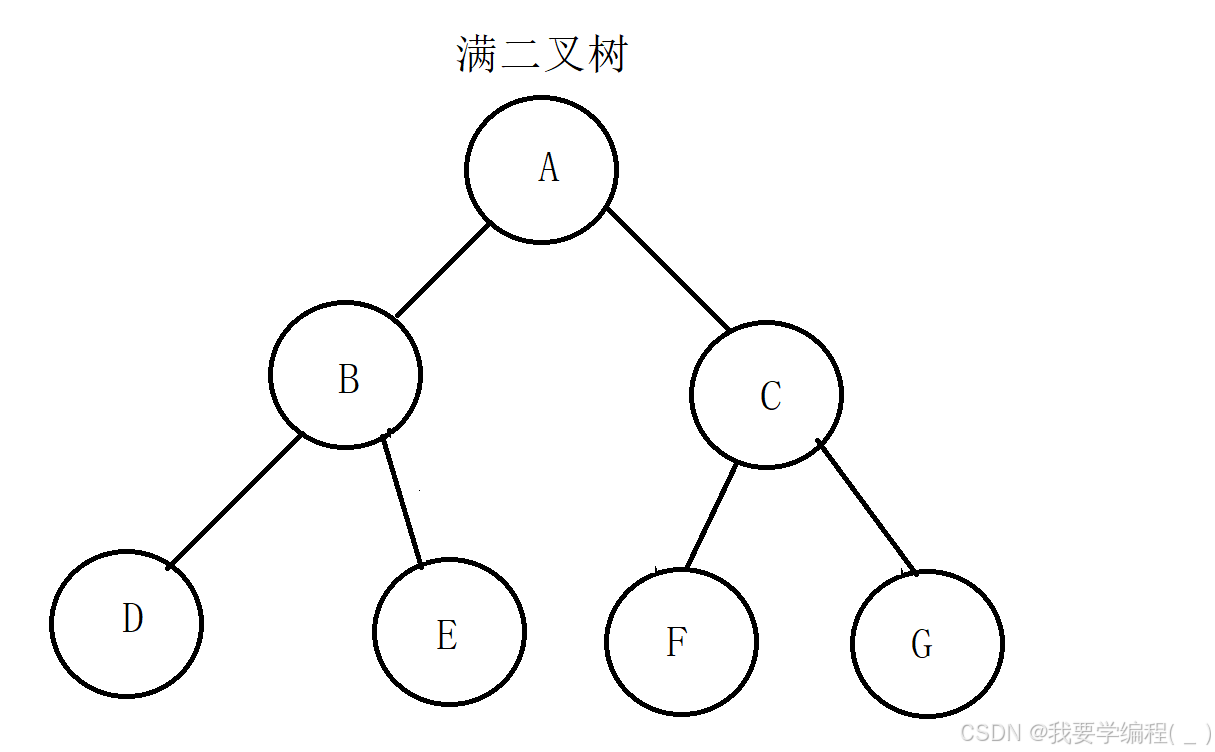
当然这里可能会有一个误区:有小伙伴可能会认为:只要一棵二叉树 只存在度为0 和 度为2 的结点,那么这棵树就是满二叉树。这个观点是不正确的。如下图所示:

完全二叉树:一棵二叉树的所有结点都是从上到下、从左到右依次存在的,这样的二叉树就被称为完全二叉树。例:
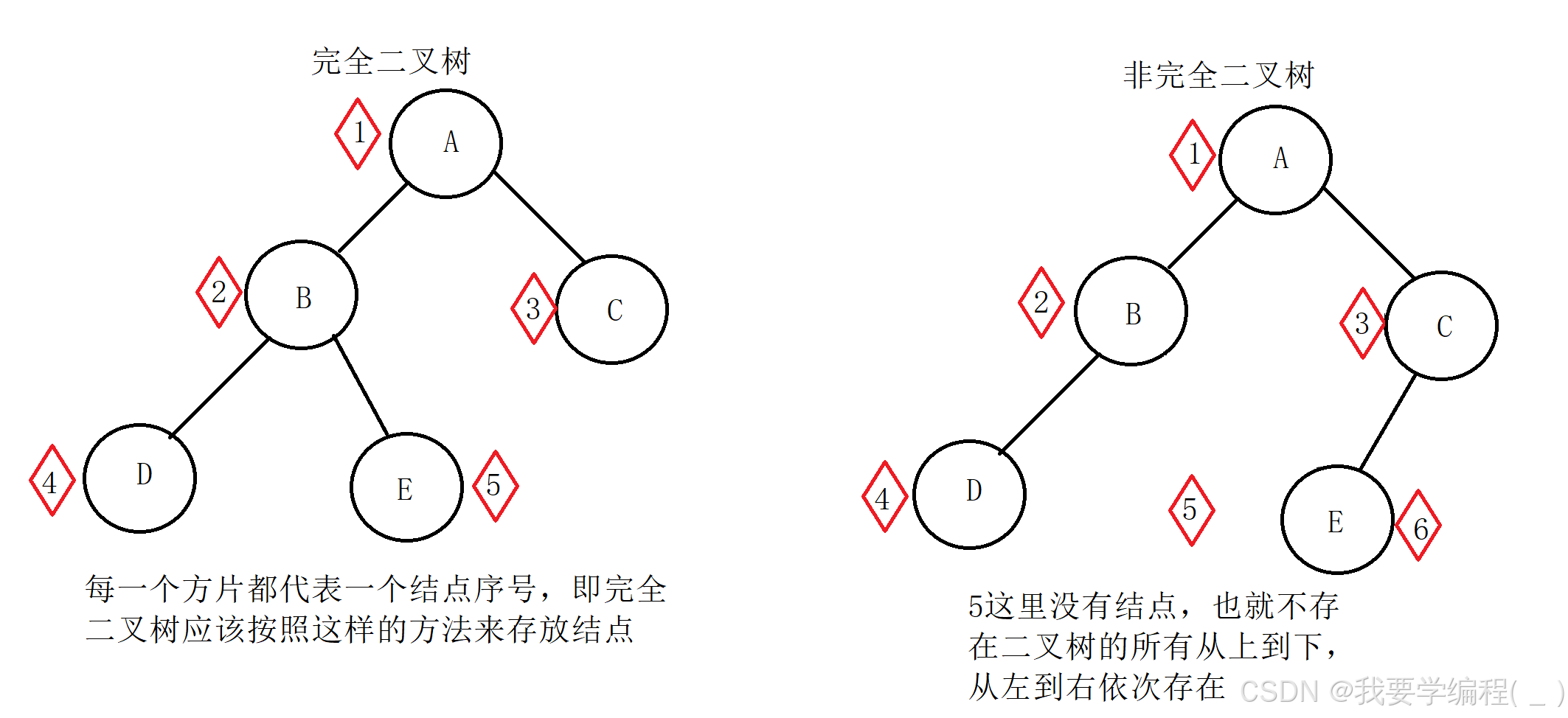
注意:满二叉树也是一种完全二叉树。因为满二叉树也满足完全二叉树的定义。
二叉树的性质
1. 若规定根结点的层数为1,则一棵非空二叉树的第i层上最多有 2^(i-1) (i>0)个结点。例:
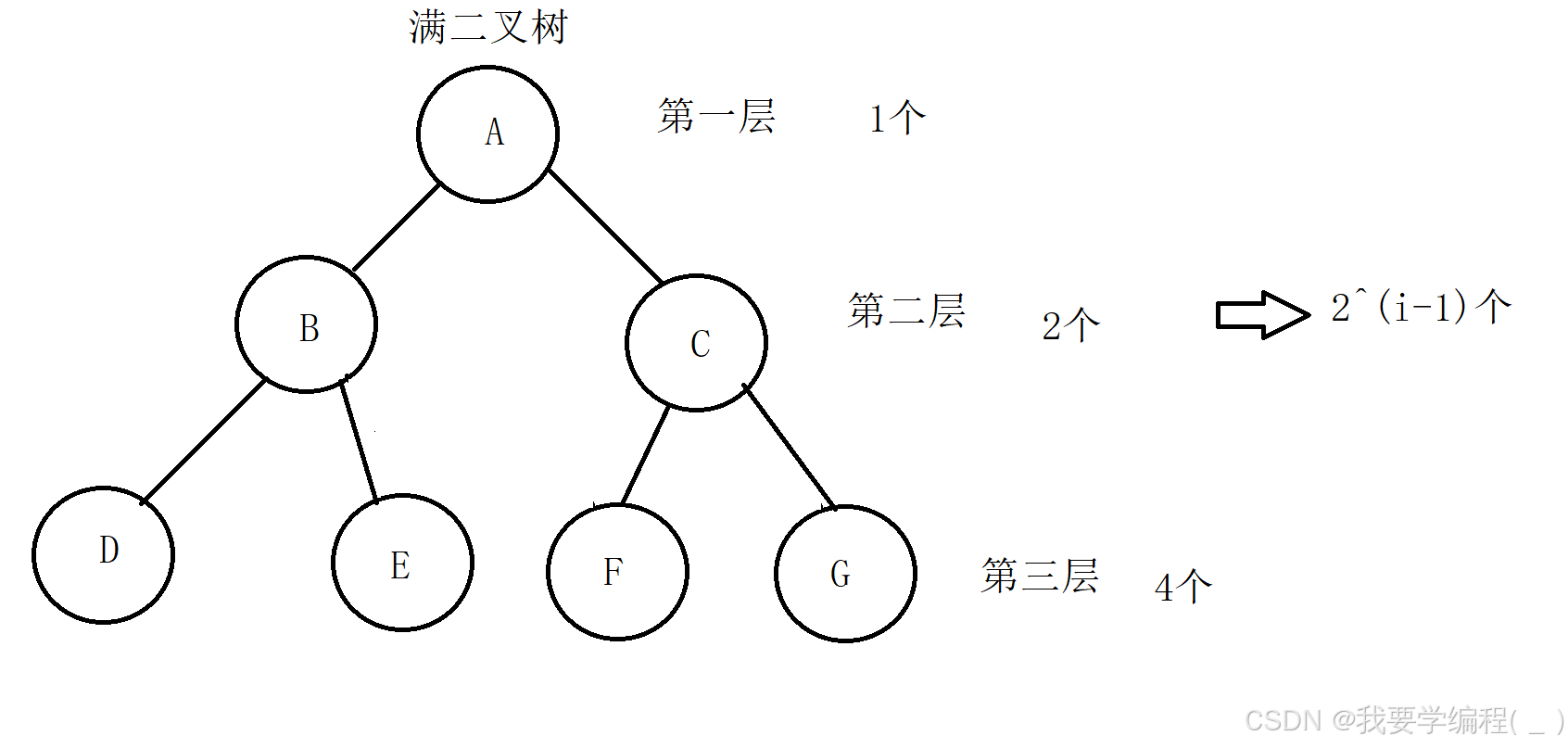
2. 若规定只有根结点的二叉树的深度为1(也就是说根是第1层),则深度为K的二叉树的最大结点数是 (2^k) - 1(k>=0) 。这里求的总的结点个数,也可以通过上图看出。其实也就是一个等比数列的求和问题。
3. 具有n个结点的完全二叉树的深度k为 log2 (N+1)(log以2为底,N+1的对数) 向上取整。这个公式就是根据 第2点 反推出来的。下面会有例子证明这个向上取整的意思。

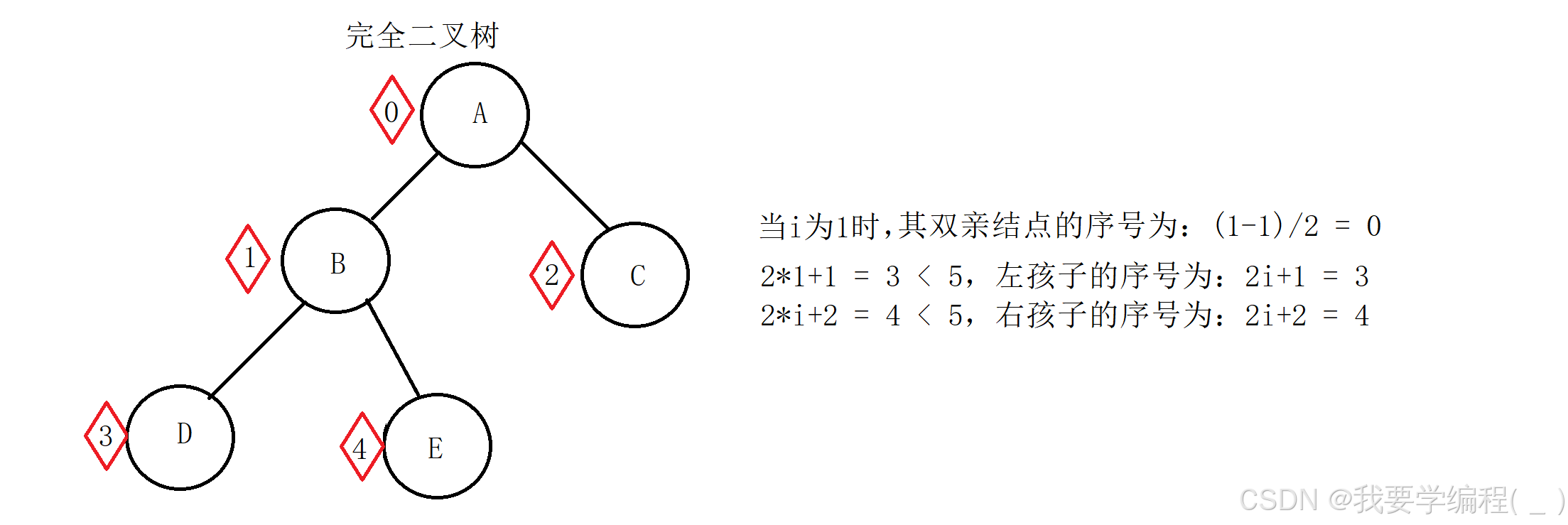
4. 对于具有n个结点的完全二叉树,如果按照从上至下从左至右的顺序对所有节点从0开始编号,则对于序号为 i 的结点有:
若 i > 0,双亲(父亲结点)序号:(i-1)/2;i=0,i 为根结点编号,无双亲结点。
若2i+1 < n,则左孩子序号为:2i + 1;2i+1 >= n,则无左孩子。
若2i+2 < n,则右孩子序号为:2i + 2;2i+2 >= n,则无右孩子。
例如:
5. 对于任意一棵二叉树,如果其叶子节点的个数为 n0,度为2的节点个数为 n2 ,则n0 = n2 + 1。即:度为0的结点的个数(叶子结点) 等于 度为2的结点的个数+1
推导过程如下:

有关二叉树的性质的练习
1.某二叉树共有399个结点,其中有199个度为2的结点,则该二叉树中的叶子结点数为()
A 不存在这样的二叉树 B 200 C 198 D 199答案:B
解析:根据前面的结论:叶子结点的个数比度为2的结点的个数多1,可知为200,选B
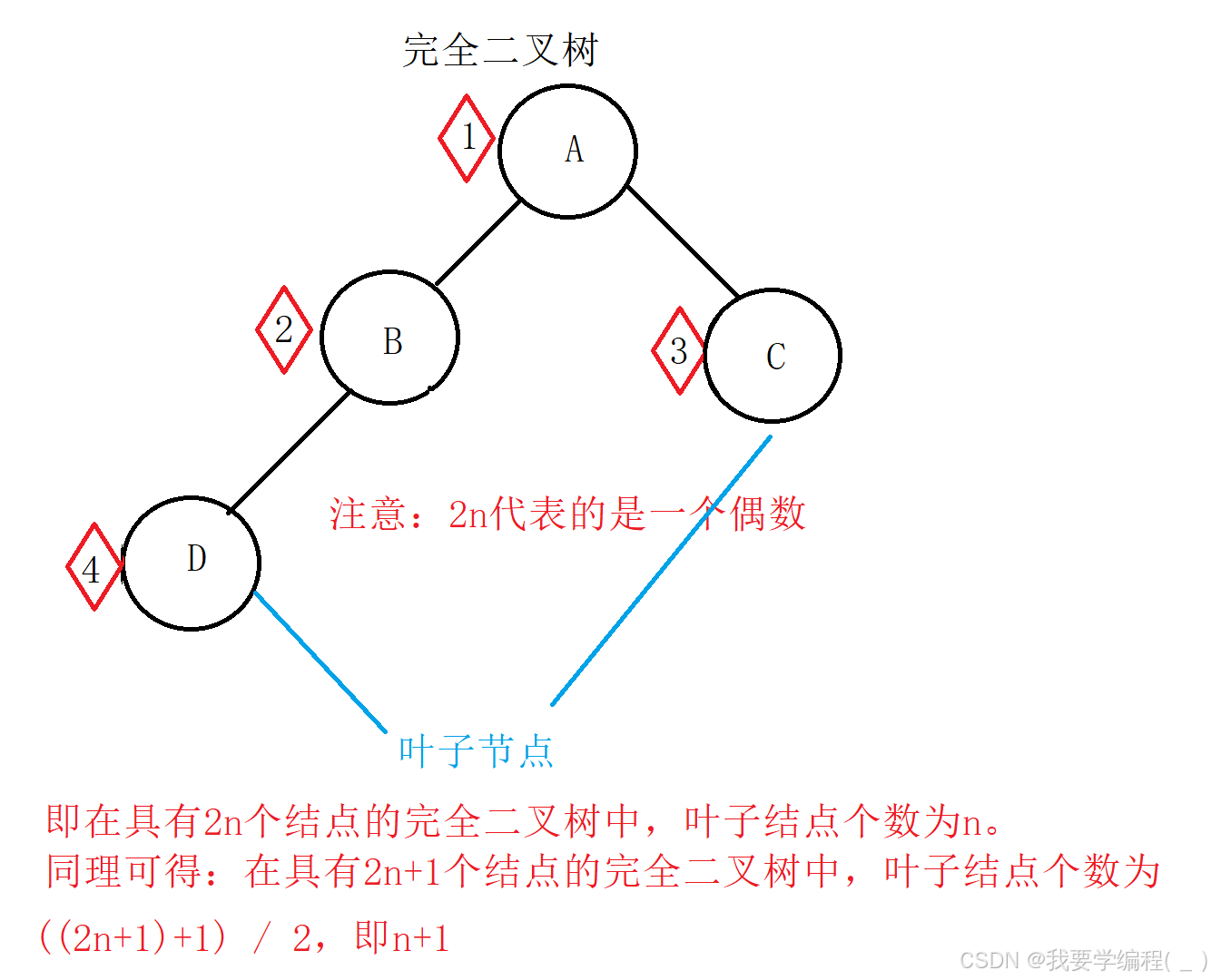
2.在具有2n个结点的完全二叉树中,叶子结点个数为()
A n个 B (n+1)个 C (n-1)个 D (n/2)个答案:A
解析:图解法:
3.一个具有767个节点的完全二叉树,其叶子节点个数为()
A 383个 B 384个 C 385个 D 386个答案:B
解析:由上图可知,叶子结点的个数为 (767+1) / 2 = 384。选B。
4.一棵完全二叉树的节点数为531个,那么这棵树的高度为()
A.11 B.10 C.8 D.12答案:B
解析:log2 (531+1) > log2 512 = 9,向上取整就是10.
二叉树的存储
二叉树的存储结构分为:顺序存储和类似于链表的链式存储。
顺序存储在后面学习。
二叉树的链式存储是通过一个一个的节点引用起来的,常见的表示方式有二叉和三叉表示方式,具体如下:
// 孩子表示法
class Node {
int val; // 数据域
Node left; // 左孩子的引用,常常代表左孩子为根的整棵左子树
Node right; // 右孩子的引用,常常代表右孩子为根的整棵右子树
}
// 孩子双亲表示法
class Node {
int val; // 数据域
Node left; // 左孩子的引用,常常代表左孩子为根的整棵左子树
Node right; // 右孩子的引用,常常代表右孩子为根的整棵右子树
Node parent; // 当前节点的根节点
}孩子双亲表示法后序在平衡树位置介绍,本文采用孩子表示法来构建二叉树。
二叉树的遍历
二叉树有四种遍历方式:前序遍历、中序遍历、后序遍历、层次遍历。
前序遍历(先序遍历):就是先遍历根结点,再遍历左子树,最后再遍历右子树。
中序遍历:就是先遍历左子树,再遍历根结点,最后再遍历右子树。
后序遍历:就是先遍历左子树,再遍历右子树,最后再遍历根结点。
层序遍历:就是从上到下、从左到右依次遍历根结点。
根据上述概念,我们不难发现遍历根节点的顺序不同,遍历方式也就有了区别。
先遍历根结点就是前序遍历。不管是哪个遍历,一定是左子树在前,右子树在后。
二叉树遍历的练习
1、下面二叉树的四种遍历方式:
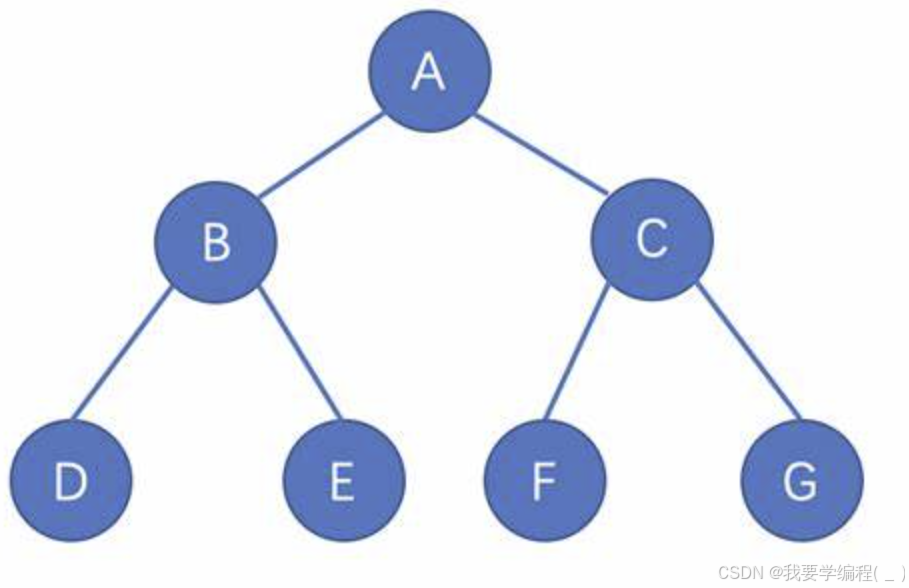
先序遍历:根->左子树->右子树。打印结果:A->B->D->E->C->F->G
中序遍历:左子树->根->右子树。打印结果:D->B->E->A->F->C->G
后序遍历:左子树->右子树->根。打印结果:D->E->B->F->G->C->A
层序遍历:从上到下、从左到右,依次打印根结点。打印结果:A->B->C->D->E->F->G
根据上面的遍历结果,我们也可以发现一些关于遍历的性质:
1、先序遍历一定会先打印整棵树的根结点,其次再是打印左子树的根节点,依次遍历下去。而后续遍历往往与其相反,最后才打印整棵树的根结点。
2、中序遍历的根结点一定是在中间的,通过后续遍历或者前序遍历确定了根结点之后,在根结点左边的就是根结点的左子树,在根结点右边的就是根结点的右子树。
有了上面这些性质,我们就可以更加迅速的把下面的题目给写完了。
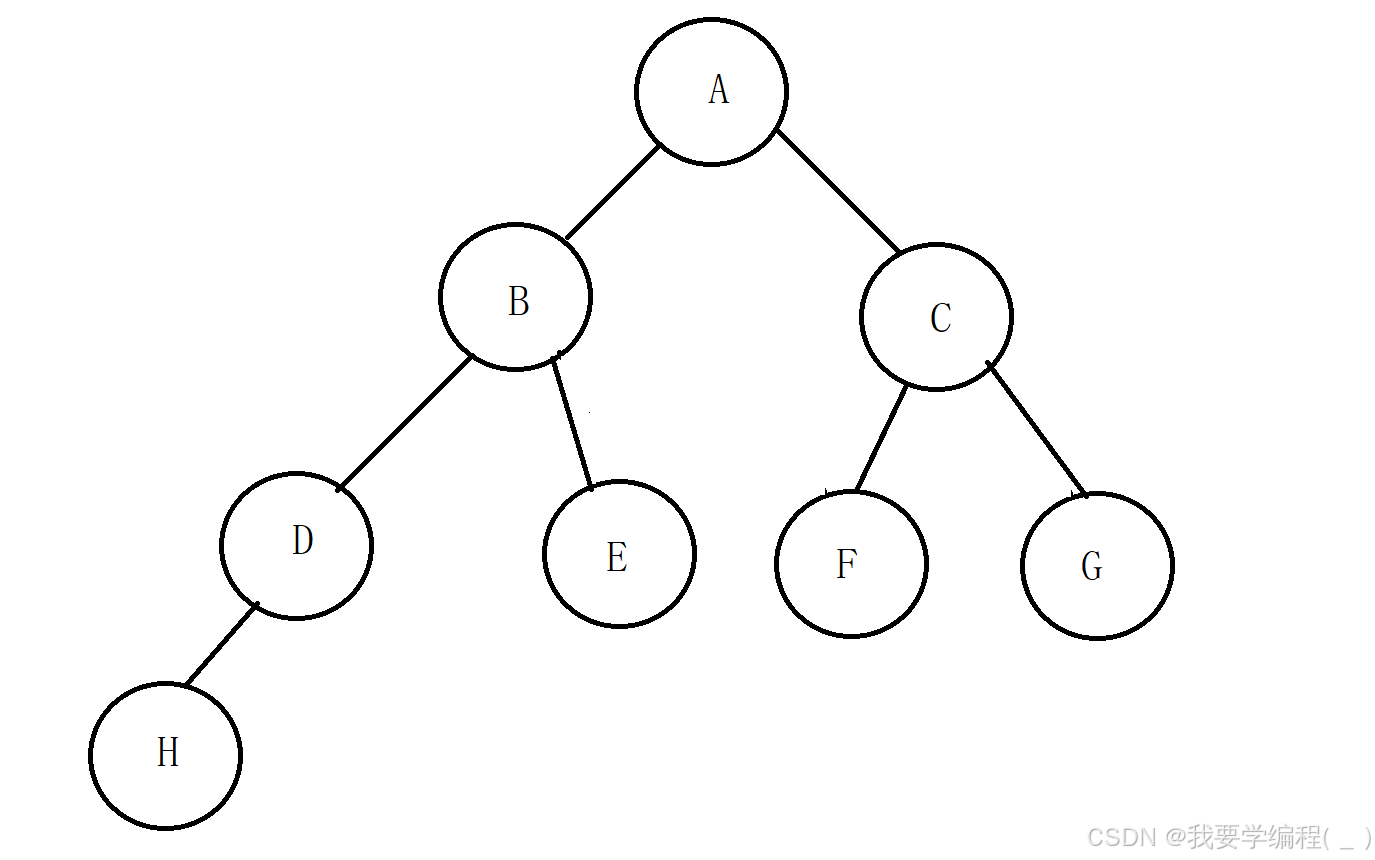
2、某完全二叉树按层次输出(同一层从左到右)的序列为 ABCDEFGH 。该完全二叉树的前序序列为()
A: ABDHECFG B: ABCDEFGH C: HDBEAFCG D: HDEBFGCA
答案:A
解析:
由题意知:该树为完全二叉树,因此就可以确定该树的图形如上所示:
前序遍历:A->B->D->H->E->C->F->G
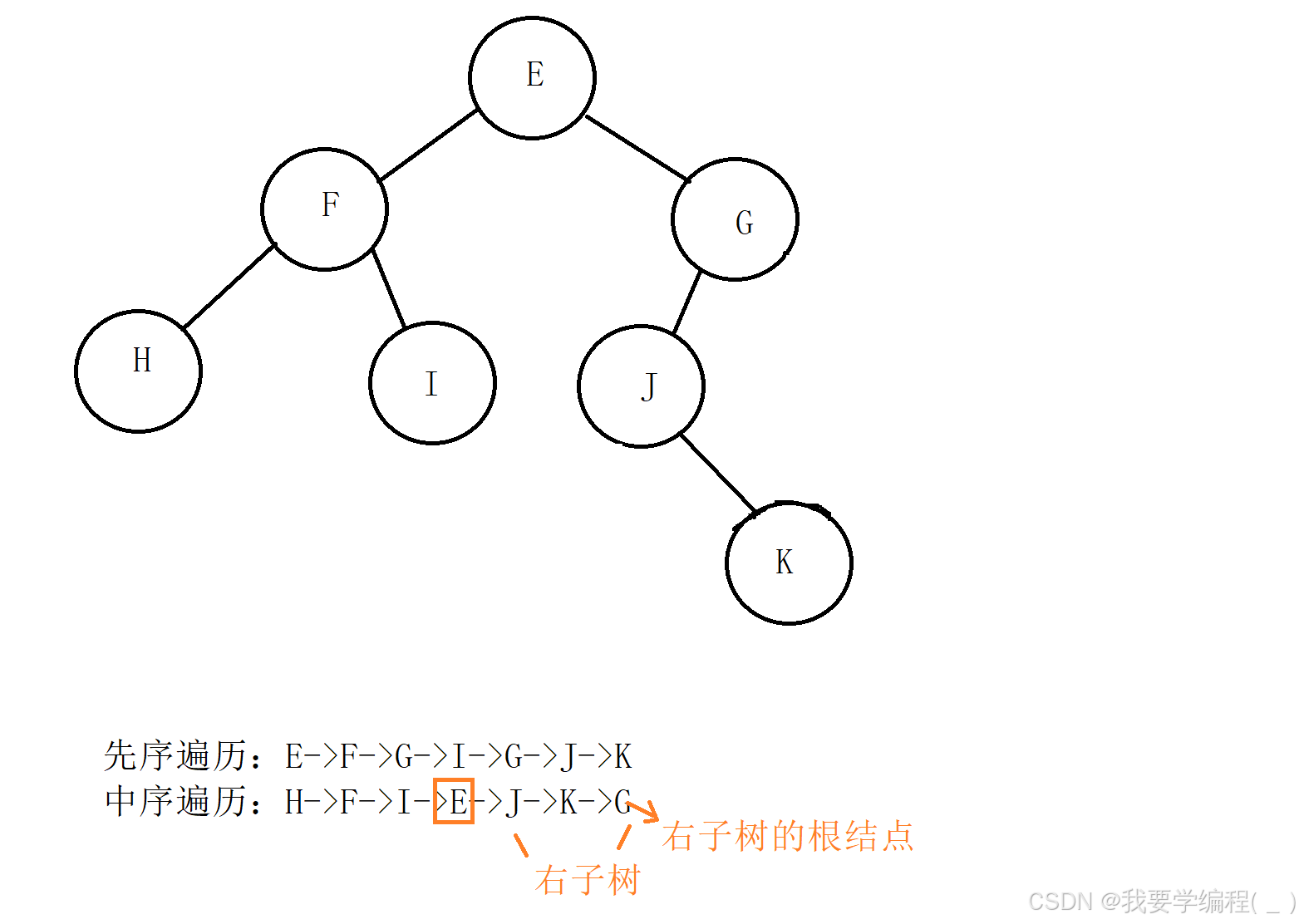
2、二叉树的先序遍历和中序遍历如下:先序遍历:EFHIGJK;中序遍历:HFIEJKG.则二叉树根结点为()
A: E B: F C: G D: H
答案:A
解析:根据先序遍历可以确定整棵树的根结点,即E,又因为中序遍历已知根结点,可以确定整棵树的左子树和右子树,则这棵树的图形如下所示:
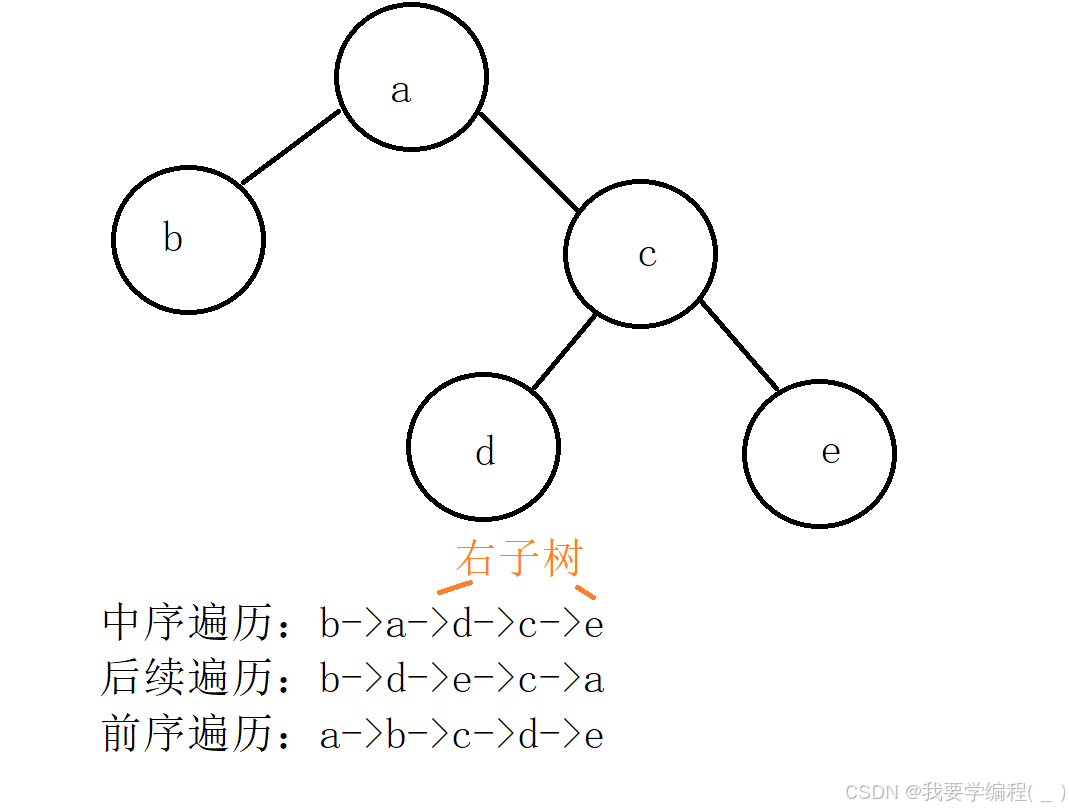
3、设一棵二叉树的中序遍历序列:badce,后序遍历序列:bdeca,则二叉树前序遍历序列为()
A: adbce B: decab C: debac D: abcde
答案:D
解析:根据后序遍历可以确定整棵树的根结点,即a,又因为中序遍历已知根结点,可以确定整棵树的左子树和右子树,则这棵树的图形如下所示:
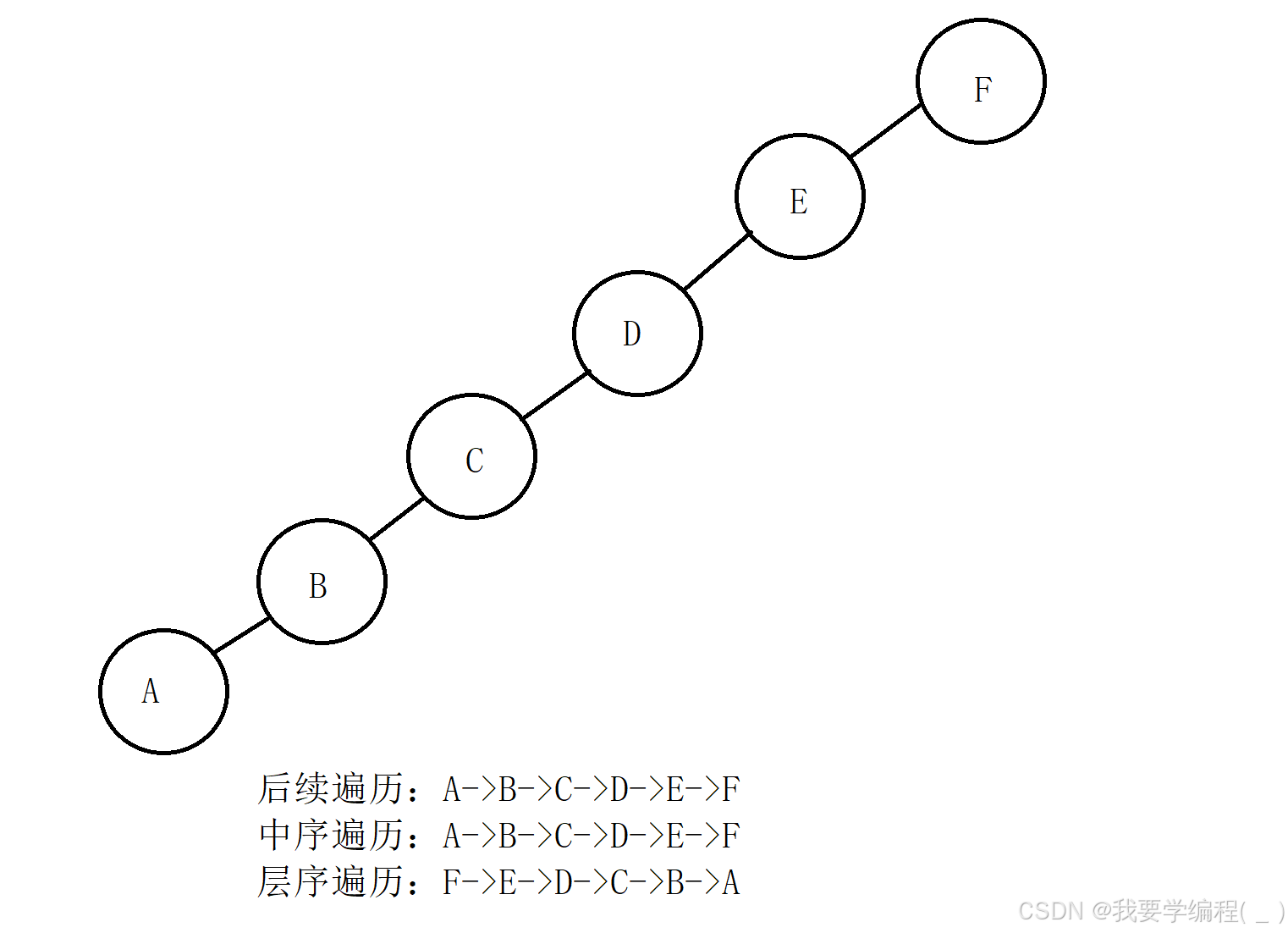
4、某二叉树的后序遍历序列与中序遍历序列相同,均为 ABCDEF ,则按层次输出(同一层从左到右)的序列为()
A: FEDCBA B: CBAFED C: DEFCBA D: ABCDEF
答案:A
解析:根据后序遍历可以确定整棵树的根结点,即F,又因为中序遍历已知根结点,可以确定整棵树的左子树和右子树,则这棵树的图形如下所示:
好啦!本期 数据结构之初始二叉树(1)的学习之旅就到此结束啦!本期文章主要是了解一些概念与遍历的方式,下一期我们就会开始代码的练习了。我们下一期再一起学习吧!