前言：哈喽小伙伴们，紧随上篇文章树的讲解，我们这篇文章开始进行二叉树的讲解。

先来看二叉树的一种特殊形式——堆。

一.什么是堆

我们已经了解到，二叉树有顺序存储和链式存储两种方式。其中顺序存储比较特殊，它用数组来作为架构，这就要求树的各个节点之间必须是连续且有序，这样一来只有完全二叉树才符合条件，所以我们将顺序存储的二叉树另起一个新名字——堆。

---

二.堆的概念

堆既然作为从二叉树独立出来的一个新的数据结构，自然要有它自己的特性：

• 堆中的某个节点的值总是不大于或不小于其父节点的值。
• 堆总是一棵完全二叉树。
• 堆按照从上到下，从左到右的顺序依次在数组中排列。

如何理解第一个特性呢？？？来看下图：

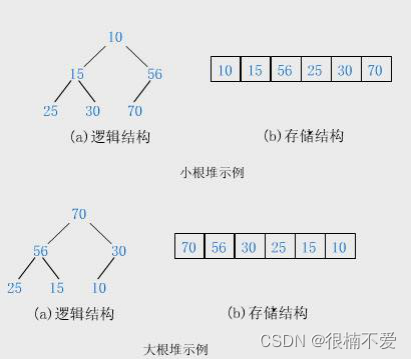
• 如果一个父节点的值比它的子节点的值都小，那么我们将这样的堆称为小堆；
• 如果一个父节点的值比它的子节点的值都大，那么我们将这样的堆称为大堆；

---

三.堆的实现

我现在随便给出一个数组：

arr[] = { 9,4,6,2,7,1,8,4,8,2 };

该数组可以是一棵二叉树，但是不满足堆的条件，下面我们就来创建一个堆，并将该数组的数据按照堆的规则将它们入堆。（以小堆为例）

---

1.堆的创建

因为是数组型数据结构，所以一开始肯定还是要创建一个堆结构体：

typedef int HPDataType;

typedef struct Heap
{
	HPDataType* data;
	int size;
	int capacity;
}Heap;

紧接着进行初始化：

// 堆的构建
void HeapCreate(Heap* hp)
{
	assert(hp);
	hp->capacity = 0;
	hp->size = 0;
	hp->data = NULL;
}

---

2.堆的销毁

销毁也是同样的操作：

// 堆的销毁
void HeapDestory(Heap* hp)
{
	assert(hp);
	free(hp->data);
	hp->capacity = 0;
	hp->size = 0;
	hp->data = NULL;
}

---

 3.堆顶数据

// 取堆顶的数据
HPDataType HeapTop(Heap* hp)
{
	assert(hp);
	assert(hp->size > 0);
	return hp->data[0];
}

取堆顶数据是要断言堆是否为空。 

---

4.堆的判空

// 堆的判空
bool HeapEmpty(Heap* hp)
{
	assert(hp);
	return hp->size == 0;
}

堆判空比较简单，如果sizeof为0，就说明堆没有数据。 

---

5.堆的数据个数

// 堆的数据个数
int HeapSize(Heap* hp)
{
	assert(hp);
	return hp->size;
}

数据个数即为size。

---

 6.堆的插入

整个入堆的操作分为两部分：

1. 将数据存入堆底；
2. 按照小堆的规则进行调整。

因为数据入堆的时候不一定就是按照小堆的规则，所以我们必须得有一个调整。

那么我们又该如何调整呢？？？

小堆的规则是，父节点的值不大于子节点的值，那如果新入堆的子节点的值要比父节点小，就将它们两个的值进行交换。交换之后，新的父节点还要和它的父节点再进行比较，如果小，那么就还要继续进行交换，就这样一步一步的向上调整。

首先小伙伴们要知道，堆中的节点的序号和数组一样，根节点为0，依次往下排序。

然后是一个很重要的小技巧，那就是，假设一个父节点的序号为N，它的其中一个子节点的序号为n，那么N = （n - 1）/ 2。

通过这一点，我们就可以很容易的实现调整啦。

先来看数据入堆：

//堆的插入
void HeapPush(Heap* hp, HPDataType x)
{
	assert(hp);
	if (hp->size == hp->capacity)
	{
		int newcapacity = hp->capacity == 0 ? 4 : hp->capacity * 2;
		HPDataType* tmp = (HPDataType*)realloc(hp->data,sizeof(HPDataType)*newcapacity);
		if (tmp == NULL)
		{
			perror("HeapPush->malloc");
			exit(-1);
		}
		hp->data = tmp;
		hp->capacity = newcapacity;
	}
	hp->data[hp->size] = x;
	hp->size++;
	AdjustUp(hp->data, hp->size - 1);
}

入堆之后，开始进行调整，我们另建一个向上调整函数，并传入数组的地址和子节点的序号。

//交换
void Swap(HPDataType* x, HPDataType* y)
{
	HPDataType tmp = *x;
	*x = *y;
	*y = tmp;
}
//堆向上调整
void AdjustUp(HPDataType* a, int child)
{
	while (child > 0)
	{
		int parent = (child - 1) / 2;
		if (a[child] < a[parent])
		{
			Swap(&a[child], &a[parent]);
		}
		else
		{
			break;
		}
        child = parent;
		parent = (parent - 1) / 2;
	}
}

因为需要进行交换，所以我们干脆就在写一个交换函数，这样更加方便。

在该函数中，我们首先要记录父节点的序号，然后通过while循换来实现一步一步的向上调整，值得注意的是while循环的条件：child > 0，因为很有可以一直向上调整，直到该子节点成为最上边的根节点，如此一来，它的序号就是0。所以只要它还大于0 ，那么就反复执行循环。

随后进行比较判断，如果子节点要小于父节点，就进行交换，然后让两个child和parent分别向上继承序号。

反之，就不用交换，更不用再执行循环，所以就直接用break打破循环。

如此一来我们就实现了堆的插入。

---

7.堆的删除

有小伙伴会说，堆的删除简单啊，直接size--。但是我要告诉你的是，谁说过堆的删除就是删除最后一个节点了？？？如果是这样，那岂不是太简单了。

所以实际上说堆的删除，都是删除它的根节点。

这就很难办啊，根节点该怎么删除啊？？？

这时候又有小伙伴说，直接让数据都向前覆盖呗，话是这样说，但是假如说，我们一个小堆是1,3,2,4,5，把根节点1删除，剩下的序列是3,2,4,5，3成为新的根节点，但是它的子节点2比它小，这样就不满足小堆的规则了，堆的数据就全乱套了。

那么堆到底该如何进行根节点的删除呢？？？

既要满足把根节点删除，又要满足不破坏堆的结构和规则，为此诞生出了，先将根节点的值和最后一个节点的值交换，再让新根节点进行向下比较调整的方法。

//堆的删除
void HeapPop(Heap* hp)
{
	assert(hp);
	assert(hp->size > 0);
	Swap(&hp->data[0], &hp->data[hp->size - 1]);
	hp->size--;
	AdjustDown(hp->data, hp->size, 0);
}

首先，要断言堆是否为空。

接着，我们将根节点与最后一个节点进行值的交换，再让size--，这样便满足的将根节点的值进行了删除。

但是新的根节点的值不一定满是小堆的规则，它可能比它的子节点的值更大，所以就要开始进行向下调整啦。

//堆向下调整
void AdjustDown(HPDataType* a, int size, int parent)
{
	int child = parent * 2 + 1;
	while (child < size)
	{
		if (child + 1 < size && a[child + 1] < a[child])
		{
			child++;
		}
		if (a[child] < a[parent])
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

向下调整，我们需要传入数组，数组的大小，以及根节点的序号0。

通过公式N = （n - 1）/ 2的逆向操作，我们可以通过父节点的序号来得到它的左子节点的序号，因为要满足小堆的规则，所以向下调整时，我们要找两个子节点中值更小的一个来进行交换。 

所以我们首先要进行一次比较，如果右节点的值大于左节点，就让child++，这样child就是右节点的序号。

紧接着就开始比较两个父子节点的值的大小，如果父比子大，就交换，并向下继承序号，反之就打破循环，结束调整。

最后我们再来分析while循环的判断条件（child < size），如果一直向下调整，就会出现parent成为了最后一层的节点，那么他就没有子节点可以调整了，也就是它的child的序号已经超出size的范围了，所以循环便不再进行。

此外，还有一种特殊情况：

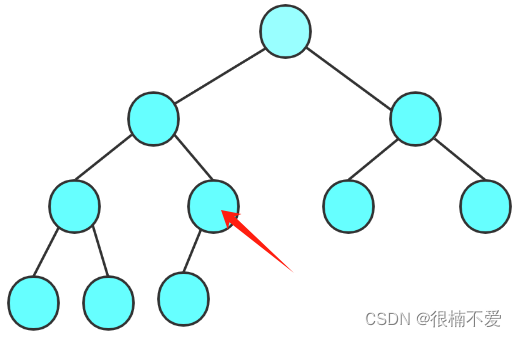
如果此时的父节点为我们的红箭头指向的节点，那么他就只有左子节点，这样我们就不用比较左右节点的大小啦，所以判断左右节点的大小时，需要多加一条child+1 < size，来排除此特殊情况。

---

8.测试

#include "Heap.h"

void test(Heap* hp)
{
	HeapCreate(hp);
	HPDataType arr[] = { 9,4,6,2,7,1,8,4,8,2 };
	int size = sizeof(arr) / sizeof(arr[0]);
	for (int i = 0; i < size; i++)
	{
		HeapPush(hp, arr[i]);
	}
	while (!HeapEmpty(hp))
	{
		printf("%d ", HeapTop(hp));
		HeapPop(hp);
	}
}
int main()
{
	Heap hp;
	test(&hp);
	return 0;
}

因为堆同样不支持直接遍历的操作，所以还是要自己来实现遍历的操作，结果如下：

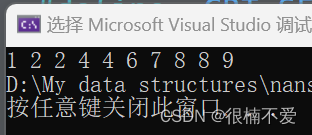
如果想要改为大堆，我们只需要将父子节点的大小比较和兄弟节点的大小比较进行更改即可。

大堆结果如下：

---

四.完整代码展示

1.Heap.h

#include <stdio.h>
#include <stdbool.h>
#include <stdlib.h>
#include <assert.h>

typedef int HPDataType;

typedef struct Heap
{
	HPDataType* data;
	int size;
	int capacity;
}Heap;

// 堆的构建
void HeapCreate(Heap* hp);
// 堆的销毁
void HeapDestory(Heap* hp);
// 堆的插入
void HeapPush(Heap* hp, HPDataType x);
// 堆的删除
void HeapPop(Heap* hp);
// 取堆顶的数据
HPDataType HeapTop(Heap* hp);
// 堆的数据个数
int HeapSize(Heap* hp);
// 堆的判空
bool HeapEmpty(Heap* hp);

---

2.Heap.c

#include "Heap.h"

// 堆的构建
void HeapCreate(Heap* hp)
{
	assert(hp);
	hp->capacity = 0;
	hp->size = 0;
	hp->data = NULL;
}
// 堆的销毁
void HeapDestory(Heap* hp)
{
	assert(hp);
	free(hp->data);
	hp->capacity = 0;
	hp->size = 0;
	hp->data = NULL;
}
//交换
void Swap(HPDataType* x, HPDataType* y)
{
	HPDataType tmp = *x;
	*x = *y;
	*y = tmp;
}
//堆向上调整
void AdjustUp(HPDataType* a, int child)
{
	while (child > 0)
	{
		int parent = (child - 1) / 2;
		if (a[child] > a[parent])
		{
			Swap(&a[child], &a[parent]);
		}
		else
		{
			break;
		}
		parent = (parent - 1) / 2;
		child = (child - 1) / 2;
	}
}
//堆向下调整
void AdjustDown(HPDataType* a, int size, int parent)
{
	int child = parent * 2 + 1;
	while (child < size)
	{
		if (child + 1 < size && a[child + 1] > a[child])
		{
			child++;
		}
		if (a[child] > a[parent])
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}
//堆的插入
void HeapPush(Heap* hp, HPDataType x)
{
	assert(hp);
	if (hp->size == hp->capacity)
	{
		int newcapacity = hp->capacity == 0 ? 4 : hp->capacity * 2;
		HPDataType* tmp = (HPDataType*)realloc(hp->data,sizeof(HPDataType)*newcapacity);
		if (tmp == NULL)
		{
			perror("HeapPush->malloc");
			exit(-1);
		}
		hp->data = tmp;
		hp->capacity = newcapacity;
	}
	hp->data[hp->size] = x;
	hp->size++;
	AdjustUp(hp->data, hp->size - 1);
}
//堆的删除
void HeapPop(Heap* hp)
{
	assert(hp);
	assert(hp->size > 0);
	Swap(&hp->data[0], &hp->data[hp->size - 1]);
	hp->size--;
	AdjustDown(hp->data, hp->size, 0);
}
// 取堆顶的数据
HPDataType HeapTop(Heap* hp)
{
	assert(hp);
	assert(hp->size > 0);
	return hp->data[0];
}
// 堆的数据个数
int HeapSize(Heap* hp)
{
	assert(hp);
	return hp->size;
}
// 堆的判空
bool HeapEmpty(Heap* hp)
{
	assert(hp);
	return hp->size == 0;
}

---

五.总结 

堆最难的点就再于插入和删除，需要考虑父子节点之间的大小关系，但是如果能够理清思绪，问题自然也就迎刃而解啦。