一、前言

       前期我们解释过二叉树的顺序结构（堆）为什么比较适用于完全二叉树，因为如果用数组来实现非完全二叉树，那么数组的中间部分就可能会存在大量的空间浪费。

      而二叉树的链式结构即用链表结构来存储二叉树，这里就没有什么限制了，所有的二叉树都可以用链式结构来存储，因为链式结构存在两个指针分别指向自己的左右孩子，无论是少了左孩子还是少了右孩子，只需要让相应的指针指向NULL就可以了。

       虽然链式结构可以表示所有类型的二叉树，但是由于二叉树本身存储数据的价值并不大（链表、顺序表远远优于二叉树），所以实现增删查改是没有太大意义的，学习链式二叉树真正的意义是学会如何去控制、遍历二叉树的结构，为我们后期学习搜索二叉树做好铺垫。而以下的学习中要重点理解二叉树中的递归思想和分治思想 !

二、链式二叉树的实现

2.1 节点结构体的创建

      创建的方式和单链表的很相似，唯一的区别就是要有两个指针，一个指向自己的左孩子，一个指向自己的右孩子！

typedef int BTDataType;//方便我们后面要存储其他类型的数据的时候方便修改！
typedef struct BinaryTreeNode
{
	BTDataType data;//二叉树节点的数据域
	struct BinaryTreeNode* left;//左孩子
	struct BinaryTreeNode* right;//右孩子
}BTNode;

2.2 二叉树节点的创建

      二叉树节点构建方式和单链表节点的构建方式相同！

BTNode* BuyNode(BTDataType x)
{
	BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));
	if (newnode == NULL)//如果创建不成功
	{
		perror("malloc fail");
		exit(1);
	}
	//如果创建成功
	newnode->data = x;
	newnode->left = newnode->right = NULL;
	return newnode;
}

2.3 前序遍历

为了能够深入前中后续遍历，我们先手动创建一个二叉树，后面都按照这个二叉树来研究

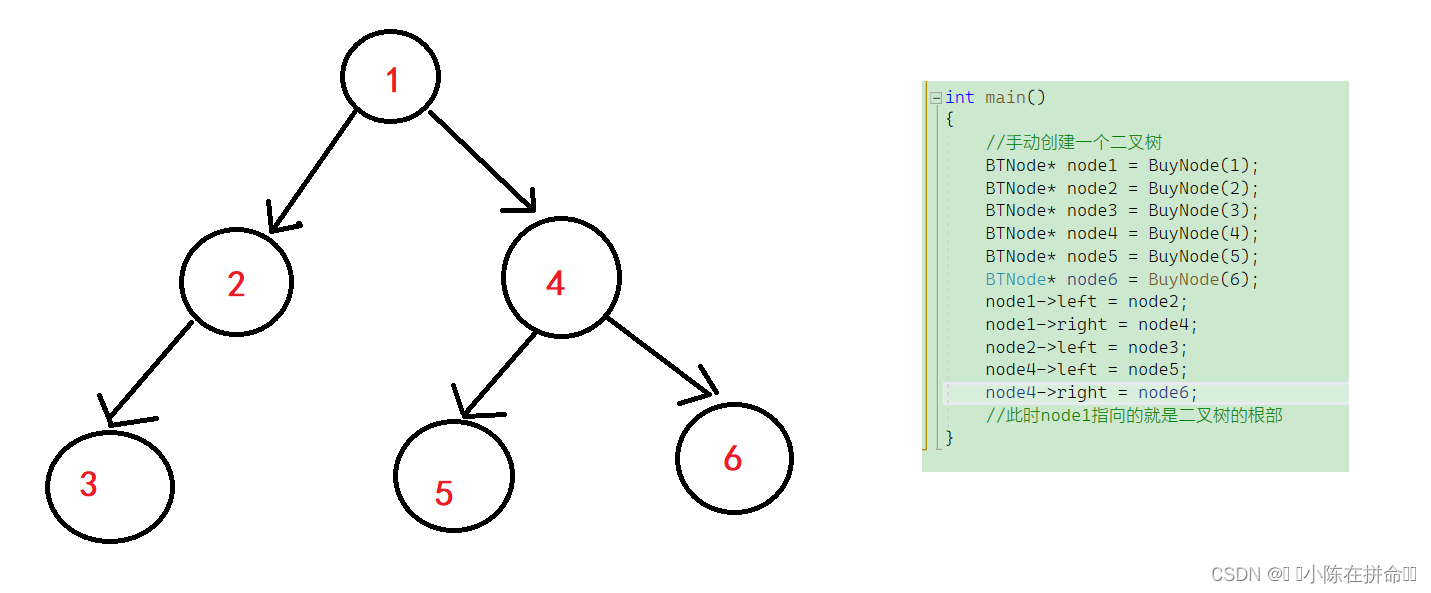
 下面我先给出前中后续的遍历结果，再逐个分析，要注意，没有箭头默认指向空！

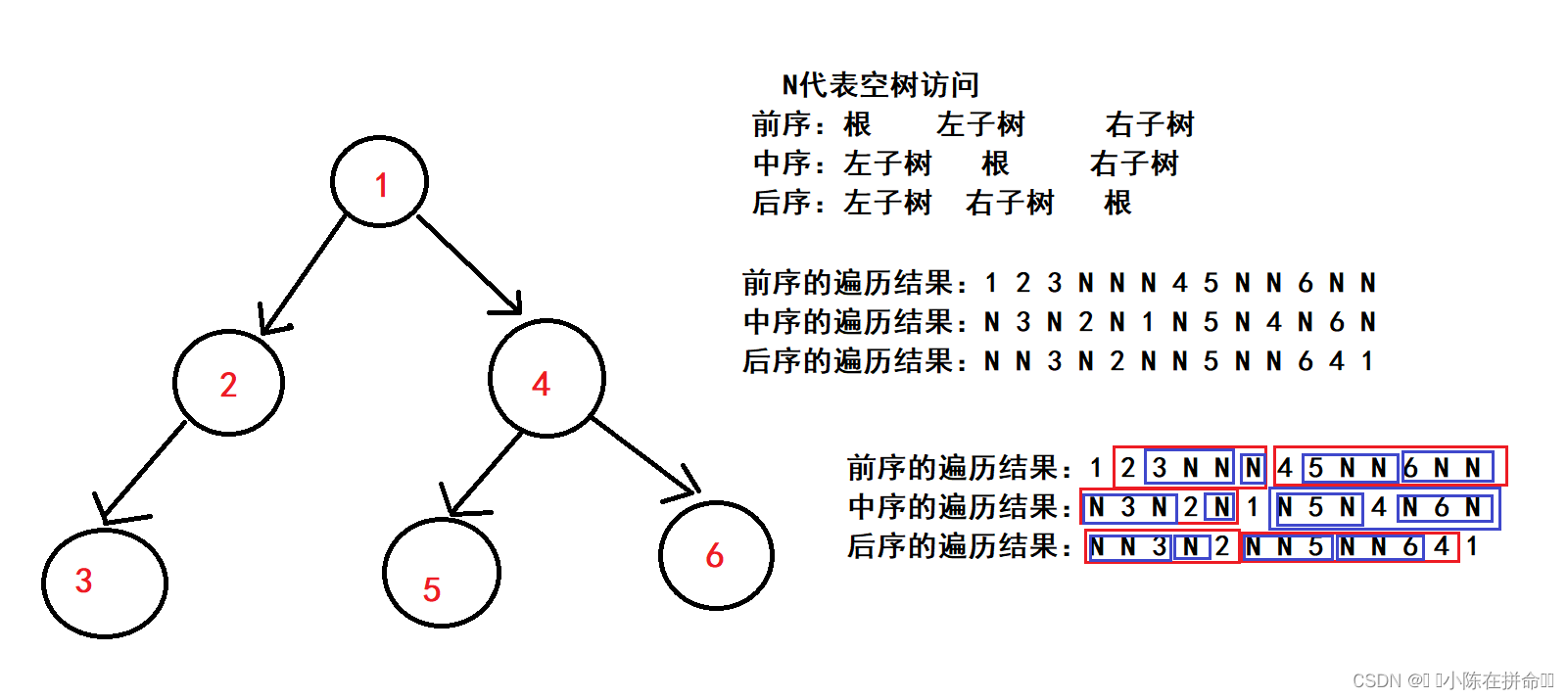
 分析前序：

       前序的顺序是根、左子树、右子树：首先1是根，接着访问1的左子树2,2也是根，再访问2的左子树3，3也是根，再访问3的左子树N，接着访问3的右子树N，，回归到2，对于2来说，他的左子树已经访问完了，然后访问右子树N，回归1，对于1来说，他的左子树已经访问完了，该访问他的右子树4了，4是根，接着访问4的左子树5,5也是根，接着访问5的左子树N，再访问5的右子树N，然后回归5，对于4来说，左子树访问完了，接着访问6,6的左子树是N，然后访问6的右子树N。此时所有节点都访问完了。

      大家可以看看上面的图我画的框框，1这个根右边的2 3 N N N  和4 5 N N 6 N N 分别表示1的左右子树，而对于2这个根来说，3 N N  和  N分别代表2的左右子树，对于4这个根来说，5 N N和6 N N分别代表4的左右子树，对于3、5、6 这三个根来说，他们的左右子树都是N和N。

       那么怎么写前序遍历的代码呢？根据上一段的思路我们可以发现，对于根1来说，他的左子树是以2为根的树，他的右子树是以4为根的树，而对于2来说，他的左子树是以3为根的树，右子树是N，对于4来说，他的左子树是以5为根的树，他的右子树是以6为根的树， 而对于3、5、6来说，他们其实也是根，左右子树都是N。所以将问题转化为递归问题。

void PreOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("N ");
		return;
	}
	printf("%d ", root->data);
	PreOrder(root->left);
	PreOrder(root->right);
}

画一下递归展开图：

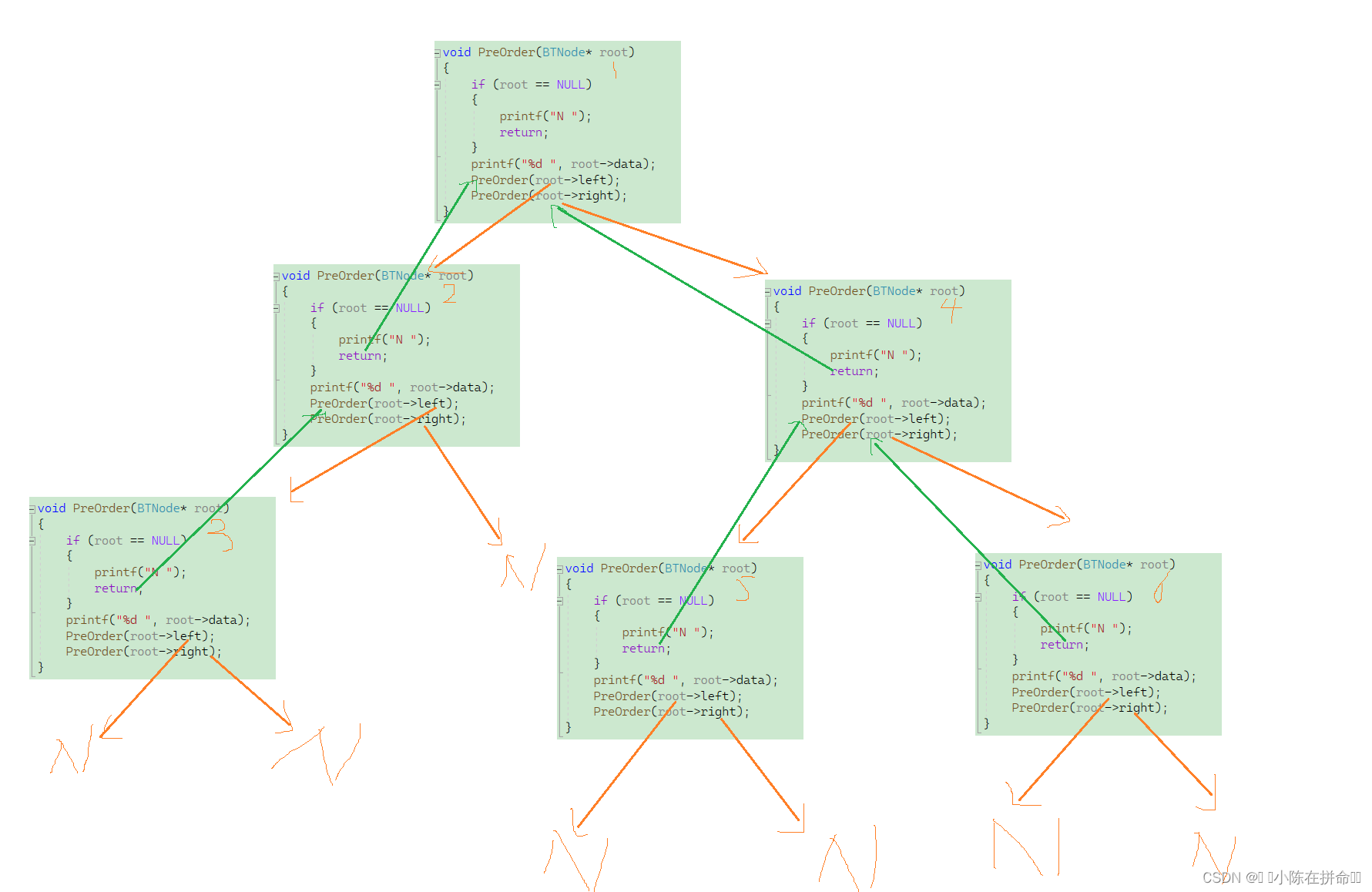
时间复杂度是O（N）  因为每个节点都遍历了一次

空间复杂度是O（h） 通过上图可以看出，当开辟h个的函数栈帧后，后续的空间都是在前一个空间释放后复用的，所以最多同时只有h个栈帧空间被开辟，根据空间可以重复利用的特点，空间复杂度是o（h）!

中序遍历和后序遍历的方法是一样的，后面就不分析了

2.4 中序遍历

void InOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("N ");
		return;
	}
	InOrder(root->left);
	printf("%d ", root->data);
	InOrder(root->right);
}

2.5 后序遍历

void PostOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("N ");
		return;
	}
	PostOrder(root->left);
	PostOrder(root->right);
	printf("%d ", root->data);
}

2.6 层序遍历

       层序遍历是一层一层遍历，之前无论是前序、中序、还是后序遍历，都是根据父子关系（父亲会指向自己的左右孩子）转化成递归问题去遍历的， 但是链式二叉树的指针指向并不指向兄弟节点，所以这边如果要一层一层遍历，需要用到队列。

     选择队列的原因是利用队列队头出队尾进的特点，下面进行分析：

 

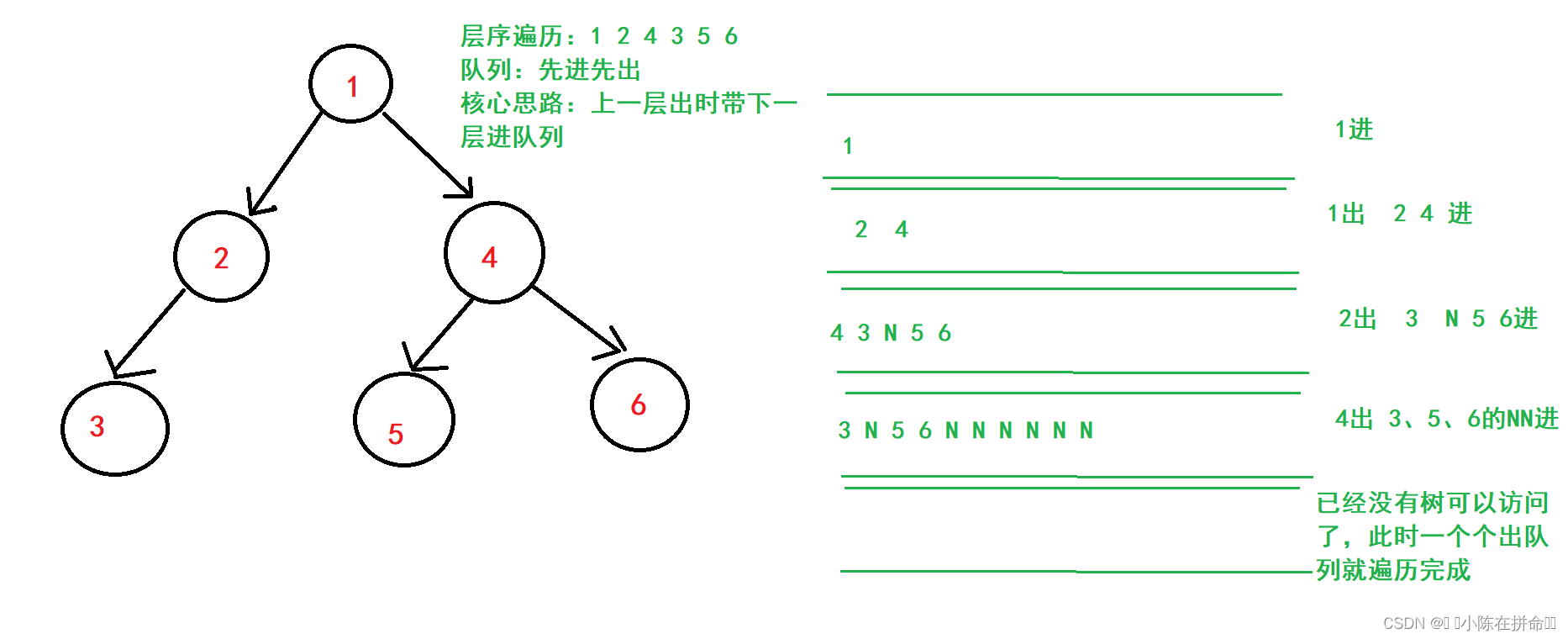
Queue.h

 

void LevelOrder(BTNode* root)
{
	Queue q;
	QueueInit(&q);
	if (root)//如果不为NULL，就进队列
		QueuePush(&q, root);
	while (!QueueEmpty(&q))//队列为空，就是遍历完成
	{
		BTNode* front = QueueFront(&q);//让每一次循环过来的节点变成根部，再去访问左右子树
		QueuePop(&q);//记录完一个元素就出队列
		printf("%d ", front->data);
		if(front->left)
			QueuePush(&q, front->left);//左节点不为空，进队列
		if (front->right)
			QueuePush(&q, front->right);//右节点不为空，进队列
	}
	printf("\n");
	//遍历完了就可以销毁队列了
	QueueDestory(&q);
}

2.7 二叉树节点个数

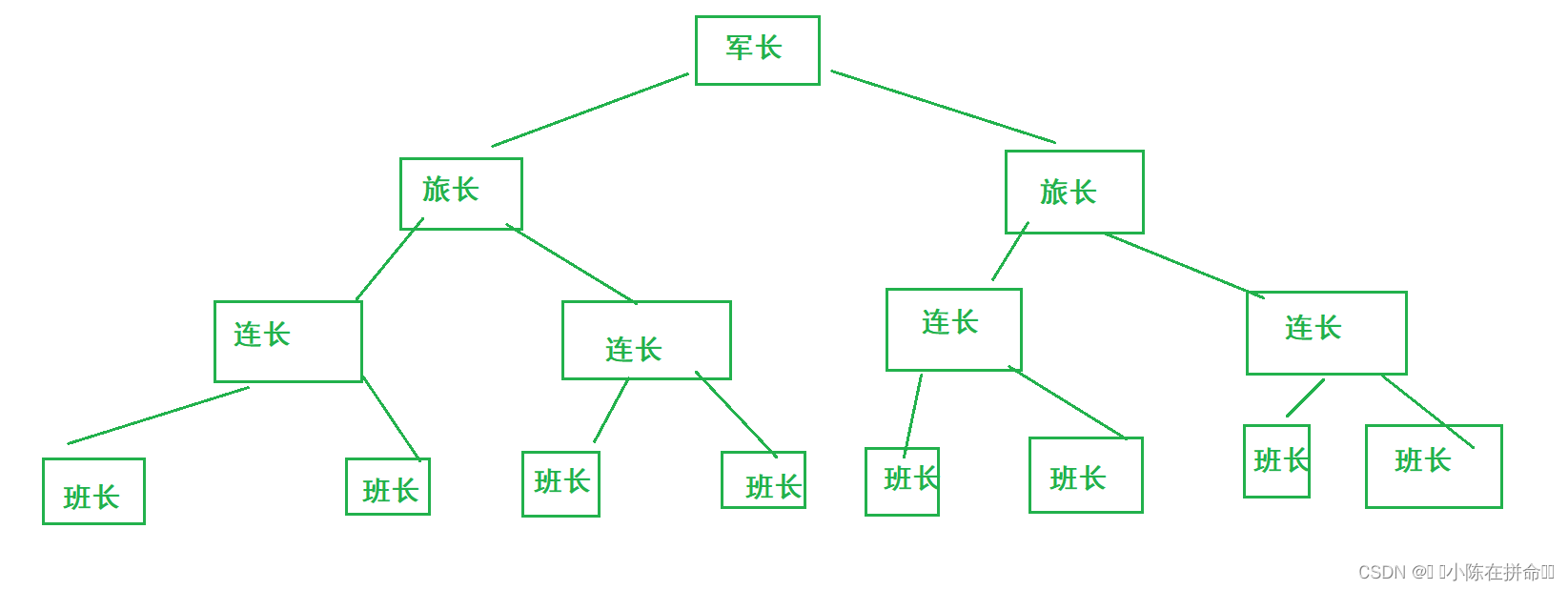
我们先按照按照军棋里的模式来解释分治思想：

       假设军长要统计总人数，有两个方法，一个是军长一级一级去视察数人，这显然是效率比较低的， 而另一个方法就是分而治之——利用自己的职权将任务移交给下级，军长把任务分配给两个旅长，然后旅长统计过来的人数加上自己就是全军人数，旅长又分配给连长，将两个连长统计的人数加上自己就是全旅人数，以此类推……

     

 

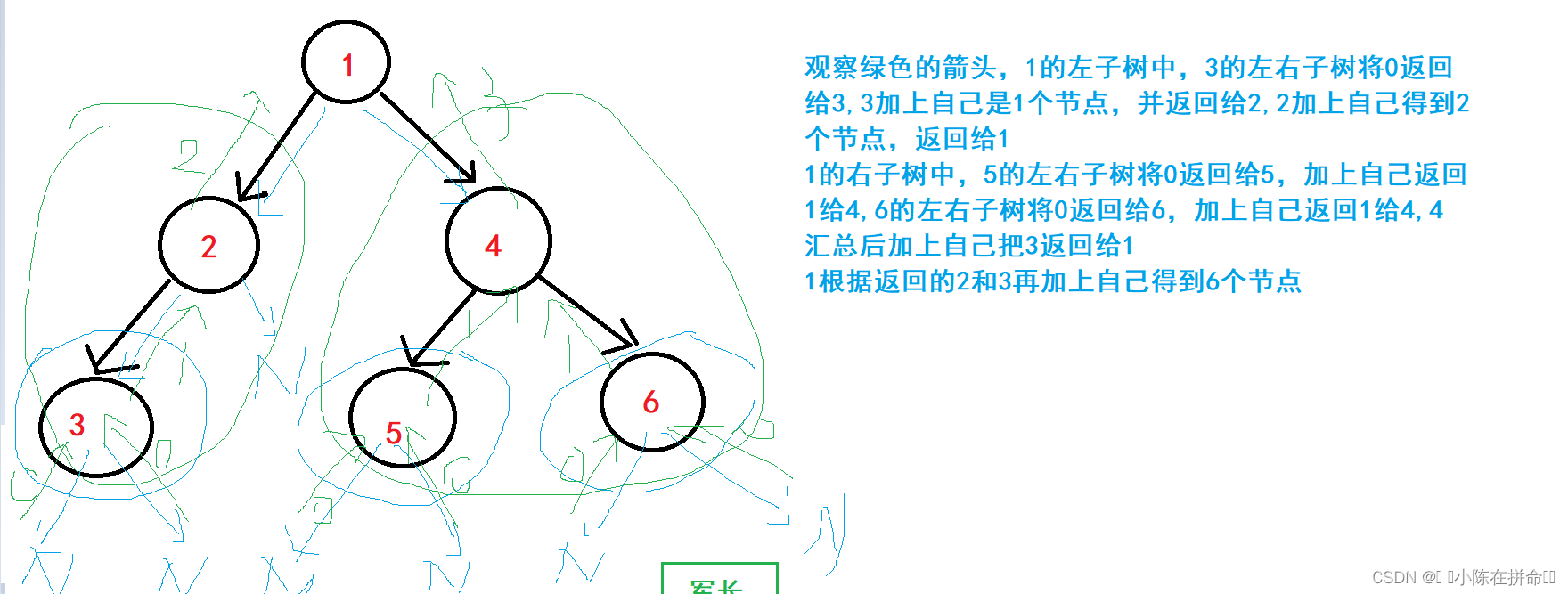
int BinaryTreeSize(BTNode* root)
{
	return root == NULL ? 0 : BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}

2.8 二叉树叶子节点个数

    还是利用分治思想，叶子节点的特征是左右子树都为NULL，我们还是按照分治思想将这个任务拆分下去

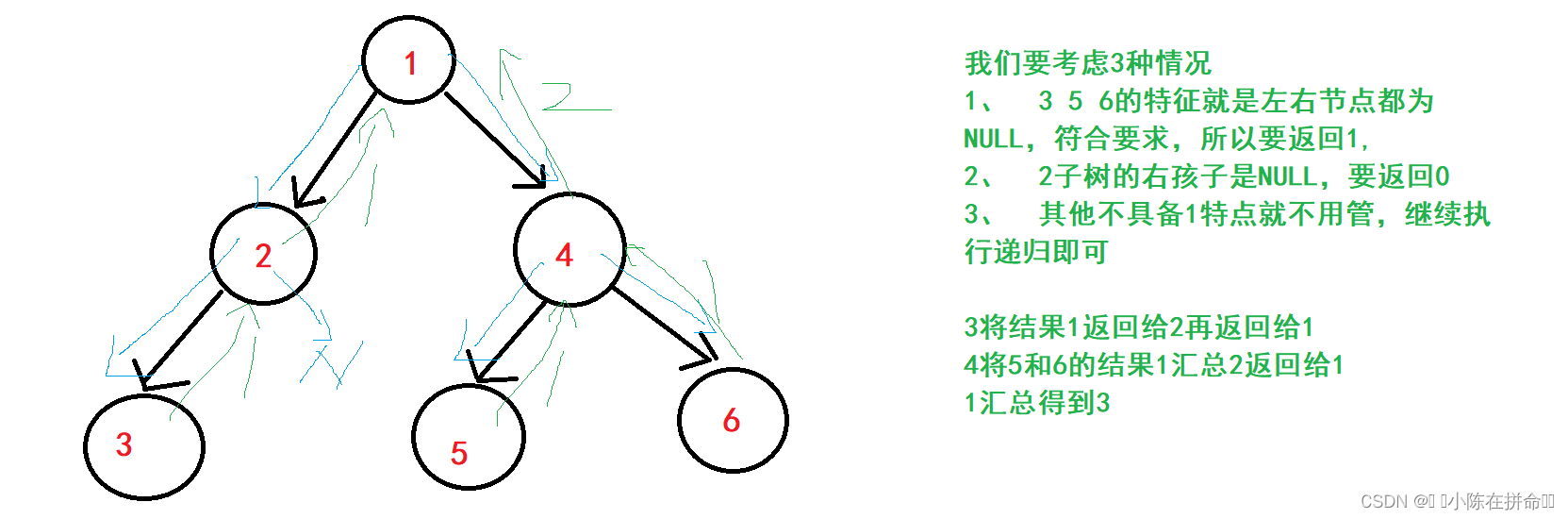
int BinaryTreeLeafSize(BTNode* root)
{
	if (root == NULL)
		return 0;
	if (root->left == NULL && root->right == NULL)
		return 1;
	return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}

2.9 二叉树第k层节点

还是利用分治思想，将求第k层节点转化为求左子树的k-1层节点加上右子树的k-1层节点。

 

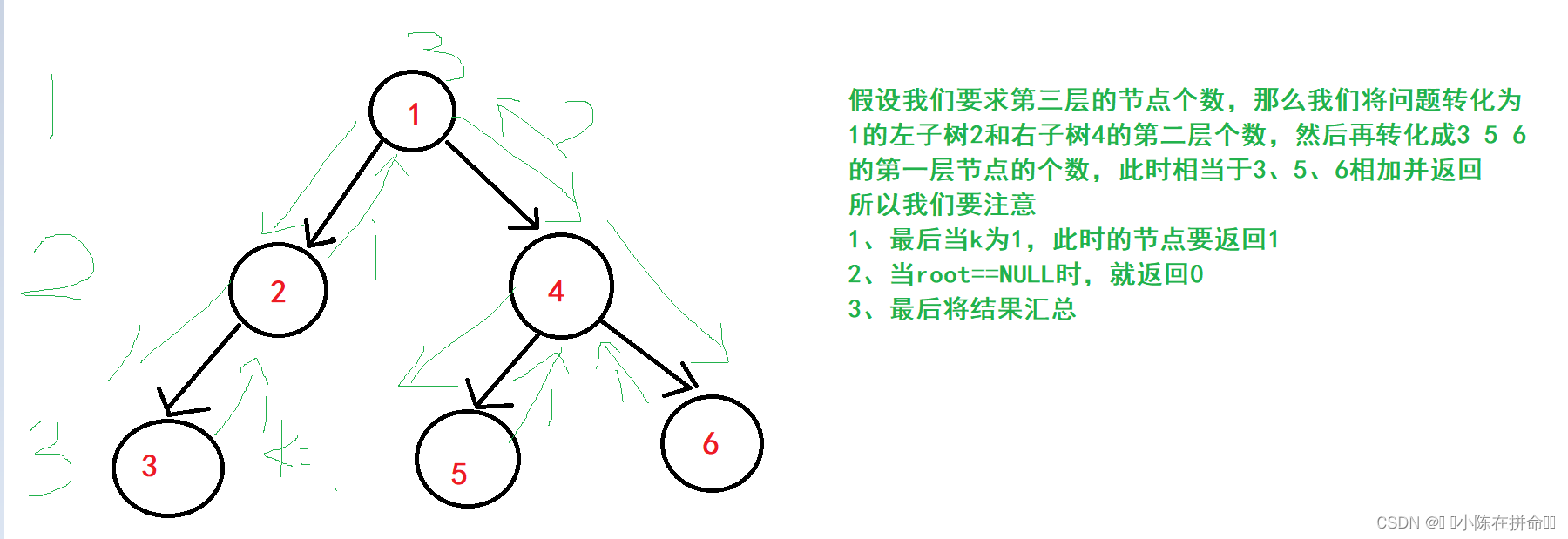
int BinaryTreeLevelKSize(BTNode* root,int k)
{
	if (root == NULL)
		return 0;
	if (k == 1)
		return 1;
	return BinaryTreeLevelKSize(root->left,k-1) + BinaryTreeLevelKSize(root->right,k-1);
}

2.10 二叉树的高度

还是利用分治思想，求高度转化为比较左右子树的大小再+1

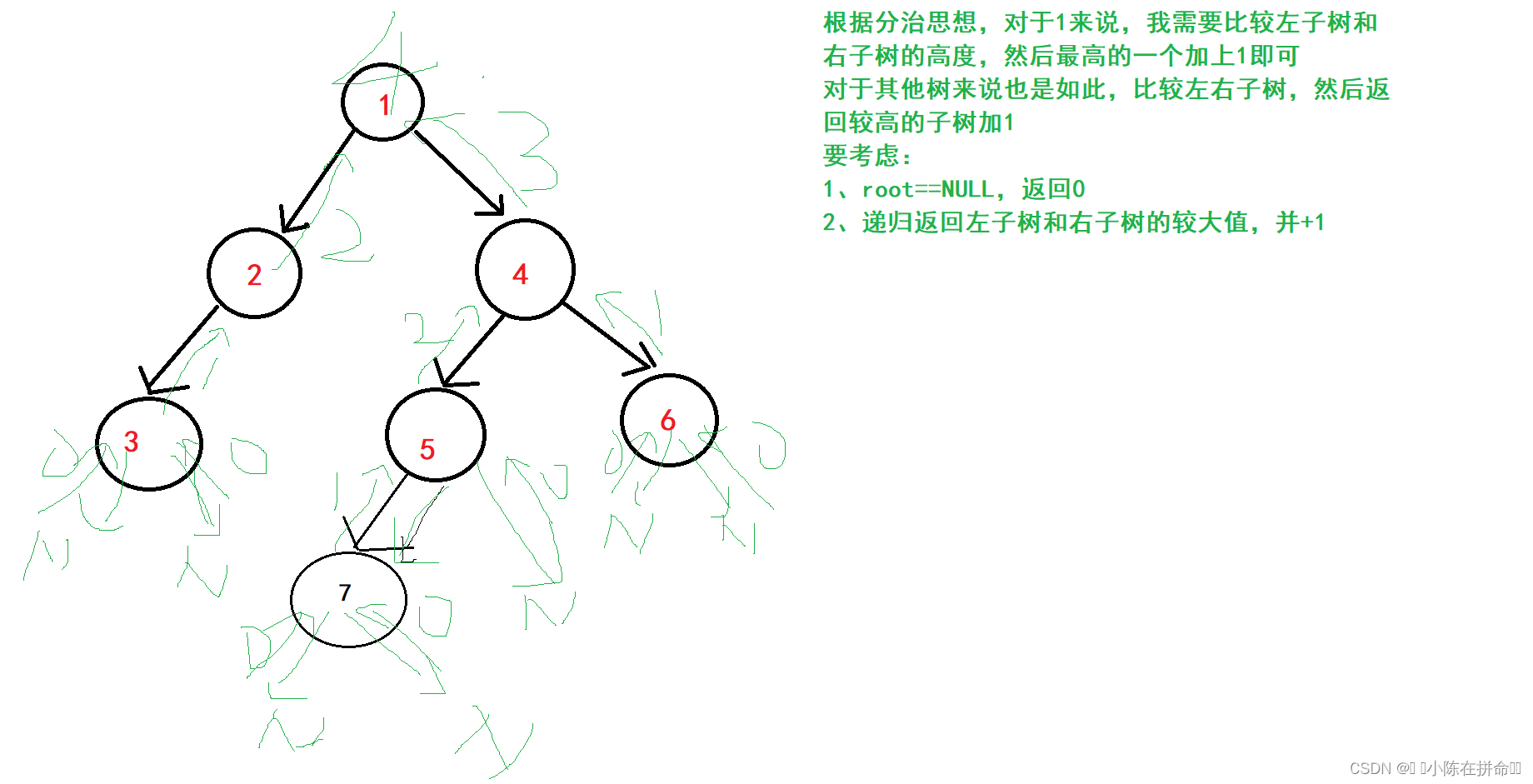
​​int BinaryTreeHeight(BTNode* root)
{
	if (root == NULL)
		return 0;
	return BinaryTreeHeight(root->left) > BinaryTreeHeight(root->right) ? BinaryTreeHeight(root->left) + 1 : BinaryTreeHeight(root->right) + 1;
}

 其实这样写是有问题的！！！因为每次我递归比较完后，并没有记录最大值，所以导致每次递归的时候最大值都得再重新递归一次！！如果树节点高度特别高的话，就很可能会出现这样的问题。

改进版：

int BinaryTreeHeight(BTNode* root)
{
	if (root == NULL)
		return 0;
	int LeftHeight = BinaryTreeHeight(root->left);
	int RightHeight = BinaryTreeHeight(root->right);
	return LeftHeight > RightHeight ? LeftHeight + 1 : RightHeight + 1;
}

 所以我们在递归时使用三目表达式要注意：如果比较的过程已经递归一次了，比较的结果就不要再去递归了！！可以及时的记录值！！

2.11 二叉树查找值为x的节点

还是利用分治思想,转化为在左子树和右子树中找

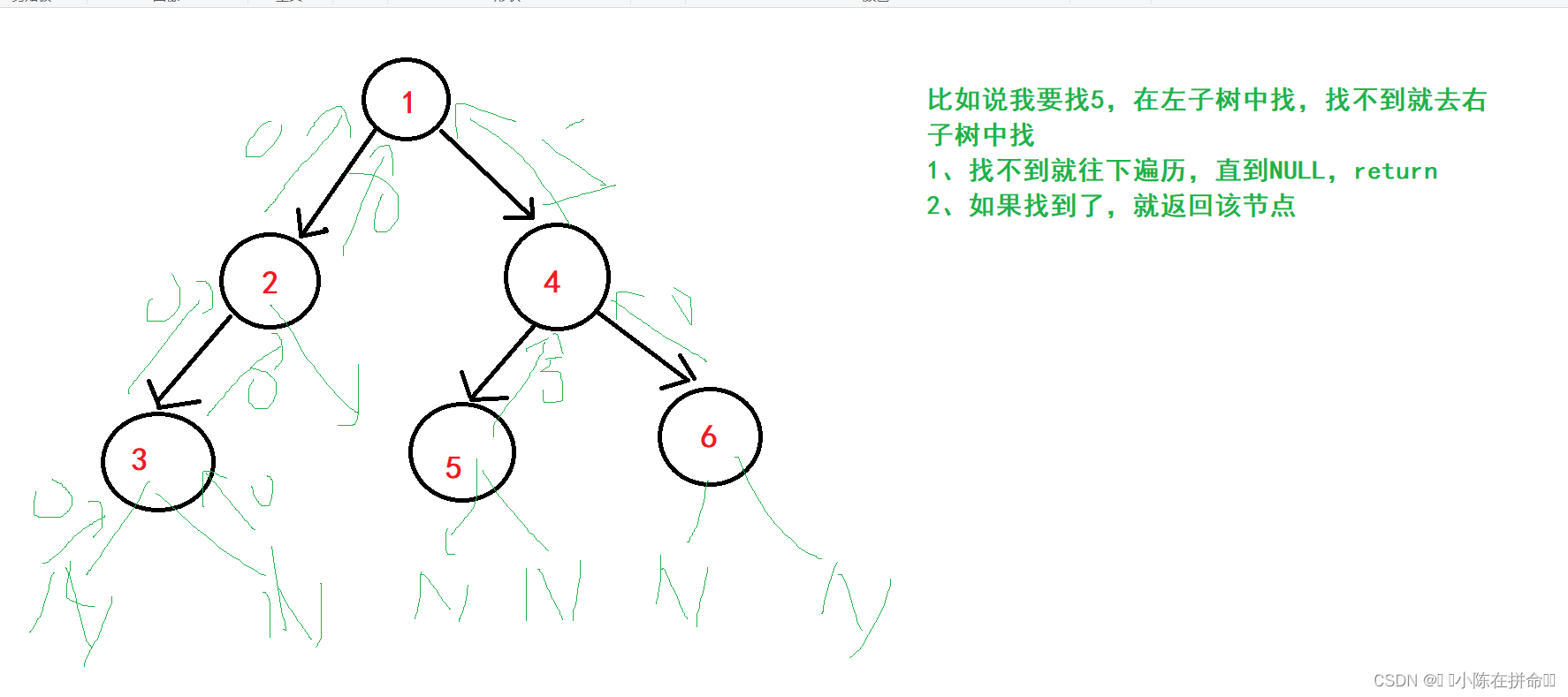
BTNode* BTFind(BTNode* root, BTDataType x)
{
	if (root == NULL)
		return NULL;
	if (root->data == x)
		return root;
	BTNode* ret1 = BTFind(root->left, x);
	if (ret1)
		return ret1;
	BTNode* ret2 = BTFind(root->right, x);
	if (ret2)
		return ret2;
	return NULL;
}

2.12 通过前序遍历数组构建二叉树

     之前我们构建二叉树是一个节点一个节点去手动连接，这次我们尝试自己利用前序遍历数组去构建二叉树，比如abc##de#g##f###

 

BTNode* BTCreate(char*arr,int*pi)
{
	if (arr[*pi] == '#')
	{
		(*pi)++;
		return NULL;
	}
	BTNode* root = BuyNode(arr[*pi]);
	(*pi)++;
	root->left = BTCreate(arr, pi);
	root->right = BTCreate(arr, pi);
	return root;
}

 递归展开图：

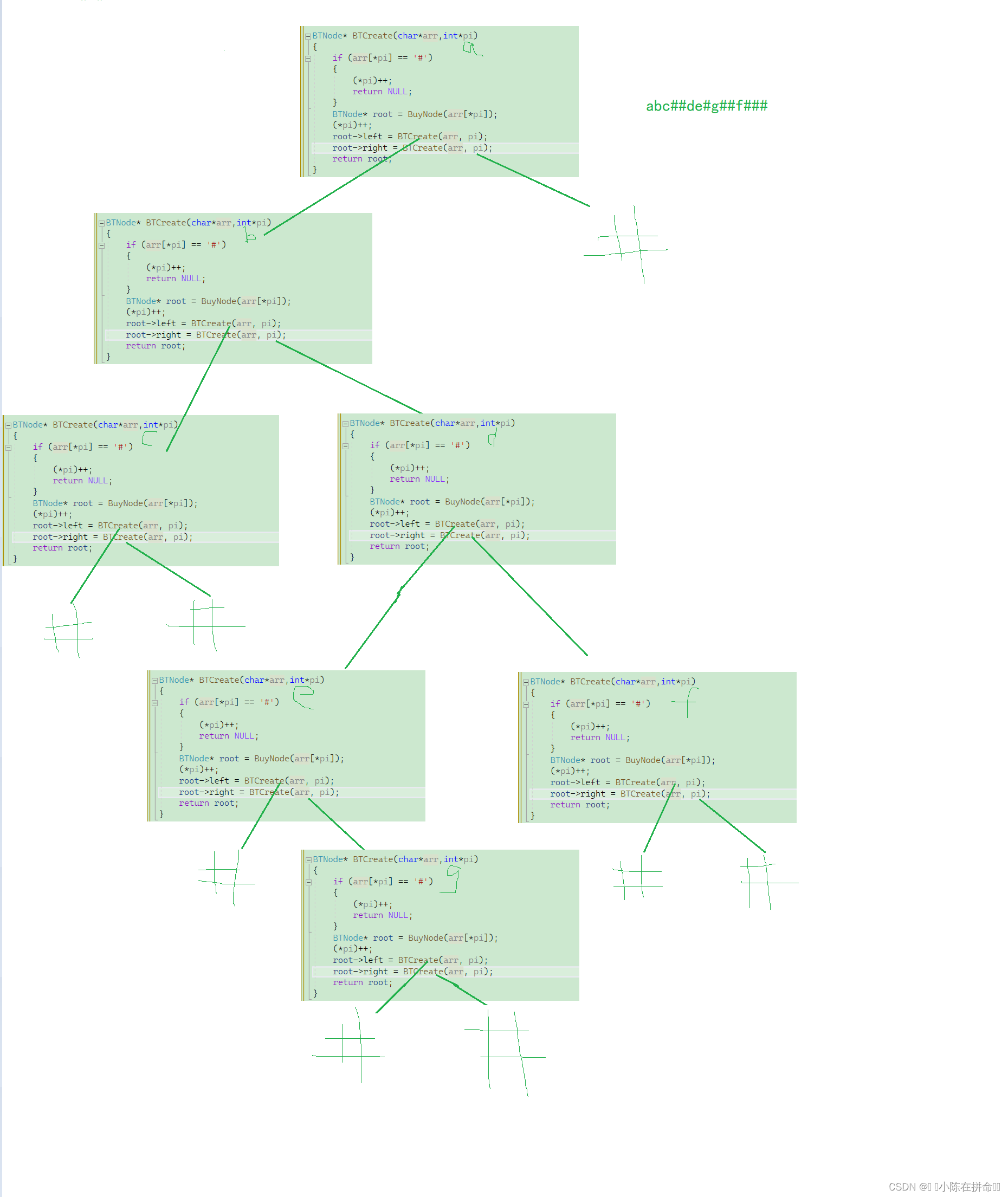
2.13 二叉树销毁

       二叉树要销毁，就要遍历每个节点，因为我们如果先销毁根，那么就很可能找不到他的左子树和右子树了，除非销毁根之前记录一下，但是这样比较麻烦，所以我们选择后序遍历，先销毁左子树，再销毁右子树，再销毁根。

void BTDestory(BTNode* root)
{
	if (root == NULL)
		return;
	BTDestory(root->left);
	BTDestory(root->right);
	free(root);
	//root = NULL;没用
}

注意：这里的参数是一级指针，而root本身也是指针，所以在这里对root置NULL，是没有意义的，所以要使用的话，要在main函数中手动置空（这里不用二级指针的原因是为了保持接口一致性）！！

2.14 判断二叉树是否是完全二叉树

         完全二叉树的特点就是：前h-1层是满的，最后一层从前往后要到最后才会访问到NULL，所以们可以分析一下他的特点：

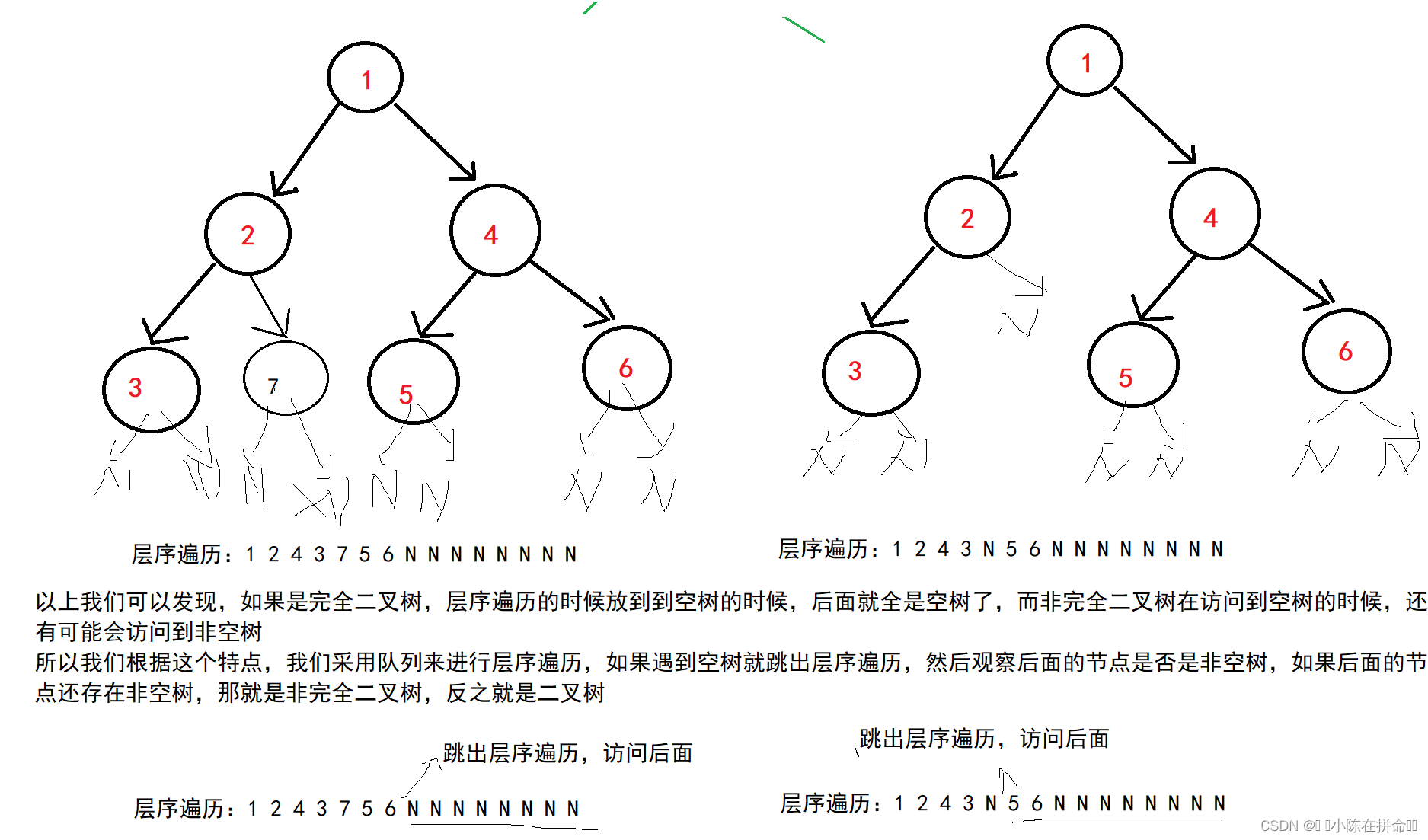
bool BTComplete(BTNode* root)
{
	Queue q;
	QueueInit(&q);
	if (root)
		QueuePush(&q, root);
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);//记录该结果，然后再pop出去
		QueuePop(&q);

		if (front == NULL)
			break;
		QueuePush(&q, root->left);
		QueuePush(&q, root->right);
	}
	//跳出循环后，检查后面的节点是不是还有非空节点，有的话就是非完全二叉树
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);//记录该结果，然后再pop出去
		QueuePop(&q);
		if (front)
		{
			QueueDestory(&q);//队列一定别忘了销毁
			return false;
		}
		QueueDestory(&q);
		return true;
	}
}

 

2.15 判断两颗二叉树是否完全相同

我们还是用分治思想，前序遍历比较

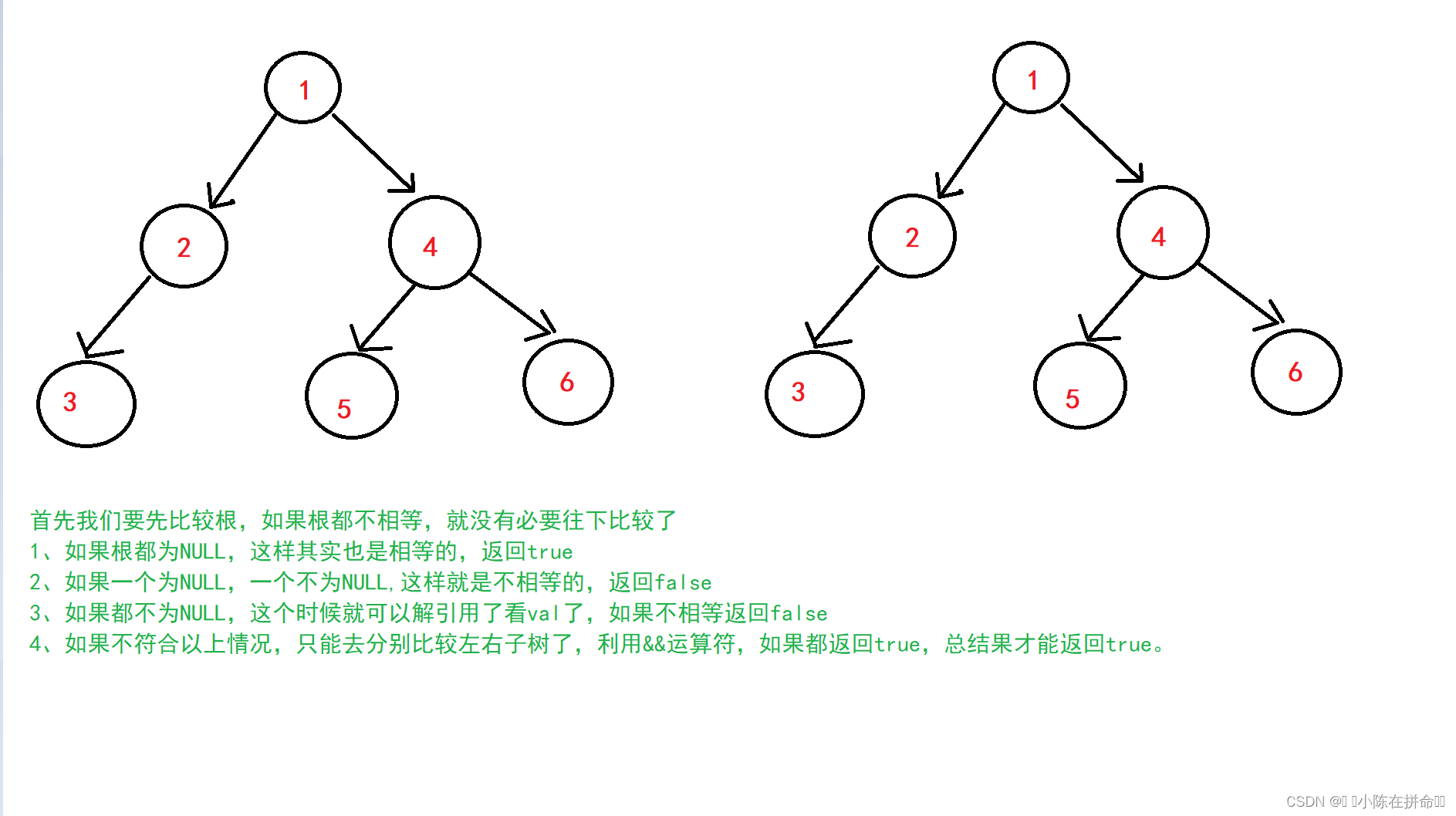
bool IsBTSame(BTNode* root1, BTNode* root2)
{
	if (root1 == NULL && root2 == NULL)
		return true;
	if (root1 == NULL || root2 == NULL)
		return false;
	//此时节点肯定不为NULL了，可以解引用找到val
	if (root1->data != root2->data)
		return false;
	//不相等的话只能去找自己的左右子树，左右子树都返回true最后结果才能返回true
	return IsBTSame(root1->left, root2->left) && IsBTSame(root1->right, root2->right);
}

三、链式二叉树实现的全部代码

前两个文件只是因为层序遍历和判断完全二叉树会用到，重点还是看后面两个文件

3.1 queue.h

#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
#include<assert.h>
struct BinaryTreeNode;//为了防止嵌套调用，这里声明一下
typedef struct BinaryTreeNode* QDatatype;//方便后面修改存储数据的数据类型
typedef struct QueueNode//队列结点的数据结构
{
	QDatatype data;//存储数据
	struct QueueNode* next;
}QNode;

typedef struct Queue
{
	QNode* phead;//指向队头，用于出队（头删）
	QNode* ptail;//指向队尾，用于入队（尾插）
	int size;//记录有效元素个数
}Queue;//创建一个队列相关结构体
void QueueInit(Queue* pq);//队列的初始化
void QueuePush(Queue* pq, QDatatype x);//队列的入队（尾插）
void QueuePop(Queue* pq);//队列的出队(头删)
QDatatype QueueFront(Queue* pq);//获取队列头部元素
QDatatype QueueBack(Queue* pq);//获取队列尾部元素
int QueueSize(Queue* pq);//获取队列中有效元素个数
bool QueueEmpty(Queue* pq);//判断队列是否为空
void QueueDestory(Queue* pq);//队列的销毁

3.2 queue.c

#include"Queue.h"
void QueueInit(Queue* pq)
{
	assert(pq);//判断传的是不是空指针
	pq->phead = pq->ptail = NULL;
	pq->size = 0;//因为队列不像栈一样，有一个top表示栈顶元素的下标
	//所以如果我们想知道这个队列的有效数据个数，就必须遍历队列
	//由于其先进先出的特性，我们默认只能访问到头元素和尾元素
	//所以必须访问一个头元素，就出队列一次，这样才能实现遍历
	//但是这样的代价太大了，为了方便，我们直接用size
}

void QueuePush(Queue* pq, QDatatype x)
{
	assert(pq);
    //入队必须从队尾入！
	QNode* newnode = (QNode*)malloc(sizeof(QNode));//创建一个新节点
	if (newnode==NULL)//如果新节点申请失败，退出程序
	{
		perror("malloc fail");
	}
	//新节点创建成功，给新节点初始化一下
	newnode->data = x;
	newnode->next = NULL;
	//开始入队
	//如果直接尾插的话，由于会用到ptail->next,所以得考虑队列为空的情况
	if (pq->ptail== NULL)//如果为空，直接把让新节点成为phead和ptail
	{
		//按道理来说，如果ptail为空，phead也应该为空
		// 但是有可能会因为我们的误操作使得phead不为空，这个时候一般是我们写错的问题
		//所以使用assert来判断一下，有问题的话会及时返回错误信息
		assert(pq->phead == NULL);
		pq->phead = pq->ptail = newnode;
	}
	else
	{
		pq->ptail->next = newnode;
		pq->ptail = newnode;
	}
	pq->size++;
}

void QueuePop(Queue* pq)
{
	assert(pq);
	//如果队列为空，没有删除的必要
	assert(!QueueEmpty(pq));
	//队列中的出队列相当于链表的头删
	//如果直接头删，那么如果队列只有一个有效数据的话，那么我们将phead的空间释放掉，但是没有将ptail给置空
	//这样会导致ptail成为一个野指针，所以我们需要考虑只有一个节点多个节点的情况
	if (pq->phead->next == NULL)//一个节点的情况,直接将这个节点释放并置空即可
	{
		free(pq->phead);
		pq->phead = pq->ptail = NULL;//置空，防止野指针
	}
	else//多个节点的情况，直接头删

	{
		QNode* next = pq->phead->next;//临时指针记住下一个节点
		free(pq->phead);
		pq->phead = next;//让下一个节点成为新的头
	}
	pq->size--;
}

QDatatype QueueFront(Queue* pq)
{
	assert(pq);
	assert(!QueueEmpty(pq));//队列如果为空，则不可能找得到队列头元素
	//队列不为空的时候，直接返回phead指向的数据
	return pq->phead->data;
}

QDatatype QueueBack(Queue* pq)
{
	assert(pq);
	assert(!QueueEmpty(pq));//队列如果为空，则不可能找得到队尾元素
	//队列不为空的时候，直接返回ptail指向的数据
	return pq->ptail->data;
}

int QueueSize(Queue* pq)
{
	assert(pq);
	return pq->size;
}

bool QueueEmpty(Queue* pq)//链表为空的情况，可以根据容量，也可以根据ptail==NULL&&phead==NULL
{
	assert(pq);
	return pq->ptail == NULL && pq->phead == NULL;
}

void QueueDestory(Queue* pq)
{
	assert(pq);//判断传的是不是空指针
	//要逐个节点释放
	QNode* pcur = pq->phead;
	while (pcur)
	{
		QNode* next = pcur->next;
		free(pcur);
		pcur = next;
	}
	pq->phead = pq->ptail = NULL;
	pq->size = 0;
}

3.3 BT.h

#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>
#include"Queue.h"
typedef int BTDataType;//方便我们后面要存储其他类型的数据的时候方便修改！
typedef struct BinaryTreeNode
{
	BTDataType data;
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
}BTNode;

BTNode* BuyNode(BTDataType x);
void PreOrder(BTNode* root);//前序遍历
void InOrder(BTNode* root);//中序遍历
void PostOrder(BTNode* root);//后序遍历
void LevelOrder(BTNode* root);//层序遍历
int BTSize(BTNode* root);//二叉树节点个数
int BTLeafSize(BTNode* root);//二叉树的叶子节点个数
int BTLevelKSize(BTNode* root, int k);//二叉树第k层的节点个数
int BTHeight(BTNode* root);//二叉树的高度
BTNode* BTFind(BTNode* root, BTDataType x);//二叉树找值为x的点
BTNode* BTCreate(char* arr,int*pi);//根据前序数组创建二叉树
void BTDestory(BTNode* root);//销毁二叉树
bool BTComplete(BTNode* root);//判断是否完全二叉树
bool IsBTSame(BTNode* root1, BTNode* root2);//判断两个二叉树是否完全相等

3.4 BT.c

#include"BTtree.h"

BTNode* BuyNode(BTDataType x)
{
	BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));
	if (newnode == NULL)//如果创建不成功
	{
		perror("malloc fail");
		exit(1);
	}
	//如果创建成功
	newnode->data = x;
	newnode->left = newnode->right = NULL;
	return newnode;
}

void PreOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("N ");
		return;
	}
	printf("%d ", root->data);
	PreOrder(root->left);
	PreOrder(root->right);
}

void InOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("N ");
		return;
	}
	InOrder(root->left);
	printf("%d ", root->data);
	InOrder(root->right);
}

void PostOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("N ");
		return;
	}
	PostOrder(root->left);
	PostOrder(root->right);
	printf("%d ", root->data);
}

void LevelOrder(BTNode* root)
{
	Queue q;
	QueueInit(&q);
	if (root)//如果不为NULL，就进队列
		QueuePush(&q, root);
	while (!QueueEmpty(&q))//队列为空，就是遍历完成
	{
		BTNode* front = QueueFront(&q);//让每一次循环过来的节点变成根部，再去访问左右子树
		QueuePop(&q);//记录完一个元素就出队列
		printf("%d ", front->data);
		if(front->left)
			QueuePush(&q, front->left);//左节点不为空，进队列
		if (front->right)
			QueuePush(&q, front->right);//右节点不为空，进队列
	}
	printf("\n");
	//遍历完了就可以销毁队列了
	QueueDestory(&q);
}

int BTSize(BTNode* root)
{
	return root == NULL ? 0 : BTSize(root->left) + BTSize(root->right) + 1;
}

int BTLeafSize(BTNode* root)
{
	if (root == NULL)
		return 0;
	if (root->left == NULL && root->right == NULL)
		return 1;
	return BTLeafSize(root->left) + BTLeafSize(root->right);
}

int BTLevelKSize(BTNode* root,int k)
{
	if (root == NULL)
		return 0;
	if (k == 1)
		return 1;
	return BTLevelKSize(root->left,k-1) + BTLevelKSize(root->right,k-1);
}

int BTHeight(BTNode* root)
{
	if (root == NULL)
		return 0;
	int LeftHeight = BTHeight(root->left);
	int RightHeight = BTHeight(root->right);
	return LeftHeight > RightHeight ? LeftHeight + 1 : RightHeight + 1;
}

BTNode* BTFind(BTNode* root, BTDataType x)
{
	if (root == NULL)
		return NULL;
	if (root->data == x)
		return root;
	BTNode* ret1 = BTFind(root->left, x);
	if (ret1)
		return ret1;
	BTNode* ret2 = BTFind(root->right, x);
	if (ret2)
		return ret2;
	return NULL;
}

BTNode* BTCreate(char*arr,int*pi)
{
	if (arr[*pi] == '#')
	{
		(*pi)++;
		return NULL;
	}
	BTNode* root = BuyNode(arr[*pi]);
	(*pi)++;
	root->left = BTCreate(arr, pi);
	root->right = BTCreate(arr, pi);
	return root;
}

void BTDestory(BTNode* root)
{
	if (root == NULL)
		return;
	BTDestory(root->left);
	BTDestory(root->right);
	free(root);
	//root = NULL;没用
}

bool BTComplete(BTNode* root)
{
	Queue q;
	QueueInit(&q);
	if (root)
		QueuePush(&q, root);
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);//记录该结果，然后再pop出去
		QueuePop(&q);

		if (front == NULL)
			break;
		QueuePush(&q, root->left);
		QueuePush(&q, root->right);
	}
	//跳出循环后，检查后面的节点是不是还有非空节点，有的话就是非完全二叉树
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);//记录该结果，然后再pop出去
		QueuePop(&q);
		if (front)
		{
			QueueDestory(&q);//队列一定别忘了销毁
			return false;
		}
		QueueDestory(&q);
		return true;
	}
}

bool IsBTSame(BTNode* root1, BTNode* root2)
{
	if (root1 == NULL && root2 == NULL)
		return true;
	if (root1 == NULL || root2 == NULL)
		return false;
	//此时节点肯定不为NULL了，可以解引用找到val
	if (root1->data != root2->data)
		return false;
	//不相等的话只能去找自己的左右子树，左右子树都返回true最后结果才能返回true
	return IsBTSame(root1->left, root2->left) && IsBTSame(root1->right, root2->right);
}