斐波那契数列用于一维探索的单峰函数之中，用于求解最优值的方法。其主要优势为，在第一次迭代的时候求解两个函数值，之后每次迭代只需求解一次 。

一、第N个泰波那契数

. - 力扣（LeetCode）第N个泰波那契数

class Solution {
public:
    int tribonacci(int n) 
    {
       //边界情况
       if(n==0||n==1) return n;
       if(n==2)  return 1;
       //建表
       vector<int> dp(n+1);
       dp[1]=dp[2]=1;
       //开始填表
       for(int i=3;i<=n;++i)  dp[i]=dp[i-1]+dp[i-2]+dp[i-3];
       return dp[n];
    }
};

时间复杂度O（N）,空间复杂度为O（N）

是否还有可以优化的方法呢？？那就是该题可以使用滚动数组！ 

class Solution {
public:
    int tribonacci(int n) 
    {
       //边界情况
       if(n==0||n==1) return n;
       if(n==2)  return 1;
       //滚动数组
      int a=0,b=1,c=1,d=0;
       //开始滚动
       for(int i=3;i<=n;++i)  
       {
        d=a+b+c;
        a=b;b=c;c=d;
       }
       return d;
    }
};

时间复杂度O（N）,空间复杂度为O（1） 

二、三步问题

. - 力扣（LeetCode）三步问题

思路1：dp[i]表示从起点到达i位置一共有几种方法

class Solution {
public:
    int waysToStep(int n) 
    {
        const int MOD=1e9+7;
       //边界情况
       if(n==1||n==2) return n;
       if(n==3) return 4;
       //建立dp表
       vector<int> dp(n+1);
       //初始化
       dp[1]=1,dp[2]=2,dp[3]=4;
       //填表
       for(int i=4;i<=n;++i)  dp[i]=((dp[i-1]+dp[i-2])%MOD+dp[i-3])%MOD;
       return dp[n];
    }
};

思路2：dp[i]表示从i位置到达终点一共有几种方法

class Solution {
public:
    int waysToStep(int n) 
    {
        const int MOD=1e9+7;
       //边界情况
       if(n==1||n==2) return n;
       if(n==3) return 4;
       //建立dp表
       vector<int> dp(n);
       //初始化
       dp[n-1]=1,dp[n-2]=2,dp[n-3]=4;
       //填表
       for(int i=n-4;i>=0;--i)  dp[i]=((dp[i+1]+dp[i+2])%MOD+dp[i+3])%MOD;
       return dp[0];
    }
};

三、使用最小的花费爬楼梯

. - 力扣（LeetCode）使用最小的花费爬楼梯

方法1：dp[i]表示从起点到i台阶的最小花费

class Solution {
public:
    int minCostClimbingStairs(vector<int>& cost) 
    {
        int n=cost.size();
        vector<int> dp(n+1);
        //开始填表
        for(int i=2;i<=n;++i) dp[i]=min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);
        return dp[n];
    }
};

思路2：我们也可以以i为起点，让dp[i]表示到楼顶的最小花费

class Solution {
public:
    int minCostClimbingStairs(vector<int>& cost) 
    {
        int n=cost.size();
        //处理边界情况
        
        vector<int> dp(n);
        dp[n-1]=cost[n-1],dp[n-2]=cost[n-2];
         for(int i=n-3;i>=0;--i) dp[i]=cost[i]+min(dp[i+1],dp[i+2]);
         return min(dp[0],dp[1]);
    }
};

四、解码方法

. - 力扣（LeetCode）解码方法

class Solution {
public:
    int numDecodings(string s) 
    {
       int n=s.size();
       vector<int> dp(n);
       if(s[0]!='0') ++dp[0];
       //处理边界情况
       if(n==1)  return dp[0];
       if(s[1]!='0'&&s[0]!='0') dp[1]++;
       int t=(s[0]-'0')*10+(s[1]-'0');
       if(10<=t&&t<=26) ++dp[1];
       //开始填表
       for(int i=2;i<n;++i) 
          {
            if(s[i]!='0') dp[i]+=dp[i-1];
            int t=(s[i-1]-'0')*10+(s[i]-'0');
            if(10<=t&&t<=26) dp[i]+=dp[i-2];
          }
          return dp[n-1];
    }
};

       我们会发现dp[1]的初始化和填表里面的过程非常相似，所以我们可以用一个动态规划的小技巧——虚拟节点（专门用来处理边界问题）

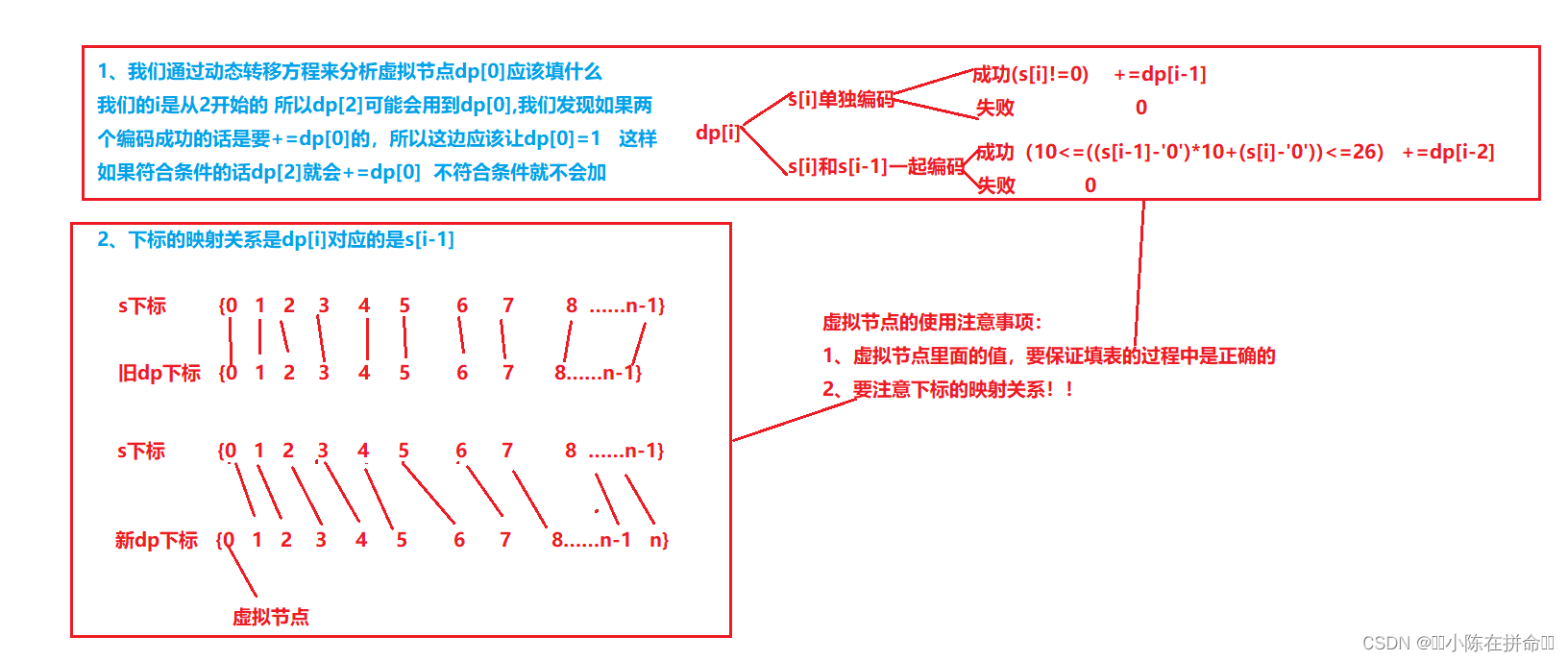
class Solution {
public:
    int numDecodings(string s) 
    {
       int n=s.size();
       vector<int> dp(n+1);
       dp[0]=1;
       if(s[0]!='0') ++dp[1];
       //开始填表
       for(int i=2;i<=n;++i) 
       {
         if(s[i-1]!='0') dp[i]+=dp[i-1];
         int t=(s[i-2]-'0')*10+(s[i-1]-'0');
         if(10<=t&&t<=26) dp[i]+=dp[i-2];
       }
       return dp[n];
    }
};

当然如果觉得这样对齐太麻烦了 字符串有一个技巧就是可以在前面加一个空格

class Solution {
public:
    int numDecodings(string s) {
        //dp[i]表示以i位置为结尾时可以编码的组合总数
        //s[i]单独编码时 if(s[i]!=0) +=dp[i-1] 
        //s[i]和s[i-1]组合编码的时候 if(10<((s[i-1]-'0')*10+s[i]-'0')<26)  +=dp[i-2]
        int n=s.size();
        s=' '+s;//字符串技巧
        vector<int> dp(n+1);
        dp[0]=1,dp[1]=(s[1]!='0');
        //dp[1] 的情况 1、两个都单独编码成功 +1 2、一起编码成功 +1
        for(int i=2;i<=n;++i)
        {
         if(s[i]!='0') dp[i]+=dp[i-1];
         int t=((s[i-1]-'0')*10+s[i]-'0');
         if(10<=t&&t<=26) dp[i]+=dp[i-2];
         }
         return dp[n];
    }
};

 先暂时更新到这，后面有新的题目会持续更新