1. 题目链接

OJ链接 : 岛屿的最大面积 

2. 题目描述

给你一个大小为 m x n 的二进制矩阵 grid 。

岛屿 是由一些相邻的 1 (代表土地) 构成的组合，这里的「相邻」要求两个 1 必须在 水平或者竖直的四个方向上 相邻。你可以假设 grid 的四个边缘都被 0（代表水）包围着。

岛屿的面积是岛上值为 1 的单元格的数目。

计算并返回 grid 中最大的岛屿面积。如果没有岛屿，则返回面积为 0 。

 

示例 1：

 

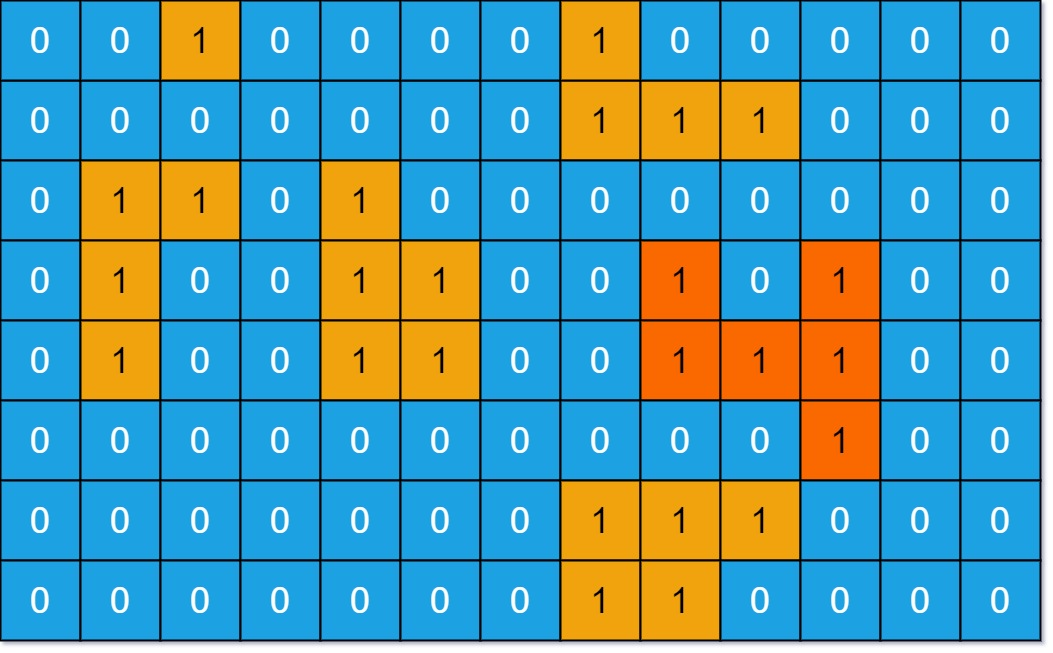
输入：grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]]
输出：6
解释：答案不应该是 11 ，因为岛屿只能包含水平或垂直这四个方向上的 1 。

示例 2：

输入：grid = [[0,0,0,0,0,0,0,0]]
输出：0

 

提示：

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 50
• grid[i][j] 为 0 或 1

3. 解法

算法思路:

遍历整个矩阵, 每当遇到一块土地的时候, 就用 [深搜] 或者 [宽搜] 将与这块土地相连的 [整个岛屿] 的面积计算出来

然后在搜索得到的 [所有岛屿面积] 求一个 [最大值] 即可.

在搜索的过程中, 为了 [防止搜到重复的土地] : 

1. 可以开一个同等规模的 [布尔数组] , 标记一下这个位置是否已经被访问过

2. 也可以将原始矩阵的1修改成0, 但是这样操作会修改原始矩阵

我们这里还是选择最优解第一种方法, 当然我们笔试可以使用第二种, 只要过了就好, 但是我们面试的时候, 尽量要拿出最优解~

代码展示:

class Solution 
{
    int dy[4] = {1, -1, 0, 0};
    int dx[4] = {0, 0, 1, -1};
    typedef pair<int, int> PII;
    bool vis[51][51];
    int n, m;

public:
    int maxAreaOfIsland(vector<vector<int>>& grid)
    {
        n = grid.size(), m = grid[0].size();
        int ret = 0;
        for(int i = 0; i < n; i++)
        {
            for(int j = 0; j < m; j++)
            {
                if(grid[i][j] == 1 && !vis[i][j])
                {
                    ret = max(ret, bfs(grid, i, j));
                }
            }
        }
        return ret;    
    }

    int bfs(vector<vector<int>>& grid, int i, int j)
    {
        int count = 0;
        queue<PII> q;
        q.push({i, j});
        vis[i][j] = true;
        count++;
        
        while(q.size())
        {
            auto [x, y] = q.front();
            q.pop();
            for(int k = 0; k < 4; k++)
            {
                int a = dx[k] + x, b = dy[k] + y;
                if(a >= 0 && a < n && b >= 0 && b < m && grid[a][b] == 1 && !vis[a][b])
                {
                    q.push({a, b});
                    vis[a][b] = true;
                    count++;
                }
            }
        }
        return count;
    }
};

 

4. 算法总结

时间复杂度
最坏情况下，算法的时间复杂度为 O(n* m)，其中 n 是行数，m 是列数，因为每个单元格最多只会被访问一次。
空间复杂度
空间复杂度为 O(n* m)，用于存储访问状态数组 vis 和队列 q 的空间。
总结
该算法有效地利用了 BFS 方法遍历整个网格，以找出所有岛屿的面积，最终返回最大的岛屿面积。它是处理图形（在本例中为网格）相关问题的经典方法之一，特别适合用于寻找连通分量。