核心思想
TimSort的核心思想是充分利用数据中已有的顺序(降序,升序)来减少比较和置换的操作次数。
所以用数据的分区和合并都做了很多细节优化。
基于插入排序对小数组表现良好的事实,因此在最好情况下可以获得插入排序 o(n)的最好性能。同时又能获得归并排序最差o(nlogn)的性能表现。
排序算法性能概览
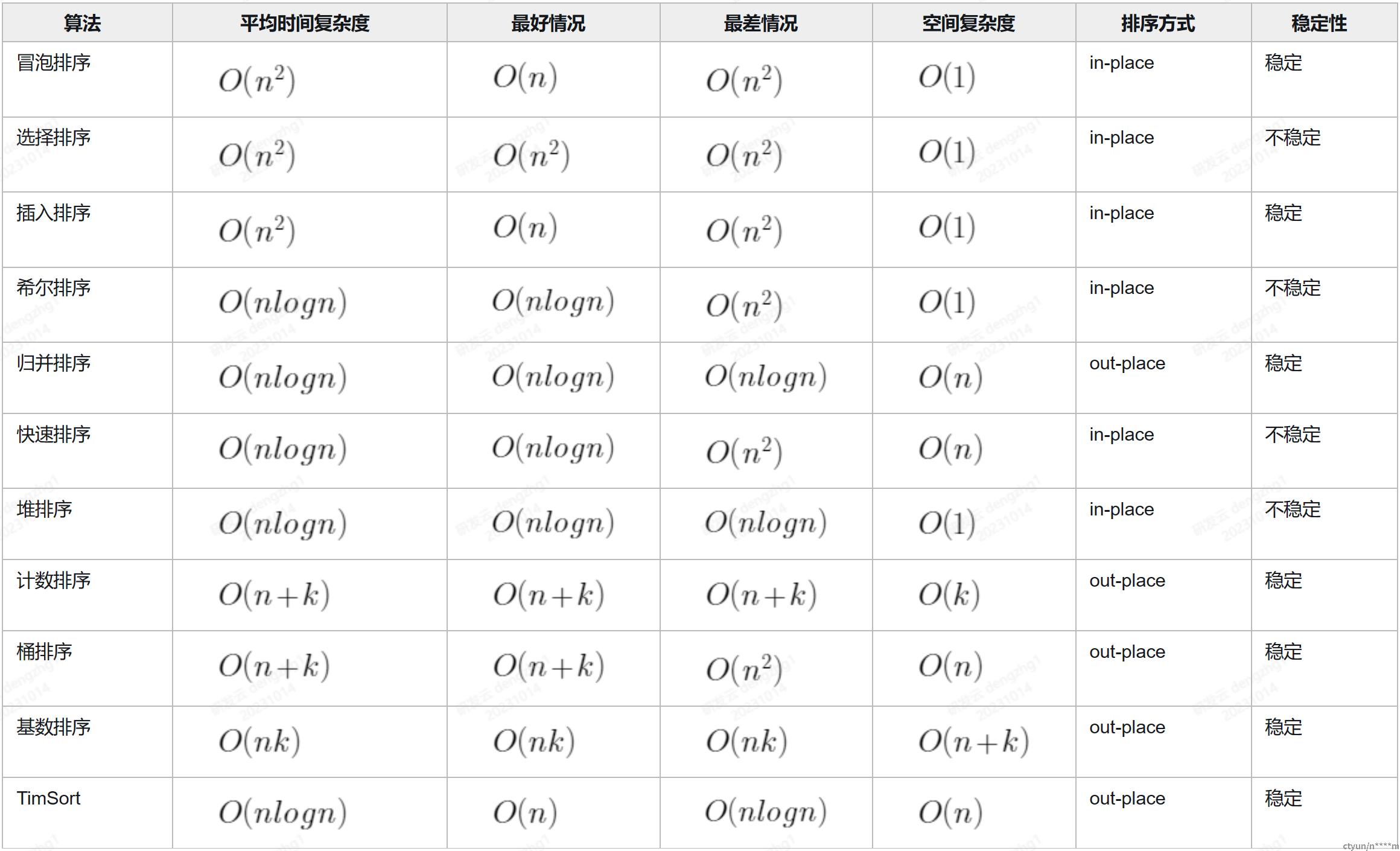
算法详解
执行过程
首先根据,需要排序的区间长度,如果区间长度小于 MIN_MERGE,使用binarySort排序;否则使用归并排序。
MIN_MERGE 在Java中定义为常数32。
从左到右遍历一遍被排序数组;找到自然的“分区”, 如果自然分区的长度小于 minRun,则扩展到 minRun 长度,然后将这个自然分区
归并到栈中,直到剩余的区间长度为0,结束。
分区
分区就是下一次扫描过程中,找出的“自然排序”的一个区间。它需要满足下面两个条件之一:
- 非降序
a0 <= a1 <= a2 <= ...
- 严格降序
a0 > a1 > a2 > ...
这么定义的原因是保证稳定性;对于严格降序的序列,会使用swap翻转转换为升级序列,严格降序保证了翻转的过程中,不改变相等元素的位置,即稳定性。
分区长度选择 minRun
设N为需要排序的区间长度; 假如N< MIN_MERGE,不需要归并。如果N是2的幂,那么选择分区长度为 16,32,64,128的性能测试相差不大。
如果N不是2的幂,可能会遇到如下的情况。
考虑 N = 2112, 则
divmod(2112, 32) (66, 0)
则前面64个分区正好合并,剩余最后需要把64长度区间,与1024区间合并,也就是接近需要移动接近 o(N) 数据,仅仅为了把剩余的64个元素归并到合适位置。
所以对于分区长度的计算,保证 N/minRun 或者等于2的幂,或者< 某个2的幂。
当待排序的数据很随机,而每个自然分区的长度都小于minRun的情况下(自然分区长度大于minRun就不会按照minRun延申长度了),这样保证归并的时候,两个序列的长度不至于相差很大。
Java 中使用下面方法来计算,minRun,也就使用minRun来遍历切分数组,构造分区。
/**
* Returns the minimum acceptable run length for an array of the specified
* length. Natural runs shorter than this will be extended with
* {@link #binarySort}.
*
* Roughly speaking, the computation is:
*
* If n < MIN_MERGE, return n (it's too small to bother with fancy stuff).
* Else if n is an exact power of 2, return MIN_MERGE/2.
* Else return an int k, MIN_MERGE/2 <= k <= MIN_MERGE, such that n/k
* is close to, but strictly less than, an exact power of 2.
*
* For the rationale, see listsort.txt.
*
* @param n the length of the array to be sorted
* @return the length of the minimum run to be merged
*/
private static int minRunLength(int n) {
assert n >= 0;
int r = 0; // Becomes 1 if any 1 bits are shifted off
while (n >= MIN_MERGE) {
r |= (n & 1);
n >>= 1;
}
return n + r;
}
合并模式
在扫描的过程中,可能出现各种混合长度的分区,在算法稳定性的约束下,可行的合并必须发生在相邻的两个分区。
例如,我们有连续的三个分区, A B C, 合并的模式必须是 (A+B)+C 或者 A+(B+C)。
当我们找到一个自然分区时,先把它的起始位置和长度压入栈中,然后调用 mergeCollapse() 进行merge直到下面的条件满足:
假设A B C是最右边的连续3个尚未合并的分区的长度,我们保证下面两个条件:
1. A > B + C
2. B > C当 A <= B+C时,A和C较小的一个会跟B合并;当A=C时,B和C合并可以更好利用缓存。
若合并之后上面的条件不满,则继续进行合并直到栈中没有3个以上分区或者条件满足。
合并算法
假设A, B分别是相邻的两个带合并的分区长度, In-place的合并算法很复杂;但是在允许使用min(A,B)临时空间的情况下,是比较容易实现的。
merge_lo() 处理当A<=B的情况;merge_hi() A>B。
合并算法的基本就是经典的一一比较的合并,TimSort中增加了驰骋模式的优化(galloping mode)。简单来说,
就是在一对一比较的同时,我们计数,记录“winner”来自同一个分区的次数,当计数超过了设定的阈值
min_gallop,则进入slice的拷贝模式,直到计数小于min_gallop,退回到一对比较模式。
min_gallop的初始值也来源于实际观察,目前java中它的初始值MIN_GALLOP=7。
Galloping Mode
在Galloping Mode中,算法在一个run中搜索另一个run的第一个元素。通过将该初始元素与另一个run的第 2k-1个元素(即1,3,5...) 进行比较来完成,以便获得初始元素所在的范围。这样缩短二分查找的范围,在某些数据中可以提高效率。
为了避免Galloping mode的缺点,合并函数会调整阈值。如果所选元素来自先前返回元素的同一个run, 则min_gallop减1,否则,min_gallop增加1,从而阻止返回到Galloping mode。在随机数据的情况下,min_gallop的值会变得非常大,以至于Galloping mode永远不再发生。
TimSort也是java 7以上的默认排序算法,它的算法性能优秀,思想和代码都值得阅读。
参考
-
geekforgeeks timsort
-
java/util/ComparableTimSort.java