一.树结构之二叉树操作
二叉树的查找
二叉搜索树,也称二叉排序树或二叉查找树
二叉搜索树:一棵二叉树,可以为空,如果不为空,应该满足以下性质:
- 非空左子树的所有结点小于其根结点的键值
- 非空右子树的所有结点大于其根结点的键值
- 左右子树都是二叉搜索树
对于二叉树的查找,其实沿用的是分治法的思想,所以我们的树一定是要排序好的,这样才能使用每次检索都少一半的数据量
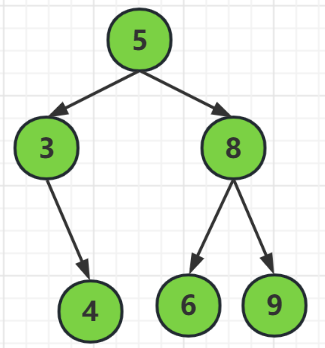
我们可以看到上面的二叉树,它满足根结点的左边都比根结点小,而右边又都比根结点大,所以它就是可以使用二叉树查找的
当我们要查找6时
首先,我们对根节点进行比较,发现6是大于5的所以,我们需要去根结点的右边也就是结点8
然后,结点8进行对比,发现它比结点8小,所以去结点的额左边也就是结点6
最后,结点6和查找键值6是一样的,所以找到了
以下是代码实现:
Position Find(ElementType x, BinTree BST) { if (!BST) { return NULL; } if (x > BST->Data) { return Find(x, BST->Right); } else if (x<BST->Data){ return Find(x, BST->Left); } else{ return BST; } }
我们可以发现,使用递归实现的代码查找,其实是尾递归,对于尾递归,我们可以直接使用循环来做
利用循环的代码实现:
//将尾递归转换为循环,效率高 Position IterFind(ElementType x, BinTree BST) { while (BST) { if (x > BST->Data) { BST = BST->Right; } else if(x<BST->Data){ BST = BST->Left; } else return BST; } return NULL; }
二叉树的插入
插入结点的关键在于要找到结点的位置,我们可以使用查找函数的思维,找到它的位置,然后再对应插入
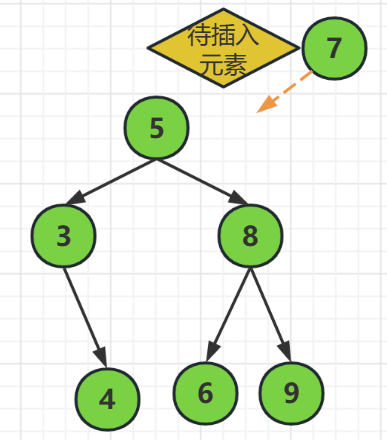
上面的图片,我们要插入元素7到树中去,
首先,元素7是大于根节点5的,所以元素7应该处于根结点的右边位置,就和结点8进行比较
然后,发现结点8是大于元素7的,所以我们元素7因该在结点8的左边,也就是到了结点6的位置,
最后,结点6左右无元素,且元素7大于结点6,所以元素7位于结点6的右子结点
然后是代码实现:
BinTree Insert(ElementType x, BinTree BST) { if (!BST) { BST = malloc(sizeof(struct TreeNode)); BST->Data = x; BST->Left = BST->Right = NULL; } else { if (x < BST->Data) { BST = Insert(x, BST->Left); } else if (x>BST->Data) { BST = Insert(x, BST->Right); } return BST; } }
二叉树的删除
删除的情况要复杂一些,因为我们的树分有子结点和无子结点,当然无子结点的肯定是很好删除的,主要是有子结点的怎么删除呢?
这就需要我们分情况讨论:
无子结点时:
直接删除需要删除的结点,并修改其父结点的指针,置为NULL
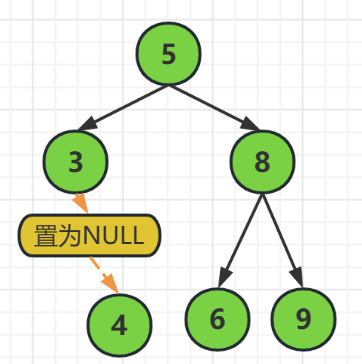
如上图,
当我们要删除结点4的时候,结点4自己是没有子结点的,
所以我们可以直接释放结点4,并且把结点3的右结点指针指向NULL
当有一个子结点的时候:
需要把要删除的结点的父结点指针,指向它的孩子结点,相当于中间少了一层
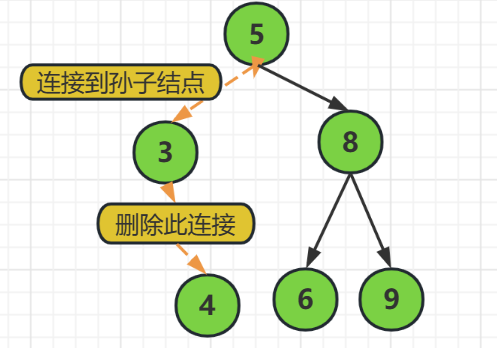
如上图,
我们要删除结点3的时候,发现它是有一个结点4的,我们就不能直接把结点3删除了
而是要先把结点5的指向结点3的指针指向结点4
然后再释放结点3
当有两个子节点的时候:
这种情况使用的方法是,要么使用左子树的最大元素顶上去,要么使用右子树的最小元素顶上去
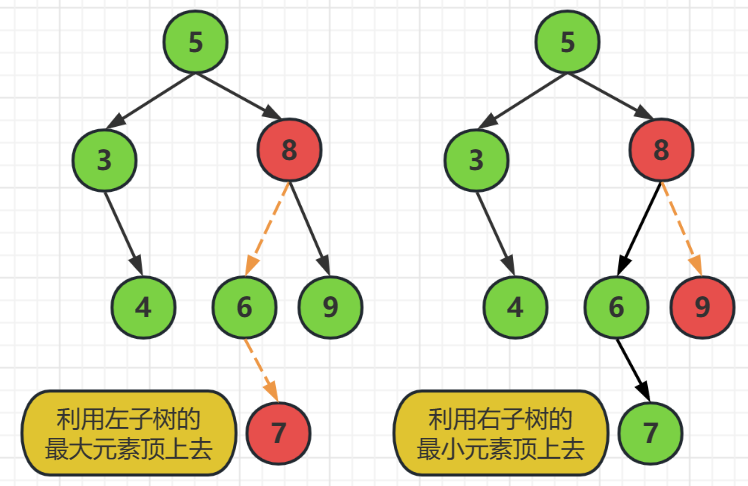
这里需要删除的结点是8,
我们可以在左子树中去找到最大的元素,然后替换到结点8的值,然后删除结点7就可以了
还可以去右子树中找到最小的元素,然后替换掉结点8为最小结点的值,然后删除最小结点
注意:
删除结点时需要改变父结点指针指向为NULL
当删除的结点后面还有结点时,要一个一个的连接到前面来
然后就是代码实现:
// 查找最小结点 Position FindMin(BinTree BST) { if (!BST) return NULL; else if (!BST->Left) return BST; else { return FindMin(BST->Left); } } //删除结点 BinTree Delete(ElementType x, BinTree BST) { Position Temp; if (!BST) printf("要删除的元素未找到!"); else if (x < BST->Data) { BST->Left = Delete(x, BST->Left); //在左子树查找要删除的元素 } else if (x > BST->Data) { BST->Right = Delete(x, BST->Right); //在右子树查找要删除的元素 } else //找到要删除的结点 { if (BST->Left && BST->Right){ //左右都有结点 Temp = FindMin(BST->Right); //找右子树的最小元素 BST->Data = Temp->Data; //把右子树最小元素覆盖到要删除的元素上 BST->Right = Delete(BST->Data, BST->Right); //删除右子树的最小元素 } else {// 只有一个结点的情况,或没有结点的情况 Temp = BST; if (!BST->Left) { //右结点存在,或没有结点存在 BST = BST->Right; } else if (!BST->Right) { //左结点存在,或没有结点存在 BST = BST->Left; } free(Temp); } } return BST; }
二.进阶之平衡二叉树(AVL树)
什么是平衡二叉树?
平衡二叉树(AVL树):空树,或者任一结点左,右子树的高度差绝对值不超过1,即| BF(T)<=1 |
平衡因子:BF(T) = hL - hR ,其中hL,hR是T的左子树高度和右子树高度
我们可以来看几个图分别一下是不是平衡二叉树:
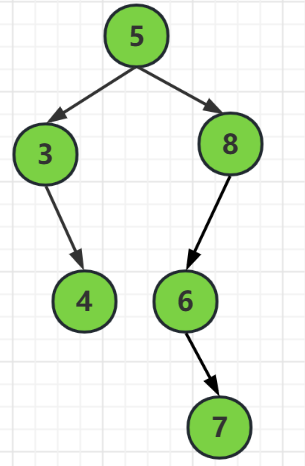
上图,对于结点5来说,左子树高度2,右子树高度3
3 - 2 = 1 满足 | BF(T)<= 1 |
但是对于右子树的结点8来说,它的左子树高度是2,右子树高度为0
2-0 = 2就不满足 | BF(T)<= 1 |
所以这不是一棵平衡二叉树
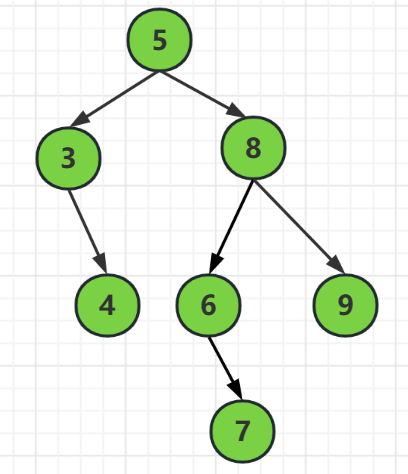
对于这颗树来说,
结点5 的左子树高度是2,右子树高度是 3,满足最小高度为小于等于 1
结点8 的左子树高度是2,右子树高度是1,满足最小高度为小于等于 1
所以它是一棵平衡的二叉树
平衡二叉树的调整
平衡二叉树在建树的时候其实是平衡的,主要是在后期的插入和删除中,会破坏掉它的平衡,最常见的就是插入就破坏了平衡,即 | BF(T)> 1 | ,它就不满足平衡二叉树了
所以我们在插入的时候,会有一个二叉树的平衡调整的过程
RR旋转(右单旋转)------
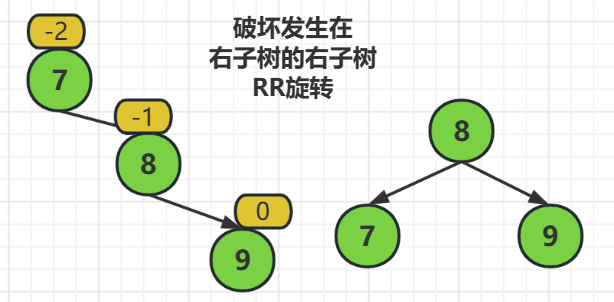
RR旋转指的就是,破坏发生在右子树的右子树,
解决方式就是把被破环的结点,也就是结点7的右子树作为它们的父结点,相当于把结点7提起来做父结点
由于我们的平衡二叉树在调整的时候也需要注意满足查找二叉树的准则,所以对被提起来的结点,它左边的结点需要挂到它父结点的左边
也就是说,把结点8做父结点提起来的时候,结点8的左子树要挂在结点7的右边
LL旋转(左单旋转)------
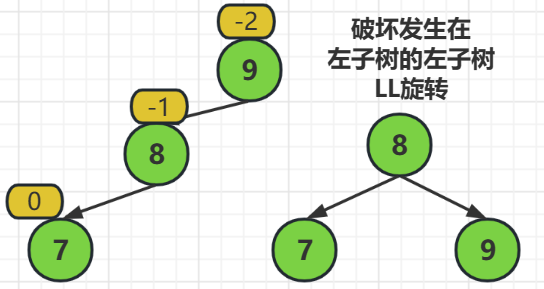
LL旋转指的是,破坏发生在左子树的左子树
解决方式就是把被破坏的结点的子结点,提起来当作父结点,而原来的父结点当作子结点
也就是结点8被当作父结点,而原来的结点7被落下去当子结点了
由于平衡二叉树在被调整以后依然要满足查找二叉树的准则,所以我们需要把被提起来的结点的右子树,放在落下去结点的左子树
也就是,原来结点8的右子树要放在现在结点9的左子树(存在的情况下)
LR旋转 ----------
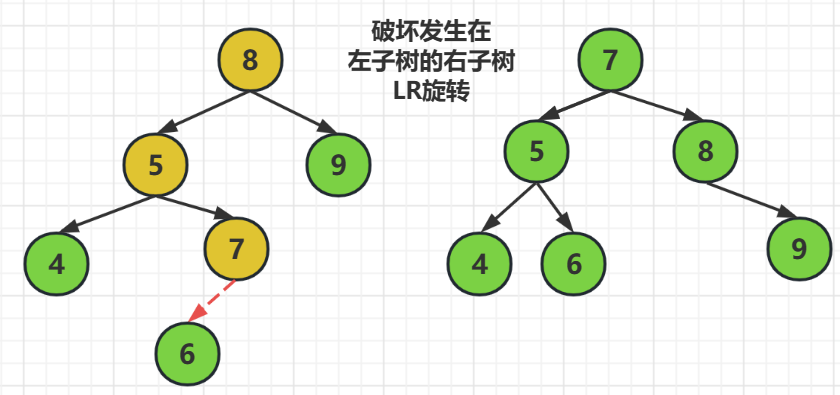
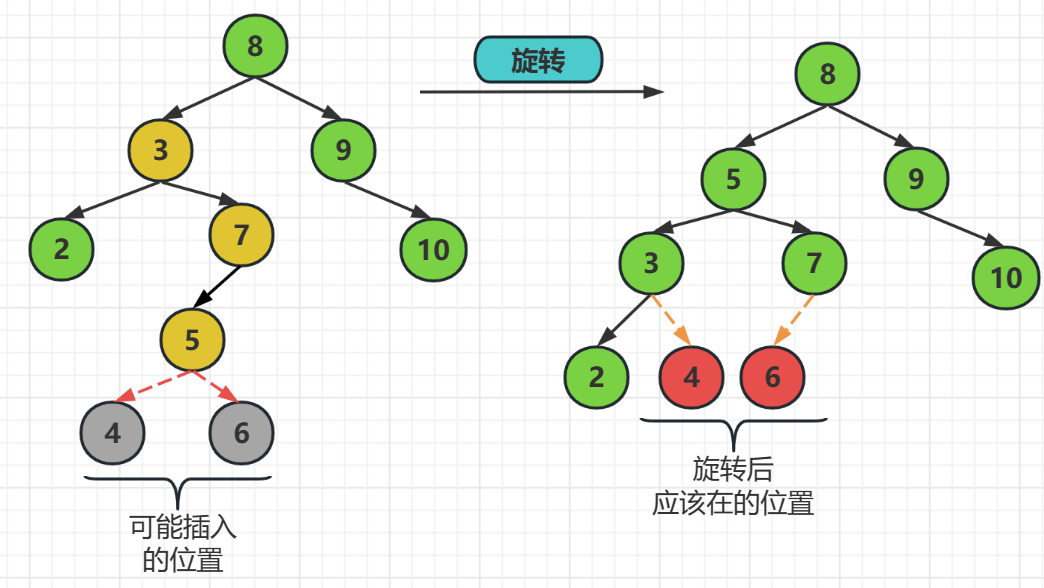
LR旋转指的是,破坏发生在左子树的右子树上
解决方式就是发生把发生破坏的结点提起来左父结点,而原来的左子树结点继续做左子树结点,原来的父结点做右结点
注意这时的波坏结点可能是插入了结点的,如果它插入在左边,那么他就是原来左子树结点的右子树,如果它插在破坏结点的右边,那么它就应该在原父结点的左边
也就是,在结点8,结点5,结点7中,结点7要被提起来做父结点,结点5继续做它的左子树结点,而原来的父结点8做新父结点的右子树
对于新插入的元素6,由于它是插入在结点7的左边,所以它是结点5的右子树,当然他要是插在了结点7的右边,那么它就是结点8的左子树
解释如下:
RL旋转 ---------
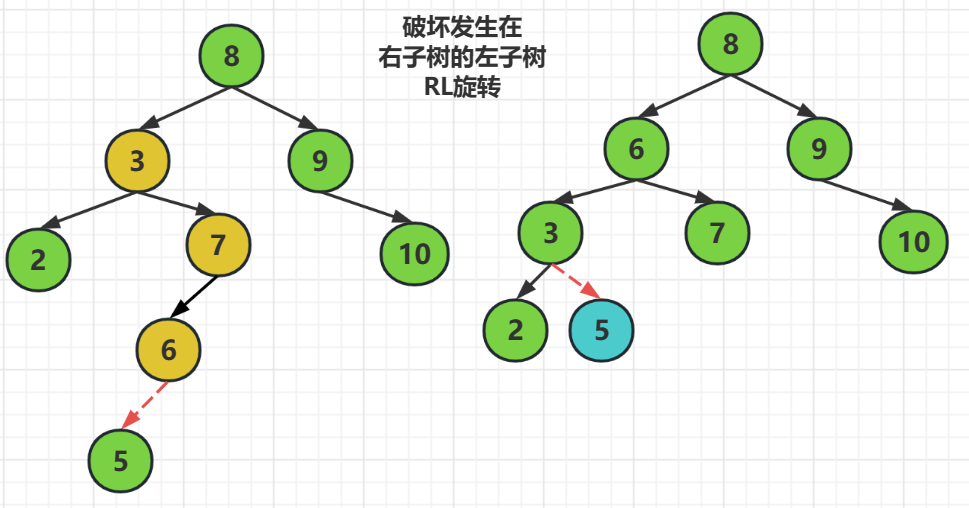
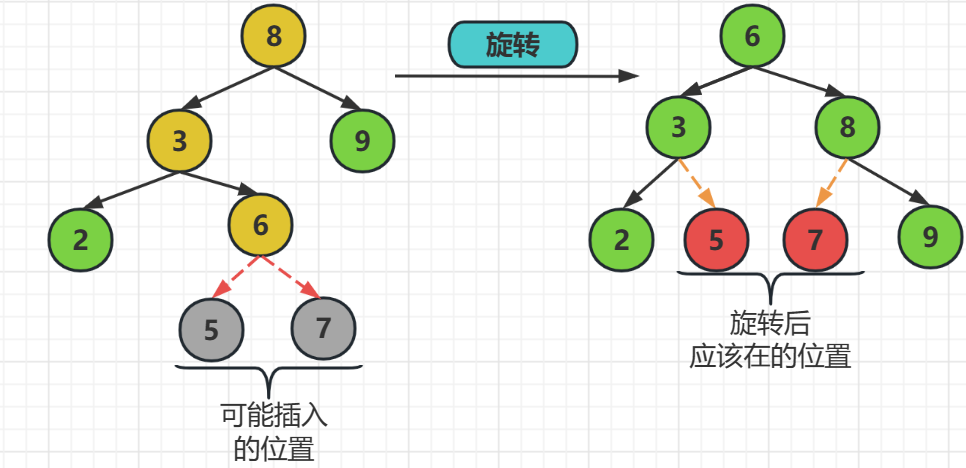
RL旋转指的就是,破坏在右子树的左子树
解决方式就是把破坏结点提起来做父结点,原来的父结点做新父结点的左子树,而原来的右子树还是新父结点的右子树
由于我们平衡二叉树调整后还要满足查找二叉树,所以对于插入破坏结点左边的数要在新的左子树的右边,而插入到破坏结点右边的数要在新的右子树的左边
也就是,把结点6提起来做新的父结点,原父结点3做结点6的左子树,而右结点则还是结点7,
对于原来插入到结点6左边的数要在新的左子树3的右边,而插入在结点6的右边的,要在新的右子树的左边
解释如下:
三.树的应用
对于一棵二叉树来说,它可以有多个输入序列,但是,构成的可能是同一棵二叉树,那么我们怎么根据输入序列来判断是不是同一棵二叉树呢?
不建树的判别方法:
如 :
3,1,2,4
vs
3,4,1,2
由于第一个元素肯定是根结点,所以根结点就是3,并且比根结点小的在左边,比它大的在右边
所以被分成了
{1,2} ,3,{4}
{1,2} ,3,{4}
我们可以看到它们此时的序列是完全一样的,所以可以构成一棵二叉树
在如:
3,1,2,4
vs
3,2,4,1
一样的方法划分,3为根结点
{1,2},3,{4}
{2,1},3,{4}
对于左边来说,第一个元素是下一层的根结点,
所以一个是1为父结点,一个是2为父结点,显然不是同一颗二叉树
建一棵二叉树,其它序列来依次对比:
typedef struct TreeNo* Tree; struct TreeNo { int v; Tree Left, Right; int flag; };
这是我们需要使用到的结构
我们对于多个输入序列,只会构建一棵二叉树,然后就是让序列 对已经构建好的二叉树进行遍历,其中flag有重要的作用
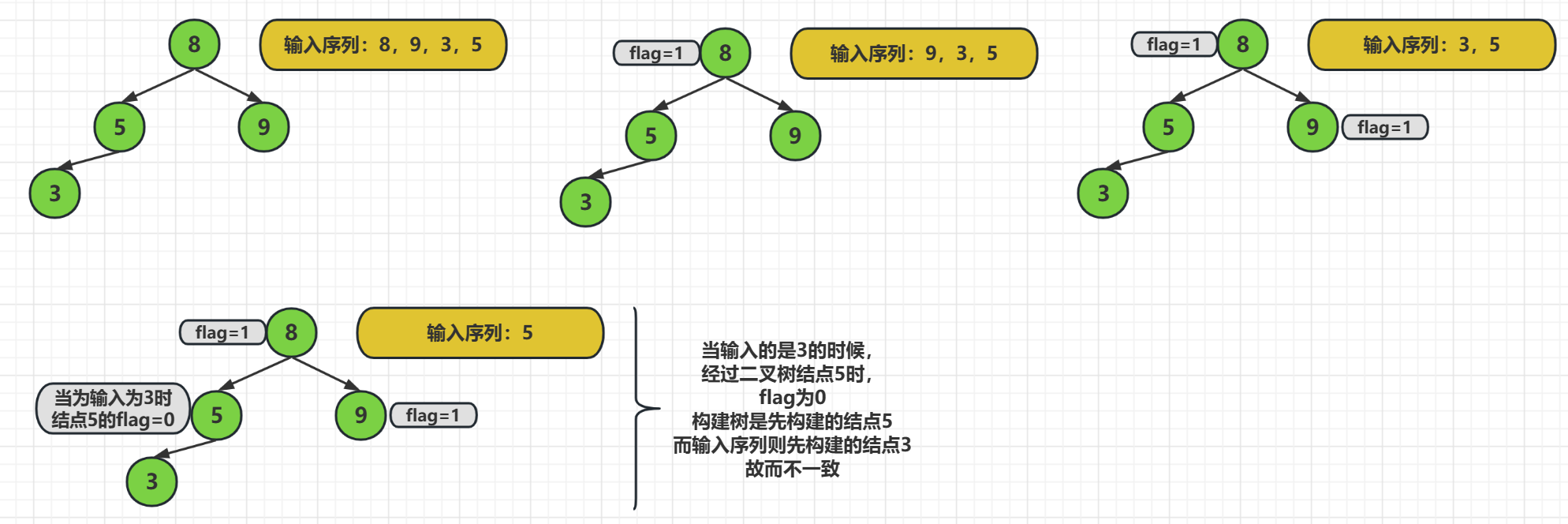
这种方法来判定二叉树是否同构的思想是,
我们已经构建好了一棵二叉树,然后只需要对输入序列依次访问,
如果被访问的结点flag为0,那么就给flag赋值为1,
如果不是被访问结点,但是访问过了也就是flag为1,那么可以向下寻找,
如果不是被访问的结点,但是flag也不为1,那么则表示不同构
原因是,它们两个结点的构建的位置不一样,可以看上面的图片,输入序列要先构建3为父结点,而已构建的二叉树则使用结点5作为父结点,说以两个二叉树不同构
四.红黑树--拓展
红黑树(Red Black Tree) 是一种自平衡二叉查找树,是在计算机科学中用到的一种数据结构,典型的用途是实现关联数组
红黑树的特性:
- 根结点是黑色的
- 叶子结点(null值)黑结点
- 红结点的子结点必须是黑结点
- 新插入的结点是红色的结点
- 父结点到任一叶子结点黑结点数相同
红黑树也是一种自平衡的二叉树,但是它比二叉平衡树的条件更加宽泛,
二叉平衡树所要求的平衡是左子树和右子树的高度相差小于等于1
而红黑树的要求是父结点到叶子结点的黑节点数相同就可以了,这个条件其实是很宽泛的了,我们可以找出它的一种极端情况,那么就是左子树都是黑色,而右子树黑红交叉,
这种情况构建的红黑树,它右半边的结点数其实是左边的2n-1
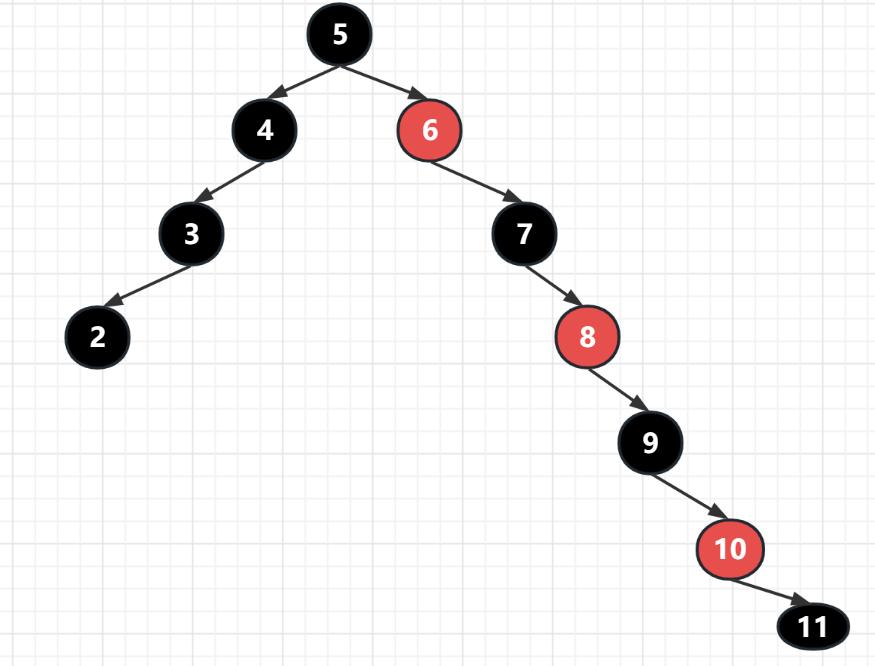
假如有一颗这样的树,其实不存在,因为很多右子树,左子树都没数据,是构成不了红黑树的,
我们看到它左边的长度是3,而右边则是6,很显然比左边多出了一倍,那么还能叫自平衡树吗?
这就是红黑树的平衡,我们可以把红结点都去掉,发现黑节点其实是平衡的,更重要的是,就算加上红结点,其实上面的查找的时间复杂度也是O(2 * log2 n)
由于我们的常量是不用记录到时间复杂度的,所以依旧是 log2 n
所以红黑树给出的平衡指的是:左子树和右子树的结点相等或相差一倍,都是可以的
为什么红黑树这样定义平衡呢?
我们可以直到AVL二叉树它的平衡过于严格,所以每次插入都可能有很大的变化,大多数插入的时间都花在了维持那严格的平衡上了
而宽泛的红黑树,则变动更少,它的平均性能又很高,它能保证很高的性能,而又插入不会频繁的发生变更,所以红黑树就使用自己定义的那套平衡机制
红黑树的构造过程:
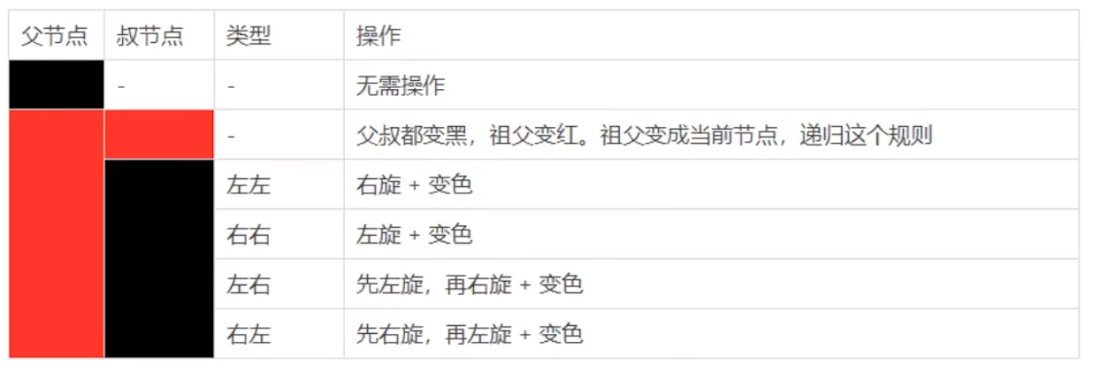
上面的图片就是红黑树的构造规则,我们可以简单的来实现一下: