二分查找

二分查找

没啥可说的,轻轻松松~

class Solution {
	public int search(int[] nums, int target) {
		int left = 0;
		int right = nums.length - 1;
		while (left <= right) {
			int mid = (right + left) / 2;
			if (nums[mid] > target) {
				right = mid - 1;
			} else if (nums[mid] < target) {
				left = mid + 1;
			} else {
				return mid;
			}
		}
		return -1;
	}
}

在排序数组中查找元素的第一个和最后一个位置

可以使用二分查找.

查找左端点:

• 把区间划分成两个部分, 1. num[mid] < t , num[mid] >= t .
  把区间划分成 num[mid] < t 和 num[mid] > t ,这谁都懂,就不说了.
  关键是 “=” 给谁? 左边还是右边?
  关于为啥给右边,这里就不说了.
  我在这里只是讲一个记忆方法(左右都适用):
  求左端点,只看左括号,哪个括号在中间,“=” 就给谁.
  具体如下:
• 划分好区间,接下来就要想指针的移动方式了.
  

查找右端点:

• 把区间划分成两个部分, 1. num[mid] <= t , num[mid] > t .
  “=” 给谁,参考上面的记忆方法.

  • 求右端点,只看右括号,哪个括号在中间,“=” 就给谁.

• 指针的移动方式,跟查找左端点的方法类似,自己写写试试~

class Solution {
    	public int[] searchRange(int[] nums, int target) {
		int[] ret = {-1, -1};
		if (nums.length == 0)
			return ret;
		int left = 0;
		int right = nums.length - 1;
		int mid = 0;
		while (left < right) {
			mid = left + (right - left) / 2;
			if (nums[mid] < target) {
				left = mid + 1;
			} else {
				right = mid;
			}
		}

		if (nums[left] == target)
			ret[0] = left;
		else
			return ret;
			
		right = nums.length - 1;
		while (left < right) {
			mid = left + (right - left + 1) / 2;
			if (nums[mid] <= target) {
				left = mid;
			} else {
				right = mid - 1;
			}
		}
		ret[1] = left;
		return ret;
	}

}

坑:

• nums 数组的长度可能为0.
• 二分没写好,容易死循环.

我在写完以后,有个疑问:

• 为啥循环结束后 mid 指向的值,不是我们想要的?

确实困惑了我一会,不过后来一想就明白了,因为出循环后 mid 差一次更新 ( left 或 right已经变了,但是 mid 没有变).

搜索插入位置

用查找左端点的方法,秒了~

坑:

• 注意边界情况 nums[nums.length-1] < target.

class Solution {
    public int searchInsert(int[] nums, int target) {
        if(nums[nums.length-1] < target) return nums.length;
        int left=0,right=nums.length-1;
        while(left < right) {
            int mid = left+(right-left)/2;
            if(nums[mid] < target) {
                left = mid + 1;
            } else if(nums[mid] >= target){
                right = mid;
            }
        }
        return right;
    }
}

用左端点做完以后,我想了想,为啥不能用右端点做呢?
确实困扰了我一会,后来明白了,题目要查找的值是要 >= target 的.
而使用查找右端点的方法,会漏掉 > target 的情况: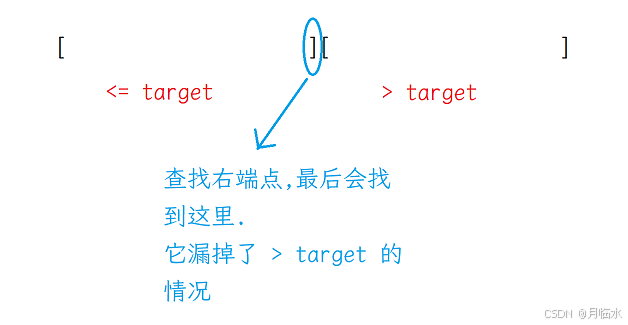

x 的平方根

分析一下,可以把区间划分成 mid*mid <= x 和 mid*mid > x.一看就是右端点,秒了~

坑:

• 数值过大,要用 long 类型.

class Solution {
    	public int mySqrt(int x) {
		long left = 0, right = x;
		while (left < right) {
			long mid = left + (right - left + 1) / 2;
			if (mid * mid <= x) {
				left = mid;
			} else {
				right = mid - 1;
			}
		}
		return (int) left;
	}
}

山脉数组的峰顶索引

没想到怎么把数组划分成两部分.
也就是 if(...) 中的条件不会写.

看了看题解,没想到还能这样做.
以 arr[mid - 1] < arr[mid] 划分~

class Solution {
    public int peakIndexInMountainArray(int[] arr) {
        int left = 0, right = arr.length - 1;
        while (left < right) {
            int mid = left + (right - left + 1) / 2;
            if (arr[mid - 1] < arr[mid]) {
                left = mid;
            } else {
                // 前面括号内有 +1 ,这里就 -1 .
                right = mid - 1;
            }

        }
        return left;
    }
}

寻找峰值

画图不能偷懒,要老老实实的画,写全了~

	public int findPeakElement(int[] nums) {
		int left = 0;
		int right = nums.length - 1;
		while (left < right) {
			int mid = left + (right - left) / 2;
			if (nums[mid] < nums[mid + 1]) {
				left = mid + 1;
			} else {
				right = mid;
			}
		}
		return left;
	}

寻找旋转排序数组中的最小值

没想出来,题解是用 n-1 这个位置的数来划分区间的.

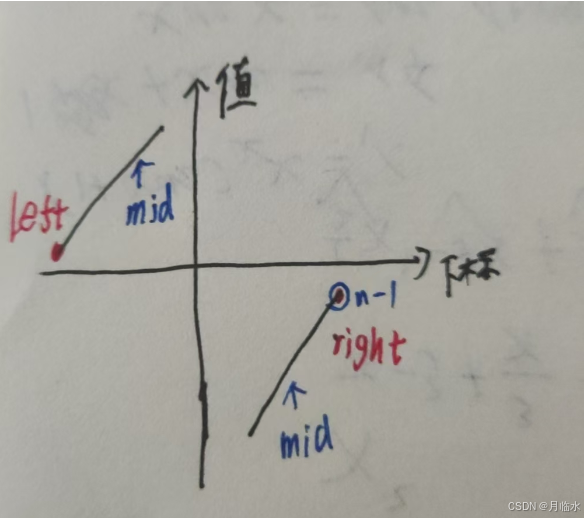
	public int findMin(int[] nums) {
		int left = 0;
		int right = nums.length - 1;
		while (left < right) {
			int mid = left + (right - left) / 2;
			if (nums[mid] < nums[nums.length - 1]) {
				right = mid;
			} else {
				left = mid + 1;
			}
		}
		return nums[right];
	}

下面这个是用 0 位置来划分区间的(需要考虑一个特殊情况~).

	public int findMin(int[] nums) {
		int left = 0;
		int right = nums.length - 1;
		if (nums[0] < nums[nums.length - 1]) {
			return nums[0];
		}
		while (left < right) {
			int mid = left + (right - left) / 2;
			if (nums[mid] < nums[0]) {
				right = mid;
			} else {
				left = mid + 1;
			}
		}
		return nums[right];
	}

点名

写出来了,用的二分~

class Solution {
    public int takeAttendance(int[] records) {
        int left = 0;
        int right = records.length-1;
        while(left < right) {
            int mid = left + (right-left+1)/2;
            if(records[mid] > mid) {
                right = mid -1;
            }else if(records[mid] == mid){
                left = mid;
            }
        }
        return right==records[right]?right+1:right;
    }
}

总结

• 当有 二段性 时,就可以用二分查找,不必有序~

  二段性: 通过某个条件,可以把数组分成两部分,根据题意可以舍弃一部分,这就叫二段性.

模版