912.排序数组
题目:
给你一个整数数组
nums,请你将该数组升序排列。你必须在 不使用任何内置函数 的情况下解决问题,时间复杂度为
O(nlog(n)),并且空间复杂度尽可能小。示例 1:
输入:nums = [5,2,3,1] 输出:[1,2,3,5]示例 2:
输入:nums = [5,1,1,2,0,0] 输出:[0,0,1,1,2,5]提示:
1 <= nums.length <= 5 * 104-5 * 104 <= nums[i] <= 5 * 104
思路:这里就是简单的使用归并排序来解决问题。
想了解归并排序更多细节的小伙伴,可以去看这篇文章:归并排序
代码实现:
class Solution {
public int[] sortArray(int[] nums) {
merge_sort(nums, 0, nums.length-1);
return nums;
}
private void merge_sort(int[] nums, int start, int end) {
// 递归的结束条件:只剩下一个元素
if (start >= end) {
return;
}
// 先分解左子树、再分解右子树
int mid = (start+end) / 2;
merge_sort(nums, start, mid);
merge_sort(nums, mid+1, end);
// 最后将两者合并
merge(nums, start, mid, end);
}
// 合并两个有序数组的操作
private void merge(int[] nums, int start, int mid, int end) {
int s1 = start, e1 = mid, s2 = mid+1, e2 = end;
// 借助辅助数组
int[] array = new int[end-start+1];
int k = 0;
while (s1 <= e1 && s2 <= e2) {
if (nums[s1] < nums[s2]) {
array[k++] = nums[s1++];
} else {
array[k++] = nums[s2++];
}
}
while (s1 <= e1) {
array[k++] = nums[s1++];
}
while (s2 <= e2) {
array[k++] = nums[s2++];
}
// 开始存放到原始数组中
// 从start开始的,总共有K个元素
for (int i = start; i < start+k; i++) { // 也可以直接写为end
nums[i] = array[i-start];
}
}
}LCR170.交易逆序对的总数
题目:
在股票交易中,如果前一天的股价高于后一天的股价,则可以认为存在一个「交易逆序对」。请设计一个程序,输入一段时间内的股票交易记录
record,返回其中存在的「交易逆序对」总数。
示例 1:
输入:record = [9, 7, 5, 4, 6] 输出:8 解释:交易中的逆序对为 (9, 7), (9, 5), (9, 4), (9, 6), (7, 5), (7, 4), (7, 6), (5, 4)。限制:
0 <= record.length <= 50000
思路:这个题目的意思很简单,就是在数组随机找两个数,左边比右边大即可。暴力解法,直接固定左边或者右边的数,再去寻找另外一个数,最终把寻找到的组合数相加即可。
代码实现:
class Solution {
// 暴力枚举
public int reversePairs(int[] record) {
int count = 0;
for (int i = 0; i < record.length; i++) {
for (int j = i+1; j < record.length; j++) {
if (record[i] > record[j]) {
count++;
}
}
}
return count;
}
}很明显,这个方法的时间复杂度为 O(N^2),对于困难题肯定是不会就这么简单的通过的。因此接下来得想办法优化。
最初是在 整个数组中 找 左边 > 右边的组合,但是我们可以将数组划分为两块,左边 找 ,右边 找,最后再一左一右找,这也是符合要求的。 要注意的是,这里找到的组合都得是 前面的数 > 后面的数才行。但是上面的还是没有优化的地方,现在我们再来看一种方法:数组分为两块之后,我们在左边找完组合之后,继续对其进行排序,接着在右边找完组合之后,继续对右边进行排序,最终再找一左一右的组合。上述方法看似排序增加了时间消耗,但是会出现一个非常大的优化效果:排成升序之后,当 左边 数据 大于 右边的数据之后,我们可以下这样一个结论:左边当前位置以后的所有数据都是大于右边的数据的,这就一下子找出了很多数据。
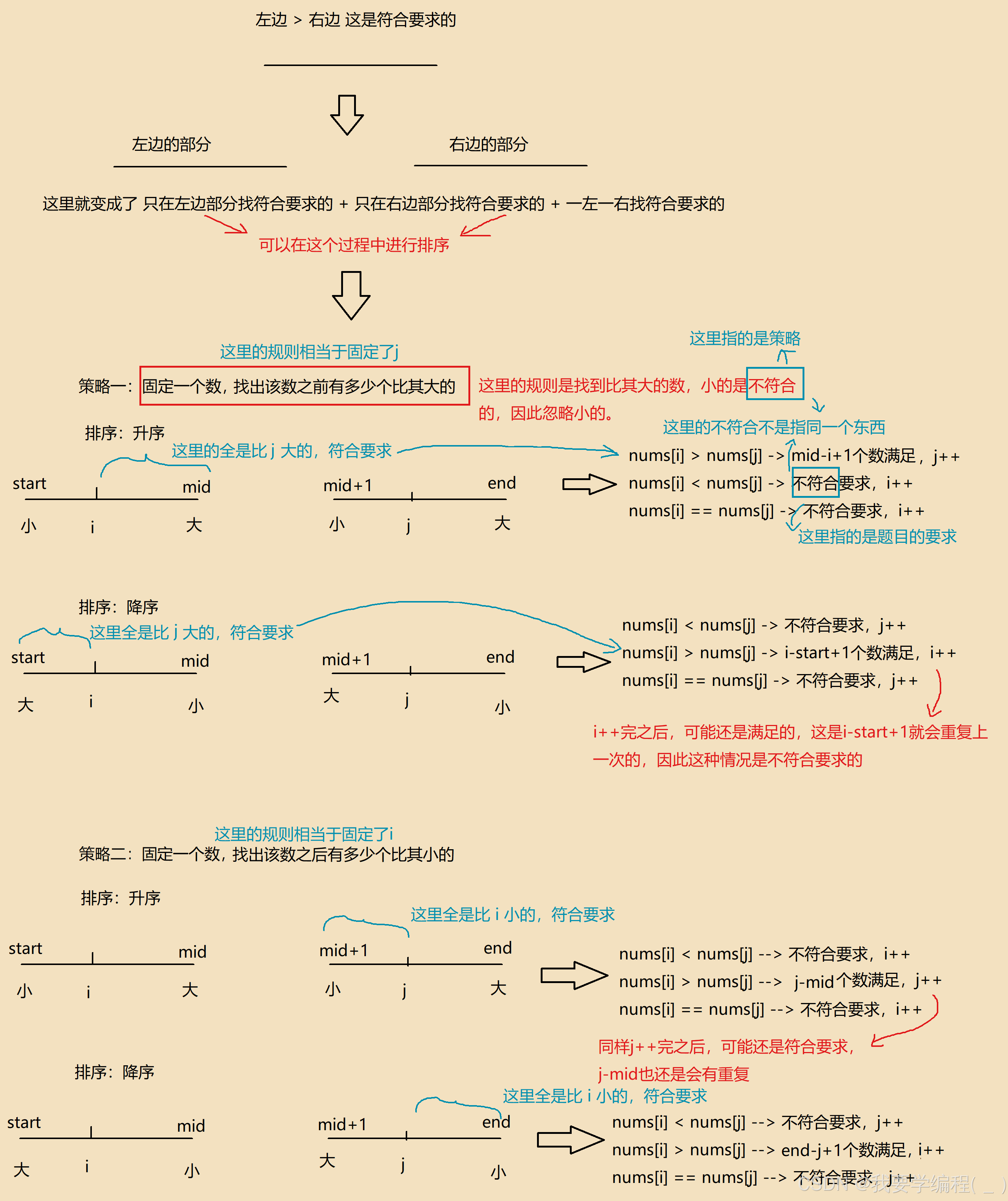
上述过程完全对应着 归并排序。
注意:固定一方之后,只能在另一方找。
代码实现:
升序数组版:
class Solution {
int[] temp; // 避免频繁创建数组,而造成的时间开销
public int reversePairs(int[] record) {
int len = record.length;
temp = new int[len];
// 在归并的过程中就统计
return merge_sort(record, 0, len-1);
}
private int merge_sort(int[] nums, int start, int end) {
if (start >= end) {
return 0; // 不存在逆序对
}
// 递归
int mid = (start + end) / 2;
int ret = 0;
ret += merge_sort(nums, start, mid);
ret += merge_sort(nums, mid+1, end);
// 合并
// 统计
int left = start, right = mid+1, i = 0;
while (left <= mid && right <= end) {
if (nums[left] <= nums[right]) {
temp[i++] = nums[left++];
} else {
ret += (mid-left+1);
temp[i++] = nums[right++];
}
}
while (left <= mid) {
temp[i++] = nums[left++];
}
while (right <= end) {
temp[i++] = nums[right++];
}
// 排序
for (int j = start; j <= end; j++) {
nums[j] = temp[j-start];
}
return ret;
}
}注意:我们这里一定是先统计完当前的数组,再去对当前数组进行排序的。例如,左边数组统计完,右边数组统计完,接着再统计一左一右的情况(这里的数据相对位置还是没有发生变化的),最后再对两者进行排序、
降序数组版:
class Solution {
int[] temp; // 避免频繁创建数组,而造成时间开销
public int reversePairs(int[] record) {
int len = record.length;
temp = new int[len];
return merge_sort(record, 0, len-1);
}
private int merge_sort(int[] nums, int start, int end) {
if (start >= end) {
return 0; // 不存在逆序对
}
int ret = 0;
// 递归
int mid = (start+end) / 2;
ret += merge_sort(nums, start, mid);
ret += merge_sort(nums, mid+1, end);
// 合并
// 统计
int left = start, right = mid+1, i = 0;
while (left <= mid && right <= end) {
if (nums[left] <= nums[right]) {
temp[i++] = nums[right++];
} else {
ret += (end-right+1);
temp[i++] = nums[left++];
}
}
while (left <= mid) {
temp[i++] = nums[left++];
}
while (right <= end) {
temp[i++] = nums[right++];
}
// 排序
for (int j = start; j <= end; j++) {
nums[j] = temp[j-start];
}
return ret;
}
}315.计算右侧小于当前元素的个数
题目:
给你一个整数数组
nums,按要求返回一个新数组counts。数组counts有该性质:counts[i]的值是nums[i]右侧小于nums[i]的元素的数量。
示例 1:
输入:nums = [5,2,6,1] 输出:[2,1,1,0] 解释: 5 的右侧有 2 个更小的元素 (2 和 1) 2 的右侧仅有 1 个更小的元素 (1) 6 的右侧有 1 个更小的元素 (1) 1 的右侧有 0 个更小的元素示例 2:
输入:nums = [-1] 输出:[0]示例 3:
输入:nums = [-1,-1] 输出:[0,0]提示:
1 <= nums.length <= 105-104 <= nums[i] <= 104
思路:这一题与上一题是差不多的,总体上的思路是一致的,只是这里需要返回一个新数组存储的是原数组对应位置大于后面元素的个数即可。因此我们需要采取策略二:固定一个数,找到比当前元素小的数。但由于这里是需要排序的,就会导致元素的下标发生变化,这就需要我们去存储这些下标对应的元素,不过这里不能用哈希的方式,因为这里出现了重复的元素。有一种非常简单的方法:绑定下标与之对应的元素。如果元素发生变化,那么与之对应的下标也随之发生变化即可。因此我们可以申请一个下标数组,到时候如果元素之间交换,下标也要去进行交换。
代码实现:
class Solution {
// 申请 下标数组、最终结果数组、辅助下标数组、辅助数据数组
int[] index;
int[] ret;
int[] temp_index;
int[] temp_nums;
public List<Integer> countSmaller(int[] nums) {
int n = nums.length;
// 初始化数组
index = new int[n];
ret = new int[n];
temp_index = new int[n];
temp_nums = new int[n];
for (int i = 0; i < n; i++) {
// 逻辑上的绑定
index[i] = i;
}
merge(nums, 0, n-1);
List<Integer> list = new ArrayList<>();
for (int i = 0; i < n; i++) {
list.add(ret[i]);
}
return list;
}
private void merge(int[] nums, int start, int end) {
// 1、防止越界
if (start >= end) {
return;
}
// 2、处理左侧数据、处理右侧数据
int mid = (start+end) / 2;
merge(nums, start, mid);
merge(nums, mid+1, end);
// 3、处理一左一右的情况
int left = start, right = mid+1, i = 0;
while (left <= mid && right <= end) { // 进行降序排序
if (nums[left] <= nums[right]) { // 不符合要求,直接排序即可
// 既要把基本的数据排序,也要对绑定的下标排序
temp_nums[i] = nums[right];
temp_index[i++] = index[right++];
} else {
// 统计对应下标的数据(这里一定得是原始下标)
ret[index[left]] += (end-right+1);
// 继续进行排序
temp_nums[i] = nums[left];
temp_index[i++] = index[left++];
}
}
while (left <= mid) {
temp_nums[i] = nums[left];
temp_index[i++] = index[left++];
}
while (right <= end) {
temp_nums[i] = nums[right];
temp_index[i++] = index[right++];
}
// 4、处理剩下的排序
for (int j = start; j <= end; j++) {
// 基本数据 + 下标
nums[j] = temp_nums[j-start];
index[j] = temp_index[j-start];
}
}
}注意:策略二,我们采取的是降序排序。
493. 翻转对
题目:
给定一个数组
nums,如果i < j且nums[i] > 2*nums[j]我们就将(i, j)称作一个重要翻转对。你需要返回给定数组中的重要翻转对的数量。
示例 1:
输入: [1,3,2,3,1] 输出: 2示例 2:
输入: [2,4,3,5,1] 输出: 3注意:
- 给定数组的长度不会超过
50000。- 输入数组中的所有数字都在32位整数的表示范围内。
思路:本题与前面两题差不多的思路,但稍微有点不同,这里我们不再是统计 nums[i] > nums[j] 了,而是统计 nums[i] > 2*nums[j] ,这里就需要注意了,不能再将 统计的代码 与 归并排序的代码混在一起了,前面我们之所以将两者混在一起是因为统计的判断逻辑与归并排序的判断逻辑相同,因此这里得先去统计,然后再去排序。
代码实现:
数组升序版:
class Solution {
int[] temp; // 申请辅助数组
public int reversePairs(int[] nums) {
int n = nums.length;
temp = new int[n];
return merge(nums, 0, n-1);
}
private int merge(int[] nums, int start, int end) {
// 处理不符合要求的
if (start >= end) {
return 0;
}
// 处理左边、右边
int ret = 0;
int mid = (start+end) / 2;
ret += merge(nums, start, mid);
ret += merge(nums, mid+1, end);
// 处理一左一右的情况
int left = start, right = mid+1, i = 0;
while (left <= mid && right <= end) { // 只有两个区间都有值时,才去计算
// 这里得去处理数据溢出的问题
if ((long)(nums[left]) <= 2*(long)nums[right]) { // 不符合要求的
left++;
} else { // 符合要求的
ret += mid-left+1;
right++;
}
}
// 进行归并排序
left = start;
right = mid+1;
while (left <= mid && right <= end) { // 采取升序排序
if (nums[left] <= nums[right]) {
temp[i++] = nums[left++];
} else {
temp[i++] = nums[right++];
}
}
while (left <= mid) {
temp[i++] = nums[left++];
}
while (right <= end) {
temp[i++] = nums[right++];
}
// 处理最后的排序问题
for (int j = start; j <= end; j++) {
nums[j] = temp[j-start];
}
return ret;
}
}数组降序版:
class Solution {
int[] temp; // 申请辅助数组
public int reversePairs(int[] nums) {
int n = nums.length;
temp = new int[n];
return merge(nums, 0, n-1);
}
private int merge(int[] nums, int start, int end) {
// 处理不符合要求的
if (start >= end) {
return 0;
}
// 处理左边、右边
int ret = 0;
int mid = (start+end) / 2;
ret += merge(nums, start, mid);
ret += merge(nums, mid+1, end);
// 处理一左一右的情况
int left = start, right = mid+1, i = 0;
while (left <= mid && right <= end) { // 只有两个区间都有值时,才去计算
// 这里得去处理数据溢出的问题
if ((long)(nums[left]) <= 2*(long)nums[right]) { // 不符合要求的
right++;
} else { // 符合要求的
ret += end-right+1;
left++;
}
}
// 进行归并排序
left = start;
right = mid+1;
while (left <= mid && right <= end) { // 采取降序排序
if (nums[left] <= nums[right]) {
temp[i++] = nums[right++];
} else {
temp[i++] = nums[left++];
}
}
while (left <= mid) {
temp[i++] = nums[left++];
}
while (right <= end) {
temp[i++] = nums[right++];
}
// 处理最后的排序问题
for (int j = start; j <= end; j++) {
nums[j] = temp[j-start];
}
return ret;
}
}好啦!本期 一文详解“分治—归并“在算法中的应用 的学习之旅 就到此结束啦!

