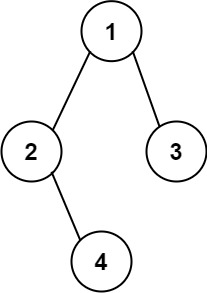
二叉树的前序遍历
题目:
给你二叉树的根节点
root,返回它节点值的 前序 遍历。
示例 1:
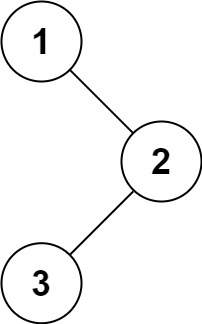
输入:root = [1,null,2,3] 输出:[1,2,3]示例 2:
输入:root = [] 输出:[]示例 3:
输入:root = [1] 输出:[1]示例 4:
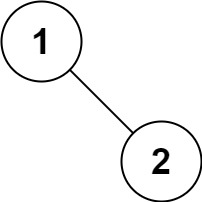
输入:root = [1,2] 输出:[1,2]示例 5:
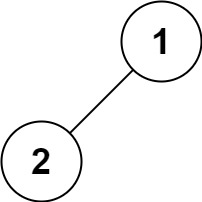
输入:root = [1,null,2] 输出:[1,2]提示:
- 树中节点数目在范围
[0, 100]内-100 <= Node.val <= 100
这个题目如果用递归去做那就比较简单了,但是现在我们要采用非递归的方法来写。
思路:利用栈,将遍历到的所有根结点都入栈(以前序遍历的路线去走) ,并且将这些节点都放入List当中。当遇到 null 时,就开始出栈顶的元素,并且以栈顶元素的 right 指针来重新遍历这棵树,直至栈为空即可。
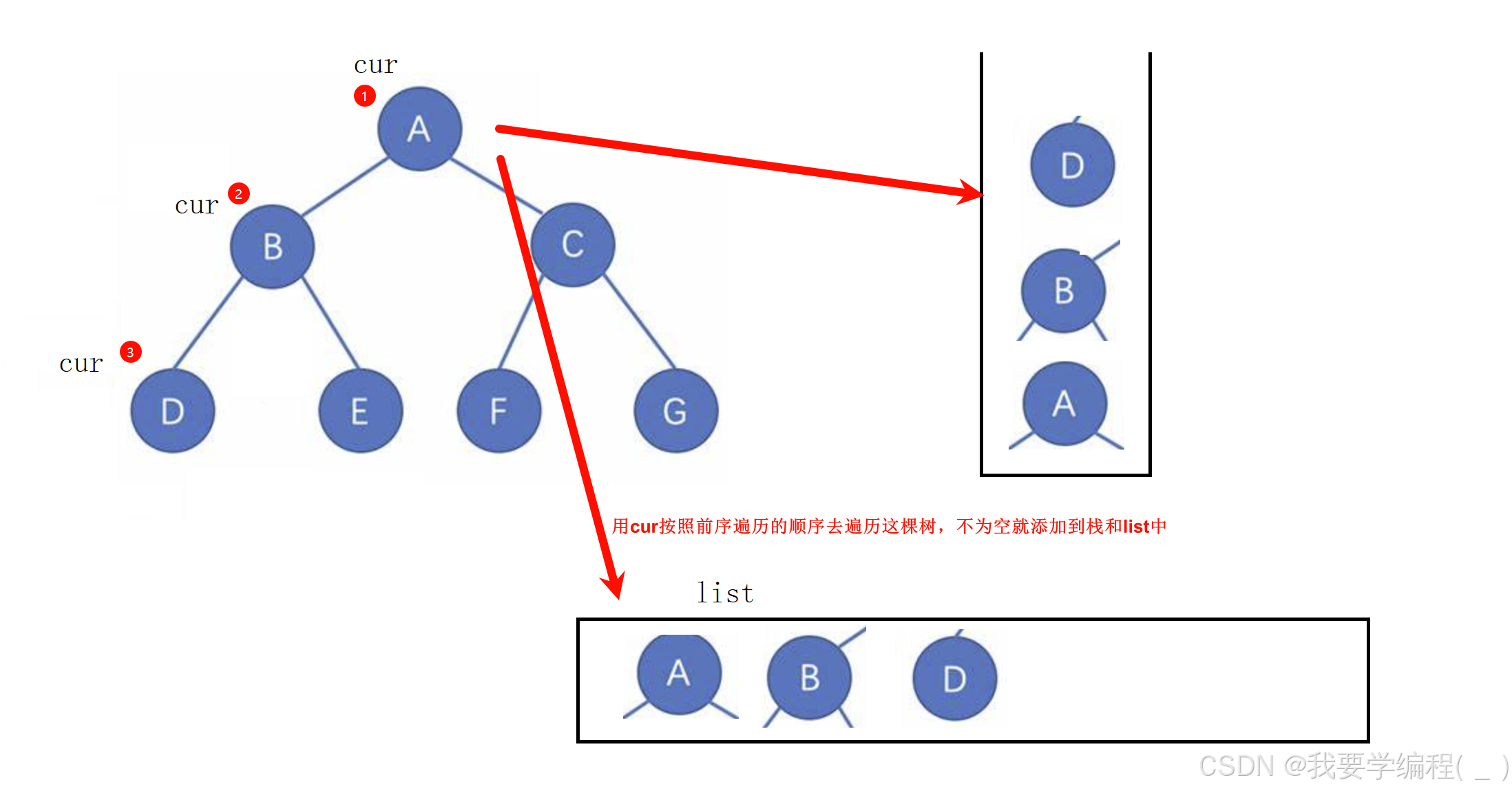
代码实现:
class Solution {
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> list = new LinkedList<>();
if (root == null) {
return list;
}
Stack<TreeNode> stack = new Stack<>();
TreeNode cur = root;
// 因为第一次时,这个循环进不来,所以就加了 cur != null 这个条件
while (cur != null || !stack.isEmpty()) {
while (cur != null) {
// 根结点
stack.push(cur);
list.add(cur.val);
// 左子树
cur = cur.left;
}
TreeNode top = stack.pop();
// 右子树
cur = top.right;
}
return list;
}
}既然前序遍历的代码出来了,那么中序遍历和后序遍历也就可以搞定了。
中序遍历:
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> list = new LinkedList<>();
if (root == null) {
return list;
}
Stack<TreeNode> stack = new Stack<>();
TreeNode cur = root;
while (cur != null || !stack.isEmpty()) {
while (cur != null) {
// 左子树
stack.push(cur);
cur = cur.left;
}
TreeNode top = stack.pop();
// 根结点
list.add(top.val);
// 右子树
cur = top.right;
}
return list;
}
}后序遍历:
class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> list = new LinkedList<>();
if (root == null) {
return list;
}
Stack<TreeNode> stack = new Stack<>();
TreeNode cur = root;
TreeNode prev = null; // 记录添加的前一个位置(防止死循环)
while (cur != null || !stack.isEmpty()) {
while (cur != null) {
stack.push(cur);
cur = cur.left;
}
// 注意这里不能是pop,因为我们不能确定这个节点的右边是否还有节点
TreeNode top = stack.peek();
// 如果右边还有元素,那就得去遍历它;否则,就打印(左为null,右也为null)
if (top.right == null || top.right == prev) { // 右边被处理过才能进来
list.add(top.val);
prev = stack.pop(); // 更新为前一个位置的值
} else {
cur = top.right;
}
}
return list;
}
}总结:其实只要我们知道遍历的顺序,从遍历顺序去解决,那么这种题目就迎刃而解了。
二叉树的层序遍历
题目:
给你二叉树的根节点
root,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。
示例 1:
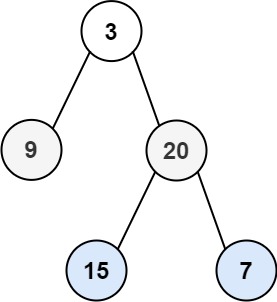
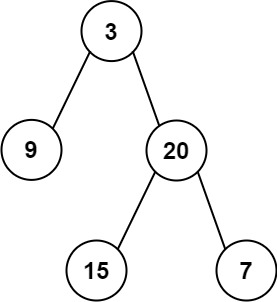
输入:root = [3,9,20,null,null,15,7] 输出:[[3],[9,20],[15,7]]示例 2:
输入:root = [1] 输出:[[1]]示例 3:
输入:root = [] 输出:[]提示:
- 树中节点数目在范围
[0, 2000]内-1000 <= Node.val <= 1000
思路:通过队列来存储树中的节点,先储存根结点,再把根结点出队,判断左右子树是否为空,来使其入队。
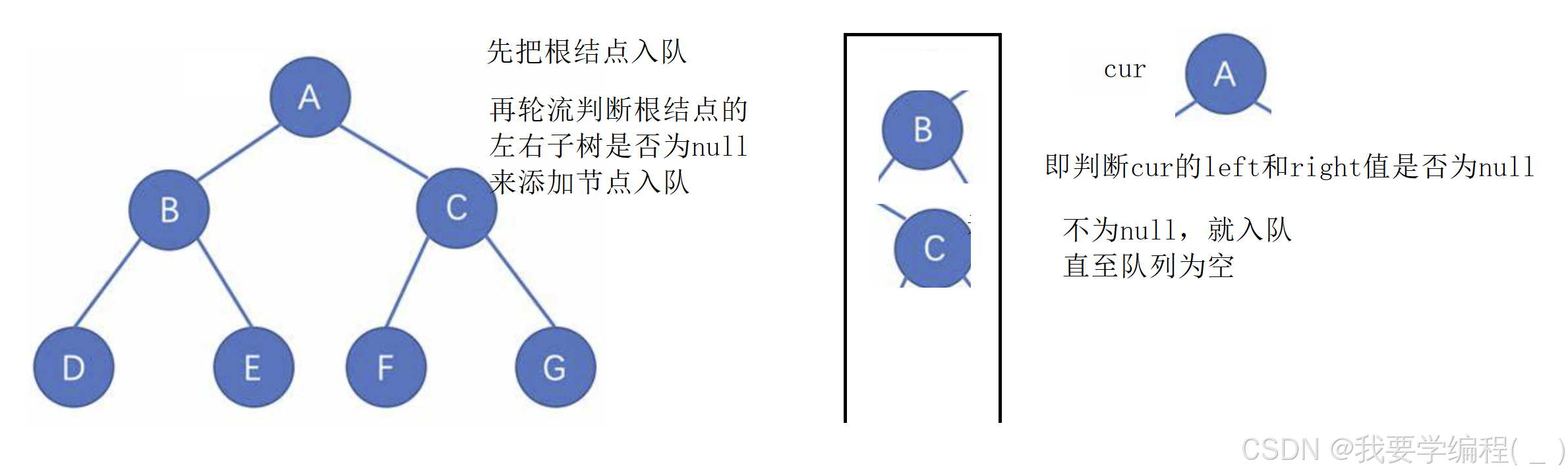
代码实现:
class Solution {
public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> ret = new LinkedList<>();
// 通过队列进行层序遍历
if (root == null) {
return ret;
}
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()) {
List<Integer> list = new LinkedList<>();
// 记录每一层的个数
int size = queue.size();
// 先把每一层的节点都放到list中
while (size-- > 0) {
TreeNode cur = queue.poll();
list.add(cur.val);
if (cur.left != null) {
queue.offer(cur.left);
}
if (cur.right != null) {
queue.offer(cur.right);
}
}
// 再把每一层的list放到总的ret中
ret.add(list);
}
return ret;
}
}刚刚我们是从上往下遍历这棵树的,现在如果让我们从下往上遍历这棵树呢?
二叉树的层序遍历 II
题目:
给你二叉树的根节点
root,返回其节点值 自底向上的层序遍历 。 (即按从叶子节点所在层到根节点所在的层,逐层从左向右遍历)
示例 1:
输入:root = [3,9,20,null,null,15,7] 输出:[[15,7],[9,20],[3]]示例 2:
输入:root = [1] 输出:[[1]]示例 3:
输入:root = [] 输出:[]提示:
- 树中节点数目在范围
[0, 2000]内-1000 <= Node.val <= 1000
思路:从上往下我们已经知道了该怎么遍历,但是从下往上不知道该从何下手?这是我们就可以采用换汤不换药的方法了。即将从上到下的遍历结果储存起来,然后再交换两者的值即可。这样我们最终得到的值就是从下往上遍历的结果了。
代码实现:
class Solution {
public List<List<Integer>> levelOrderBottom(TreeNode root) {
List<List<Integer>> ret = new LinkedList<>();
if (root == null) {
return ret;
}
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()) {
List<Integer> list = new LinkedList<>();
int size = queue.size();
while (size-- > 0) {
TreeNode cur = queue.poll();
list.add(cur.val);
if (cur.left != null) {
queue.offer(cur.left);
}
if (cur.right != null) {
queue.offer(cur.right);
}
}
ret.add(list);
}
// 现在ret中是按照从上往下的顺序存储的,我们需要的刚好相反,即需要交换
swap(ret);
return ret;
}
private void swap(List<List<Integer>> ret) {
int left = 0;
int right = ret.size()-1;
while (left < right) {
// 交换
List<Integer> tmp = ret.get(left);
ret.set(left, ret.get(right));
ret.set(right, tmp);
left++;
right--;
}
}
}还有一种实现方式:就是在插入时,我们不采用尾插的方式,采用头插的方式去构建LIst。
// 采用头插的方式
ret.addFirst(list);前序遍历、中序遍历、后续遍历的迭代版实现和层序遍历的实现所用的数据结构不同的原因:
不管是前序遍历、中序遍历还是后序遍历,都是左子树的遍历顺序在前,右子树的遍历顺序在后,这就导致了一个问题:如果根结点找不到了(先打印了,就出队列了),那么怎么去找右子树呢?因此我们的需求就是把二叉树的根结点存储起来,即让其最后再出去。这个的效果就是先进后出——> 栈 ;而层序遍历就没有这样的需求了,即从上往下、从左往右依次遍历打印,那么我们打印完这一层的节点之后,就可以舍弃它们了。即先进先出——>队列。
前面我们学习了给了前序和中序遍历或者后续和中序遍历,来构建二叉树,现在我们就用代码来实现一下:
从前序与中序遍历序列构造二叉树
题目:
给定两个整数数组
preorder和inorder,其中preorder是二叉树的先序遍历,inorder是同一棵树的中序遍历,请构造二叉树并返回其根节点。
示例 1:
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7] 输出: [3,9,20,null,null,15,7]示例 2:
输入: preorder = [-1], inorder = [-1] 输出: [-1]提示:
1 <= preorder.length <= 3000inorder.length == preorder.length-3000 <= preorder[i], inorder[i] <= 3000preorder和inorder均 无重复 元素inorder均出现在preorderpreorder保证 为二叉树的前序遍历序列inorder保证 为二叉树的中序遍历序列
思路:与我们做选填是一样的。通过前序遍历来确定二叉树的根结点,再通过根结点在中序遍历中的位置来确定左子树和右子树,而前序遍历往后,就是左子树的根结点,再确定在中序遍历中的位置来确定左子树的根结点的左子树和右子树。一直这样递归下去,直至左子树的下标大于右子树的下标(在中序遍历中) 。

代码实现:
class Solution {
// 创建一棵二叉树,先创建根结点,再创建左子树和右子树
// 根结点就是根据前序遍历来找,
// 左子树和右子树都是根据前序遍历和中序遍历来找出左子树和右子树的根结点
private int rootIndex;
public TreeNode buildTree(int[] preorder, int[] inorder) {
return buildTreeChild(preorder, inorder, 0, inorder.length-1);
}
private TreeNode buildTreeChild(int[] preorder, int[] inorder,
int inorderbegin, int inorderend) {
// 空树
if (inorderbegin > inorderend) {
return null;
}
// 创建根结点
TreeNode root = new TreeNode(preorder[rootIndex]);
// 找到边界
int border = findVal(inorder, preorder[rootIndex]);
rootIndex++;
// 创建左子树
root.left = buildTreeChild(preorder, inorder, inorderbegin, border-1);
// 创建右子树
root.right = buildTreeChild(preorder, inorder, border+1, inorderend);
return root;
}
// 找到根结点在中序遍历中的位置来划分左子树和右子树
private int findVal(int[] inorder, int val) {
for (int i = 0; i < inorder.length; i++) {
if (inorder[i] == val) {
return i;
}
}
return -1;
}
}前序学完了,还有后序:
从中序与后序遍历序列构造二叉树
思路:后序遍历同样是确定根结点的位置,从后序遍历数组的末尾开始遍历根节点,在中序遍历中寻找到根结点的位置并划分左右子树。与上述思路类似。
注意:后序遍历是:左子树 右子树 根;而前序遍历是:根 左子树 右子树 。这也就意味着前序遍历找到的根是左子树的根(除祖先节点外) ,即我们先得创建左子树;而后序遍历找到的根是右子树的根(除祖先节点外),即我们先得创建右子树。因为创建二叉树其实就是依赖于根结点,谁于根结点临近创建谁。
class Solution {
// 后续遍历找到根结点,再根据根结点确定左子树和右子树
private int rootIndex;
public TreeNode buildTree(int[] inorder, int[] postorder) {
rootIndex = postorder.length-1;
return buildTreeChild(inorder, postorder, 0, inorder.length-1);
}
private TreeNode buildTreeChild(int[] inorder, int[] postorder,
int inorderbegin, int inorderend) {
if (inorderbegin > inorderend) {
return null;
}
TreeNode root = new TreeNode(postorder[rootIndex]);
// 在中序遍历的数组中找到根结点的位置
int border = findVal(inorder, postorder[rootIndex]);
rootIndex--;
root.right = buildTreeChild(inorder, postorder, border+1, inorderend);
root.left = buildTreeChild(inorder, postorder, inorderbegin, border-1);
return root;
}
private int findVal(int[] inorder, int val) {
for (int i = 0; i < inorder.length; i++) {
if (inorder[i] == val) {
return i;
}
}
return -1;
}
}二叉树的最近公共祖先
题目:
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
示例 1:
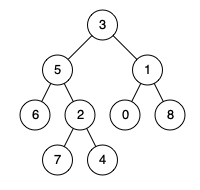
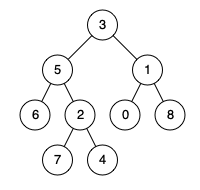
输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1 输出:3 解释:节点5和节点1的最近公共祖先是节点3 。示例 2:
输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4 输出:5 解释:节点5和节点4的最近公共祖先是节点5 。因为根据定义最近公共祖先节点可以为节点本身。示例 3:
输入:root = [1,2], p = 1, q = 2 输出:1提示:
- 树中节点数目在范围
[2, 105]内。-109 <= Node.val <= 109- 所有
Node.val互不相同。p != qp和q均存在于给定的二叉树中。
思路一:采用穷举的方法,看看会出现几种情况。
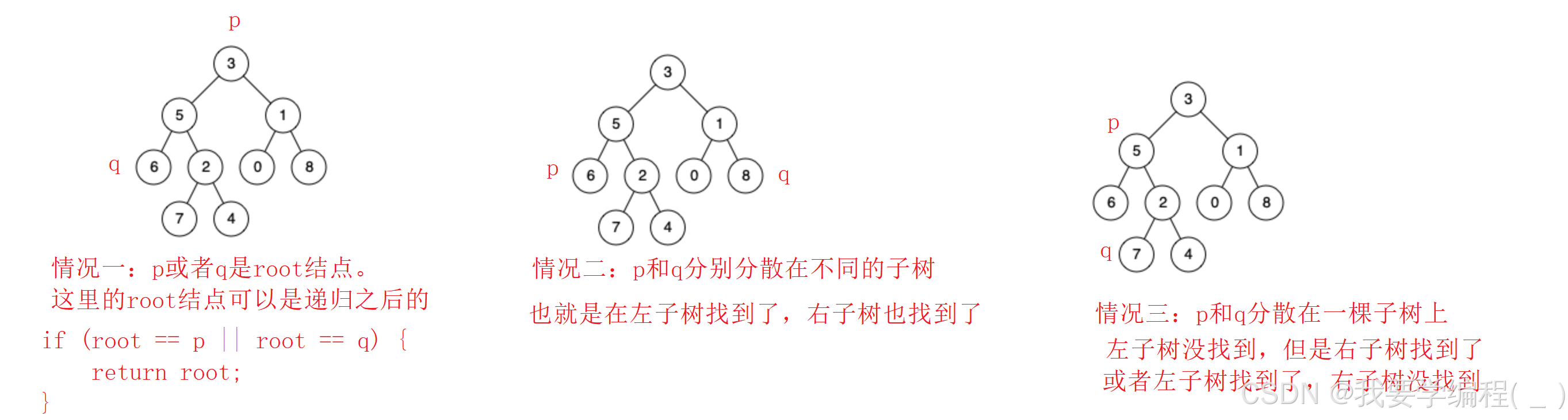
上面三种情况其实就是通过示例总结出来的
代码实现:
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
// 在递归去寻找的过程中可能会出现下面两种情况(限制条件)
if (root == null) {
return null;
}
if (root == q || root == p) {
return root;
}
// 走到这里说明根结点一定不存在,则判断左子树和右子树即可
// 遍历左子树
TreeNode leftTree = lowestCommonAncestor(root.left, p, q);
// 遍历右子树
TreeNode rightTree = lowestCommonAncestor(root.right, p, q);
// 再遍历完成之后,我们就来判断是哪种情况
if (leftTree != null && rightTree != null) {
return root;
}
if (leftTree != null && rightTree == null) {
return leftTree;
}
// 下面的代码可以简化为 return rightTree;
if (leftTree == null && rightTree != null) {
return rightTree;
}
return null;
}
}如果我们总结不出来,也没关系。还有另外一种方法,就是把p和q出现的路线储存起来,然后再去一 一比较,遇到第一个相等的就是公共的祖先。
首先,得确定是用什么数据结构来储存路线。栈 还是 队列呢?其实都是可以的。因为我们采用的是从上往下遍历,那么根结点一定是最先被放入栈(队列)中的。而我们比较的方式不同,就导致了储存的方式不同。如果我们是想找不同,那就得用队列,从根结点开始比较;如果我们是想找相同,那就得用栈,从p和q开始比较,找到相同的节点。
栈的实现方式:
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
Stack<TreeNode> stackP = new Stack<>();
Stack<TreeNode> stackQ = new Stack<>();
getPath(root, p, stackP);
getPath(root, q, stackQ);
// 先让长的走差值步数
if (stackP.size() > stackQ.size()) {
int size = stackP.size() - stackQ.size();
while (size-- > 0) {
stackP.pop();
}
} else {
int size = stackQ.size() - stackP.size();
while (size-- > 0) {
stackQ.pop();
}
}
// 开始一起出
while (stackQ.peek() != stackP.peek()) {
stackQ.pop();
stackP.pop();
}
return stackQ.peek();
}
private TreeNode getPath(TreeNode root, TreeNode target, Stack<TreeNode> stack) {
if (root == null) {
return null;
}
stack.push(root); // 先得把这个入栈
if (root == target) {
return root;
}
// 左子树
TreeNode leftTree = getPath(root.left, target, stack);
if (leftTree != null) { // 左子树不为null,说明在左子树找到了,即返回
return leftTree;
}
// 右子树
TreeNode rightTree = getPath(root.right, target, stack);
if (rightTree != null) { // 右子树不为null,说明在右子树找到了,即返回
return rightTree;
}
// 左右子树的遍历结果都是null,即都没找到,就出栈
if (leftTree == null && rightTree == null) {
stack.pop();
}
return null;
}
}在用队列去写时,我们就会发现一个问题:如果左右子树都为null,那么证明这个节点不是我们路径上的节点,就得出队,但是队列的数据是先进先出的特点,不满足我们的要求,即普通队列是不行的。因此,就只能用栈。
我们在分析问题时,可能刚刚不会遇到这点,但是后面在做题时,体会到了这点就行,不管是什么思路,我们都得上手去写才可以。
根据二叉树创建字符串
题目:
给你二叉树的根节点
root,请你采用前序遍历的方式,将二叉树转化为一个由括号和整数组成的字符串,返回构造出的字符串。空节点使用一对空括号对
"()"表示,转化后需要省略所有不影响字符串与原始二叉树之间的一对一映射关系的空括号对。
示例 1:
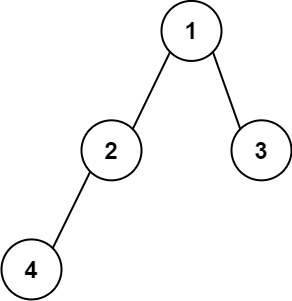
输入:root = [1,2,3,4] 输出:"1(2(4))(3)" 解释:初步转化后得到 "1(2(4)())(3()())" ,但省略所有不必要的空括号对后,字符串应该是"1(2(4))(3)" 。示例 2:
输入:root = [1,2,3,null,4] 输出:"1(2()(4))(3)" 解释:和第一个示例类似,但是无法省略第一个空括号对,否则会破坏输入与输出一一映射的关系。提示:
- 树中节点的数目范围是
[1, 104]-1000 <= Node.val <= 1000
思路:根据示例,我们就可以看出:遇到左子树就得添加“(”,当左子树走完,就得添加“)”,当左子树为null,并且右子树不为null时,得添加“()”。
代码实现:
class Solution {
// 通过 StringBuild 来构建字符串
private StringBuilder sb = new StringBuilder();
public String tree2str(TreeNode root) {
dfs(root);
return sb.toString();
}
private void dfs(TreeNode root) {
if (root == null) {
return;
}
// 根结点
sb.append(root.val);
// 根的左子树
if (root.left != null) {
sb.append("(");
// 继续递归去左子树寻找
dfs(root.left);
// 左子树走完了得加右括号
sb.append(")");
} else {
if (root.right != null) {
// 左边添加一对空括号
sb.append("()");
} else {
return;
}
}
// 根的右子树
if (root.right != null) {
sb.append("(");
dfs(root.right);
sb.append(")");
} else {
return;
}
}
}总结:通过上面几题的练习,我们不难发现其实有的题目需要我们去利用示例的规律来写,但更多的题目是需要我们对数据结构进行不断的学习和熟练,这样才能更加得心应手。
好啦!本期 数据结构之初始二叉树(4)的学习之旅就到此结束啦!二叉树的折磨也是暂时的结束啦!即将开启新的数据结构之旅!我们下一期再一起学习吧!