100. 相同的树
题目:
给你两棵二叉树的根节点
p和q,编写一个函数来检验这两棵树是否相同。如果两个树在结构上相同,并且节点具有相同的值,则认为它们是相同的。
示例 1:
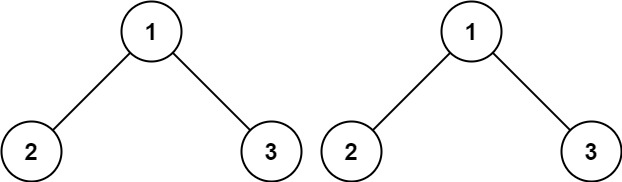
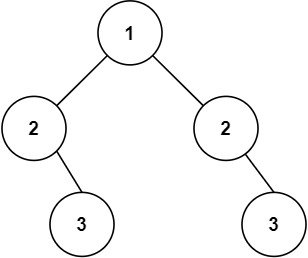
输入:p = [1,2,3], q = [1,2,3] 输出:true示例 2:
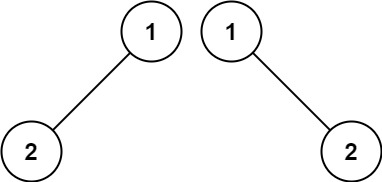
输入:p = [1,2], q = [1,null,2] 输出:false示例 3:
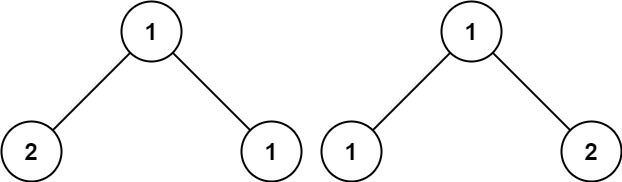
输入:p = [1,2,1], q = [1,1,2] 输出:false提示:
- 两棵树上的节点数目都在范围
[0, 100]内-104 <= Node.val <= 104
思路: 按照上面的套路,我们应该找到一个节点所做的事情,即判断这个节点是否相同。
if (p.val != q.val) {
return false;
}上面这个代码的确是我们判读判断的逻辑,但是还要注意 p 和 q 可能出现为 null 的情况。因此还要排除,并且当两者同时为 null 时,我们要返回 true。因为空树也是相同的树。
// 一个是空树,一个不是,不符合
if (p == null && q != null || p != null && q == null) {
return false;
}
// 两个都是空树,符合
if (p == null && q == null) {
return true;
}
一个节点的事情处理完了,就该开始套框架,递归了。我们先不看框架,这个方法处理的是一个节点的(可以理解为根结点),接下来就要开始处理左子树和右子树。也就是递归处理。
// 判断左子树 判断右子树
return isSameTree(p.left, q.left) && isSameTree(p.right, q.right);只有当左右子树和根都为true时,才能返回true。
思路整理完成就可以实现全部的代码了。
代码实现:
class Solution {
public boolean isSameTree(TreeNode p, TreeNode q) {
// 根结点的判断
if (p == null && q != null || p != null && q == null) {
return false;
}
if (p == null && q == null) {
return true;
}
if (p.val != q.val) {
return false;
}
// 左右子树的判断
return isSameTree(p.left, q.left) && isSameTree(p.right, q.right);
}
}注意:如果我们是在不放心这个方法,那么写完之后,就可以检查这个方法内容是否满足递归的两个条件:1、存在限制条件;2、每次递归之后都将进一步接近这个条件。
限制条件:就是什么时候,这个递归将会停止。很明显,当遇到空树时,就可以停止了,因为空树没有左右子树了。我们上面的代码满足这个条件,遇到空树就会返回。
随着递归的深入,我们会很明显的发现越来越接近限制条件。
怎么样?是不是觉得这个方法非常的好用?是不是觉得自己现在强的可怕?别担心,下面还有很多硬菜等着我们去品尝,慢慢来吧。
572. 另一棵树的子树
题目:
给你两棵二叉树
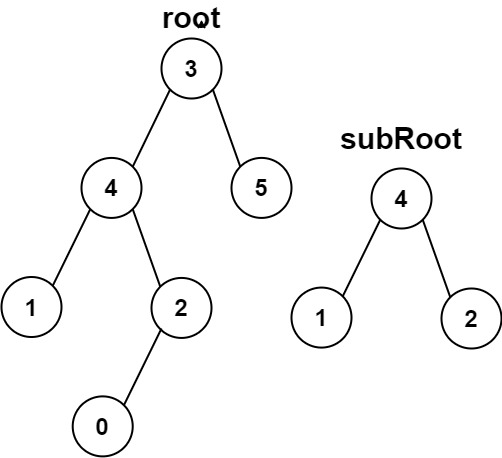
root和subRoot。检验root中是否包含和subRoot具有相同结构和节点值的子树。如果存在,返回true;否则,返回false。二叉树
tree的一棵子树包括tree的某个节点和这个节点的所有后代节点。tree也可以看做它自身的一棵子树。
示例 1:
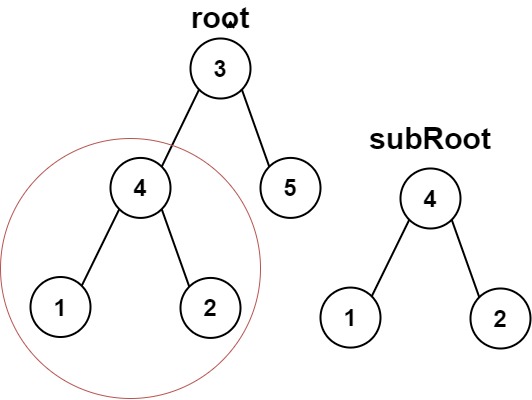
输入:root = [3,4,5,1,2], subRoot = [4,1,2] 输出:true示例 2:
输入:root = [3,4,5,1,2,null,null,null,null,0], subRoot = [4,1,2] 输出:false提示:
root树上的节点数量范围是[1, 2000]subRoot树上的节点数量范围是[1, 1000]-104 <= root.val <= 104-104 <= subRoot.val <= 104
思路:判断一棵树是否为另一棵树的子树,换句话说,就是看一棵树中是否有子树和另一棵树相同。可以理解为上一题的变形版。同样,先明确根结点要做的事情,判断根结点所在的树是否与另一颗相同,另外就是套框架,递归根结点的左子树、右子树,看是否与另一个子树相同
根结点做的事情:
// 根结点为空,直接不需要比较了,这个也是限制条件
if (root == null) {
return false;
}
// 判断根结点所在的子树是否另一棵子树相同
if (isSameTree(root, subRoot)) {
return true;
}框架:
// 左子树相同了,就不需要比较了
if (isSubtree(root.left, subRoot)) {
return true;
}
// 不管右子树的比较结果如何,都可以直接返回了
return isSubtree(root.right, subRoot);代码实现:
class Solution {
public boolean isSubtree(TreeNode root, TreeNode subRoot) {
// 判断是否存在root的子树和subRoot是相同的树
// 限制条件:什么时候可以停止递归了?root为null了,找不到了
if (root == null) {
return false;
}
// 先判断根结点
if (isSameTree(root, subRoot)) {
return true;
}
// 递归判断左子树
if (isSubtree(root.left, subRoot)) {
return true;
}
// 递归判断右子树
return isSubtree(root.right, subRoot);
}
// 判断这两颗树是否相同
private boolean isSameTree(TreeNode root, TreeNode subRoot) {
// 根 左子树 右子树
if (root == null && subRoot != null || root != null && subRoot == null) {
return false;
}
if (root == null && subRoot == null) {
return true;
}
if (subRoot.val != root.val) {
return false;
}
// 递归判断左子树 && 递归判断右子树
return isSameTree(root.left, subRoot.left) && isSameTree(root.right, subRoot.right);
}
}226. 翻转二叉树
题目:
给你一棵二叉树的根节点
root,翻转这棵二叉树,并返回其根节点。
示例 1:
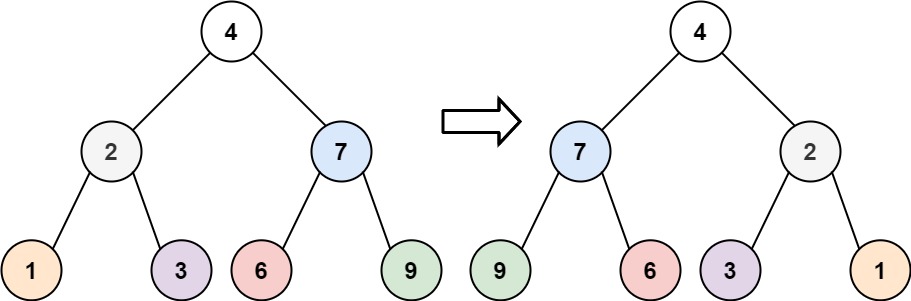
输入:root = [4,2,7,1,3,6,9] 输出:[4,7,2,9,6,3,1]示例 2:
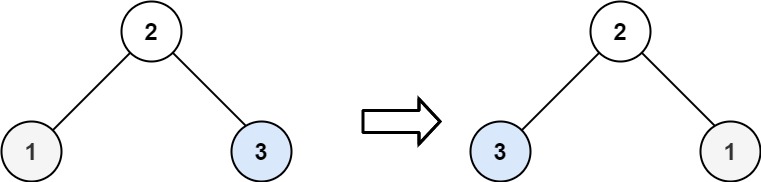
输入:root = [2,1,3] 输出:[2,3,1]示例 3:
输入:root = [] 输出:[]提示:
- 树中节点数目范围在
[0, 100]内-100 <= Node.val <= 100
思路一:翻转二叉树就是将每个结点的左子树和右子树都进行交换。
根结点做的事情:
交换根的左子树和根的右子树。
// 空节点不需要交换
if (root == null) {
return root;
}
// 交换
TreeNode tmp = root.left;
root.left = root.right;
root.right = tmp;框架:
// 根的左子树 和 根的右子树
invertTree(root.left);
invertTree(root.right);代码实现:
class Solution {
public TreeNode invertTree(TreeNode root) {
if (root == null) {
return root;
}
// 先翻转根结点
TreeNode tmp = root.left;
root.left = root.right;
root.right = tmp;
// 翻转左子树
invertTree(root.left);
// 翻转右子树
invertTree(root.right);
return root;
}
}其实,如果我们仔细观察会发现,叶子结点是不需要交换的,因为叶子结点的左子树和右子树都是空,交换前后不变。
if (root.left == null && root.right == null) {
return root;
}注意:虽然我们的限制条件改成了叶子结点,但是root 判空的语句还是得有,因为测试用例的root可能为null。
思路二:上面的思路是从根结点开始进行交换,但是进行左右子树交换时,并没有用到其返回值,因此,这个思路就是先从根的左子树和右子树开始交换,交换的结果储存起来,再去交换根的左右子树。
根结点做的事情:
if (root == null) {
return root;
}
// 叶子结点直接返回即可
if (root.left == null && root.right == null) {
return root;
}
// 根的左子树和右子树进行了递归翻转
.......
// 开始交换本级根的左子树和右子树
root.left = rightTree;
root.right = leftTree;框架:
// 翻转左子树的结果
TreeNode leftTree = invertTree(root.left);
// 翻转右子树的结果
TreeNode rightTree = invertTree(root.right);代码实现:
class Solution {
public TreeNode invertTree(TreeNode root) {
if (root == null) {
return root;
}
// 叶子结点直接返回即可
if (root.left == null && root.right == null) {
return root;
}
// 翻转左子树的结果
TreeNode leftTree = invertTree(root.left);
// 翻转右子树的结果
TreeNode rightTree = invertTree(root.right);
// 开始交换本级根的左子树和右子树
root.left = rightTree;
root.right = leftTree;
return root;
}
}101. 对称二叉树
题目:
给你一个二叉树的根节点
root, 检查它是否轴对称。
示例 1:
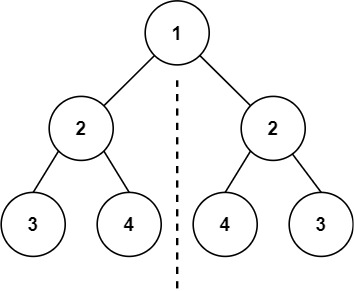
输入:root = [1,2,2,3,4,4,3] 输出:true示例 2:
输入:root = [1,2,2,null,3,null,3] 输出:false提示:
- 树中节点数目在范围
[1, 1000]内-100 <= Node.val <= 100
思路:判断是否为对称二叉树其实就是看这个根结点的左右子树是否可以翻转。那么这个题目就变成了判断根的左右子树是可以翻转
public boolean isSymmetric(TreeNode root) {
// 比较根结点的左子树和右子树
return invertTree(root.left, root.right);
}根结点做的事情:(节点是否相同)
if (left == null && right != null || left != null && right == null) {
return false;
}
if (left == null && right == null) {
return true;
}
if (left.val != right.val) {
return false;
}框架:
// 最外围是否可以翻转 、 内围是否可以翻转
return invertTree(left.left, right.right) && invertTree(left.right, right.left);代码实现:
class Solution {
public boolean isSymmetric(TreeNode root) {
// 比较根结点的左子树和右子树
return invertTree(root.left, root.right);
}
// 就是比较对应结点的值是否一样
public boolean invertTree(TreeNode left, TreeNode right) {
if (left != null && right == null || left == null && right != null) {
return false;
}
if (left == null && right == null) {
return true;
}
if (left.val != right.val) {
return false;
}
return invertTree(left.left, right.right) && invertTree(left.right, right.left);
}
}110. 平衡二叉树
给定一个二叉树,判断它是否是 平衡二叉树
示例 1:
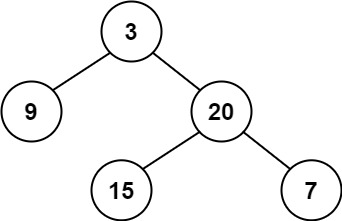
输入:root = [3,9,20,null,null,15,7] 输出:true示例 2:
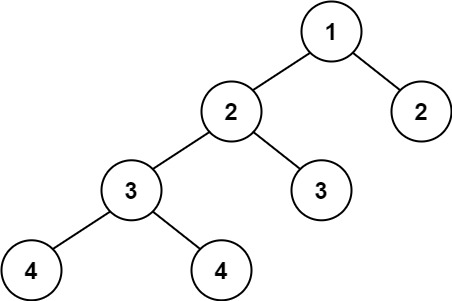
输入:root = [1,2,2,3,3,null,null,4,4] 输出:false示例 3:
输入:root = [] 输出:true提示:
- 树中的节点数在范围
[0, 5000]内-104 <= Node.val <= 104
首先得明确一个概念:什么是平衡二叉树。
平衡二叉树 是指该树所有节点的左右子树的深度相差不超过 1。
注意:是所有结点的左右子树,而不是根结点的左右子树。
思路:我们首先想到的就是求树的高度,然后相减判断差值是否大于1。
根结点做的事情:先判断根结点是不是平衡二叉树
// 限制条件
if (root == null) {
return true;
}
// 这个判断的是根结点
if (Math.abs(TreeNodeHigh(root.left) - TreeNodeHigh(root.right)) > 1) {
return false;
}框架:根结点判断完成再判断左右子树是否是平衡二叉树
// 递归判断左子树和右子树
if (!isBalanced(root.left)) {
return false;
}
return isBalanced(root.right);计算树的高度:
// 计算二叉树的高度
private int TreeNodeHigh(TreeNode root) {
if (root == null) {
return 0;
}
// 左子树的高度
int leftHigh = TreeNodeHigh(root.left);
// 右子树的高度
int rightHigh = TreeNodeHigh(root.right);
// 返回左子树和右子树的最大高度+根结点
return Math.max(leftHigh, rightHigh)+1;
}代码实现:
class Solution {
// 这个方法是用来判断一个二叉树是否为平衡二叉树的
// 而我们想要的是一个方法来计算这个二叉树的根结点的左右子树高度
public boolean isBalanced(TreeNode root) {
if (root == null) {
return true;
}
// 这个判断的是根结点
if (Math.abs(TreeNodeHigh(root.left) - TreeNodeHigh(root.right)) > 1) {
return false;
}
// 递归判断左子树和右子树
if (!isBalanced(root.left)) {
return false;
}
return isBalanced(root.right);
}
// 计算二叉树的高度
private int TreeNodeHigh(TreeNode root) {
if (root == null) {
return 0;
}
// 左子树的高度
int leftHigh = TreeNodeHigh(root.left);
// 右子树的高度
int rightHigh = TreeNodeHigh(root.right);
// 返回左子树和右子树的最大高度+根结点
return Math.max(leftHigh, rightHigh)+1;
}
}上述代码有不足的地方:重复计算比较多。当根结点是平衡二叉树时,就需要计算根结点左子树的左右子树的高度,而这部分的高度是我们在第一次计算时,就已经计算过了。因此我们就可以保留上一次计算的值,也就是存起来或者说记录上次计算的值,看看满不满足我们的要求。如下所示:
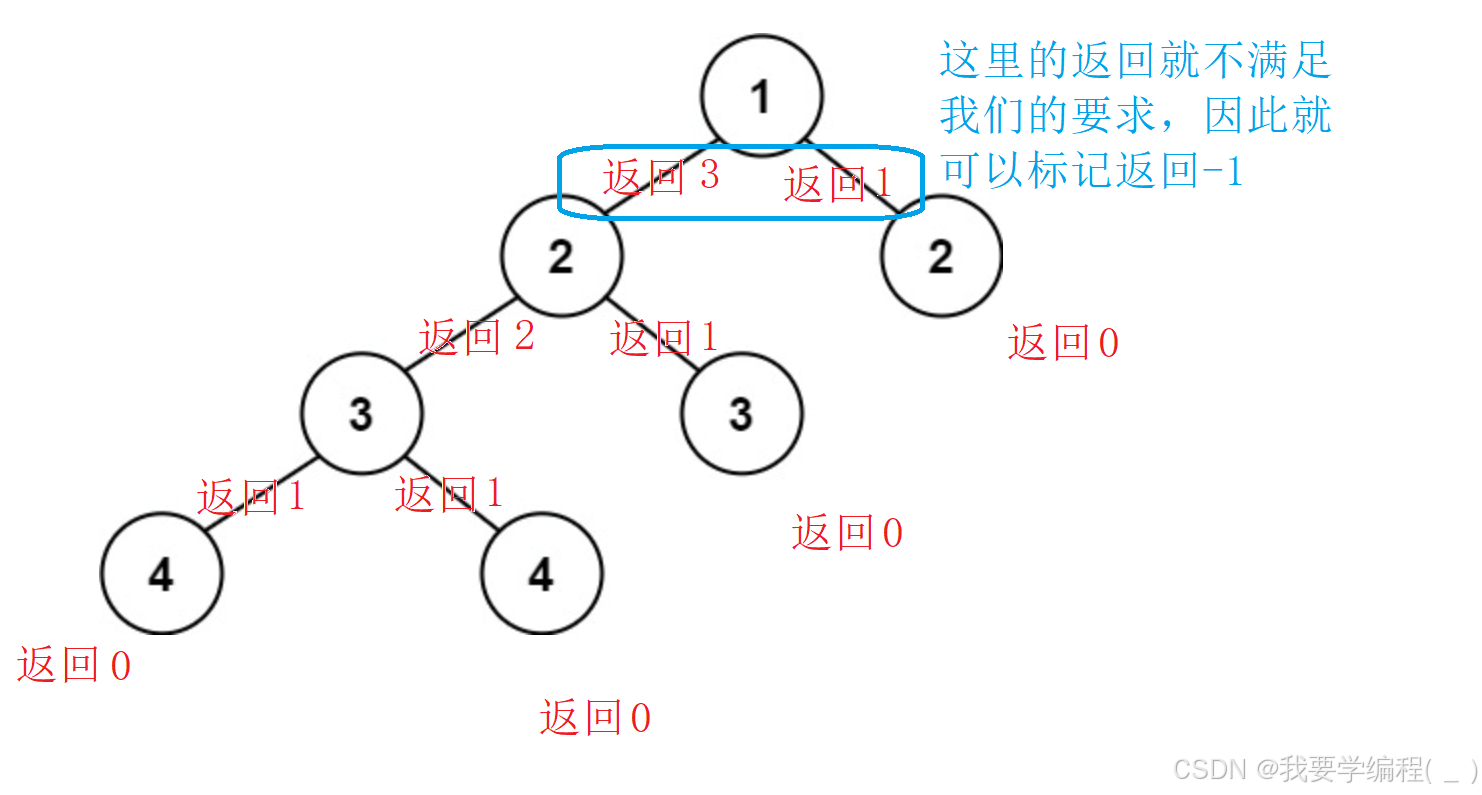
代码实现:
class Solution {
public boolean isBalanced(TreeNode root) {
if (root == null) {
return true;
}
// 因为返回值就三种:<0 ==0 >0 最后就比较看是否符合情况
return TreeNodeHigh(root) >= 0;
}
private int TreeNodeHigh(TreeNode root) {
if (root == null) {
return 0;
}
int leftHigh = TreeNodeHigh(root.left);
// 如果不符合要求了,就返回-1(标记)
if (leftHigh < 0) {
return -1;
}
int rightHigh = TreeNodeHigh(root.right);
// 符合要求(高度差符合平衡二叉树且右边的高度大于0)就返回高度
if (rightHigh >= 0 && Math.abs(leftHigh - rightHigh) <= 1) {
return Math.max(leftHigh, rightHigh) + 1 ;
} else {
// 不符合(高度差大于1或者右边的高度也是负数)就返回-1
return -1;
}
}
}这种方法还是大佬才能想到的。我们一般把第一种的普通递归思路写出来就行。
牛客网——JZ36 二叉搜索树与双向链表
题目:
描述
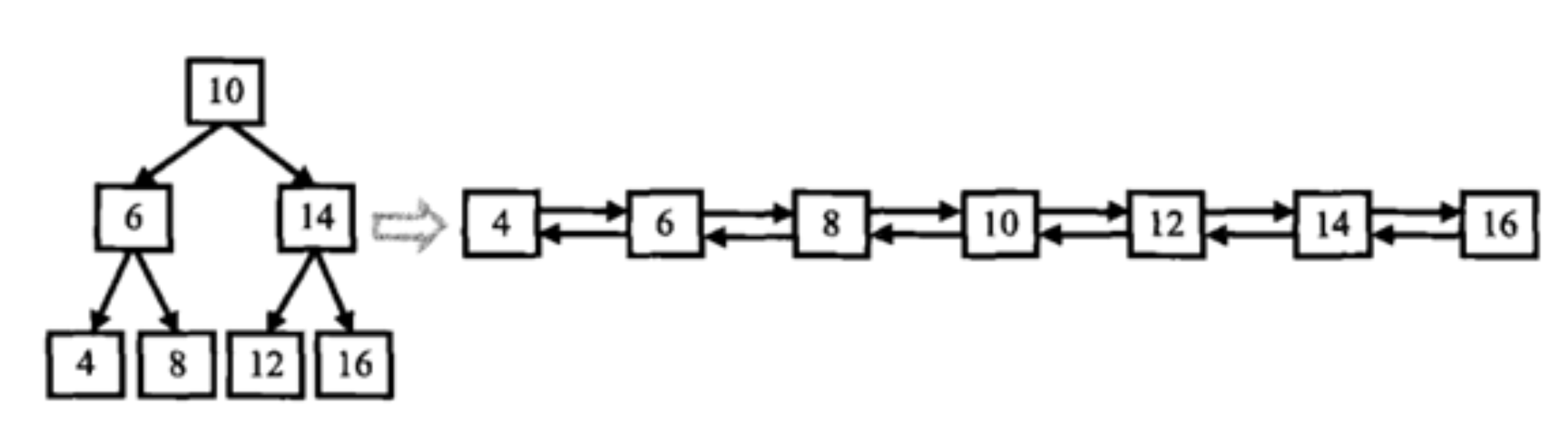
输入一棵二叉搜索树,将该二叉搜索树转换成一个排序的双向链表。如下图所示
数据范围:输入二叉树的节点数 0≤𝑛≤10000≤n≤1000,二叉树中每个节点的值 0≤𝑣𝑎𝑙≤10000≤val≤1000
要求:空间复杂度𝑂(1)O(1)(即在原树上操作),时间复杂度 𝑂(𝑛)O(n)
注意:
1.要求不能创建任何新的结点,只能调整树中结点指针的指向。当转化完成以后,树中节点的左指针需要指向前驱,树中节点的右指针需要指向后继
2.返回链表中的第一个节点的指针
3.函数返回的TreeNode,有左右指针,其实可以看成一个双向链表的数据结构4.你不用输出双向链表,程序会根据你的返回值自动打印输出
输入描述:
二叉树的根节点
返回值描述:
双向链表的其中一个头节点。
示例1
输入:
{10,6,14,4,8,12,16}返回值:
From left to right are:4,6,8,10,12,14,16;From right to left are:16,14,12,10,8,6,4;说明:
输入题面图中二叉树,输出的时候将双向链表的头节点返回即可。示例2
输入:
{5,4,#,3,#,2,#,1}返回值:
From left to right are:1,2,3,4,5;From right to left are:5,4,3,2,1;说明:
5 / 4 / 3 / 2 / 1 树的形状如上图
二叉搜索树的概念:树上每个节点的左子树的根结点的值小于根结点的值小于右子树的根结点的值。因此,当我们去用中序遍历去遍历这棵树时,其输出的结果的就是一个有序的数据。
思路:既然是要变成一个有序的双向链表,那么我们就可以从这里得出一些有用的信息。肯定是以中序遍历的方式去遍历这棵二叉树。修改的话,以 left 作为 prev 指针,以 right 作为 next 指针。那么我们就可以写一个二叉树中序遍历的方法出来,通过中序遍历来修改二叉树的指向。
下面是递归的核心代码:
// 中序遍历修改二叉树的指向
private void inOrder(TreeNode root) {
// 左子树 根 右子树
if (root == null) { // 限制条件
return;
}
// 左子树
inOrder(root.left);
// 修改根结点的指向
......
// 右子树
inOrder(root.right);
} 当 root 走到 4 这个节点时(上面描述的图),就可以修改其 left 与 right 的值,因为这里需要一个不断变化的值来指向 left 和 right 要修改的对象,因此就可以定义一个 prev 指针来指向要修改的前一个节点,那么就可以解决修改指针的问题。
代码实现:
public class Solution {
private TreeNode prev; // 默认是null
public TreeNode Convert(TreeNode pRootOfTree) {
if (pRootOfTree == null) {
return null;
}
// 修改二叉树为有序的双向链表
inOrder(pRootOfTree);
// 找到头结点并返回
TreeNode head = pRootOfTree;
// 一直找到 head.left == null 即可(沿着10找到4)
while (head.left != null) {
head = head.left;
}
return head;
}
// 中序遍历修改二叉树的指向
private void inOrder(TreeNode root) {
// 左子树 根 右子树
if (root == null) { // 限制条件
return;
}
// 左子树
inOrder(root.left);
// 修改根结点的指向
// 第一三行代码都执行时,是这样:4.left = prev 4.right = 6
root.left = prev;
if (prev != null) {
prev.right = root;
}
// 更新prev的值(不断的指向root的前一个结点)
prev = root;
// 右子树
inOrder(root.right);
}
}牛客网——KY11 二叉树遍历
描述
编一个程序,读入用户输入的一串先序遍历字符串,根据此字符串建立一个二叉树(以指针方式存储)。 例如如下的先序遍历字符串: ABC##DE#G##F### 其中“#”表示的是空格,空格字符代表空树。建立起此二叉树以后,再对二叉树进行中序遍历,输出遍历结果。
输入描述:
输入包括1行字符串,长度不超过100。
输出描述:
可能有多组测试数据,对于每组数据, 输出将输入字符串建立二叉树后中序遍历的序列,每个字符后面都有一个空格。 每个输出结果占一行。
示例1
输入:
abc##de#g##f###输出:
c b e g d f a
注意:这里给了我们前序遍历的结果,并且把空树的位置告诉我们了,因此这里可以只通过前序遍历来创建一棵唯一的二叉树。
思路:既然给了我们前序遍历的结果,那么我们肯定是要通过前序遍历来创建二叉树。即先创建根结点,再创建左子树,再创建右子树。核心代码思路出来了,也就可以开始写了。
代码实现:
import java.util.Scanner;
// 创建树的节点
class TreeNode {
public char val;
public TreeNode left;
public TreeNode right;
public TreeNode(char val) {
this.val = val;
}
}
// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
// 注意 hasNext 和 hasNextLine 的区别
while (in.hasNextLine()) { // 注意 while 处理多个 case
String str = in.nextLine();
// 以前序遍历的方式来创建二叉树
TreeNode root = createTree(str);
// 中序遍历二叉树
inOrder(root);
}
}
// 递归创建二叉树
public static int i; // 记录遍历的位置
public static TreeNode createTree(String str) {
// 根据前序遍历创建二叉树:根 左子树 右子树
TreeNode root = null;
char ch = str.charAt(i);
if (ch != '#') {
// 这里不是空树,创建树:根 左子树 右子树
root = new TreeNode(ch);
i++; // 创建完成,就要往后走
// 左子树
root.left = createTree(str);
// 右子树
root.right = createTree(str);
} else {
// 因为root已经初始化,这里只需要让i往后走即可
i++;
}
return root;
}
public static void inOrder(TreeNode root) {
if (root == null) {
return;
}
// 根 左子树 右子树
inOrder(root.left);
System.out.print(root.val+" ");
inOrder(root.right);
}
}二叉树的创建中根结点做的事情: 就是创建根结点即可。其余的就是交给框架去递归创建左子树和右子树。
注意:这里在创建二叉树时,i 由于是 static 修饰,只有一份。当我们再次去创建一棵二叉树时,这个 i 的值不会从 0 开始,因此我们的处理方法有两种:
1、在每次创建完一棵二叉树之后,把 i 置为 0即可。
2、尽量不要用 static 修饰的变量。但是这里受题目限制,只能用这个了,而且这里的测试用例很可能只有一个
好啦!本期 数据结构之初始二叉树(3)的刷题篇(上)的学习之旅就到此结束啦!我们下一期再一起学习吧!