前言：哈喽小伙伴们，上篇文章我们讲述了一个特殊的二叉树——使用数组实现的堆的基本知识之后呢，从这篇文章开始，我们就正式进入普通二叉树的介绍啦，二叉树真正的难点——递归，即将来临，小伙伴们注意不要掉队哦。

一.链式二叉树

在前边的文章中，我们已经了解到，二叉树可以有顺序存储和链式存储两种方式，在堆的文章中，我们讲解了顺序存储的完全二叉树，那么现在，我们一起来认识一下链式存储的普通二叉树。

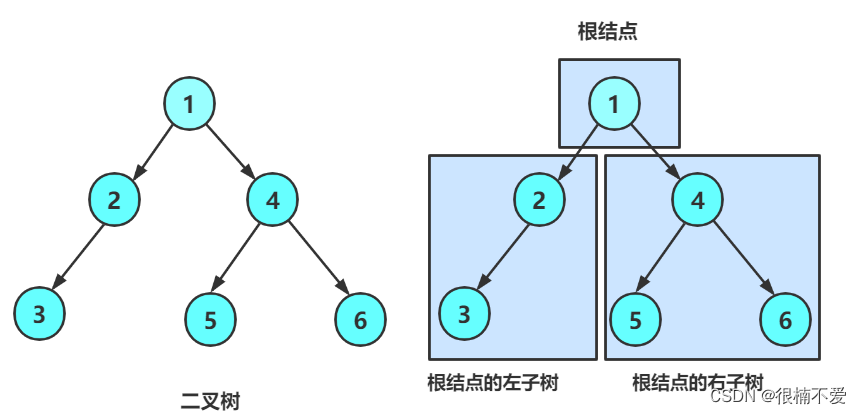
我们知道，二叉树的规则是，每个节点至多有两个子节点，而两个子节点及其后续的子节点组成的整体，又可以分别称为左右子树，如右图所示，1为根节点，2和3则一起构成左子树，4、5、6则构成右子树。 而这两个子树，同样可以看做是由一个根节点和左右子树构成的新树。

所以，任何一个二叉树都可以被拆解为三部分：

1. 根节点
2. 左子树
3. 右子树

由此看来，二叉树和递归离不开关系，后续二叉树的各种基本操作，也都是通过递归来实现的。

---

二.遍历二叉树

 二叉树的遍历有三种方式：

1.前（先）序遍历：先遍历树的根节点，再遍历它的左子树，最后是右子树。

2.中序遍历：先遍历树的左子树，再遍历它的根节点，最后是右子树。

3.后序遍历：先遍历树的左子树，再遍历它的右子树，最后是根节点。

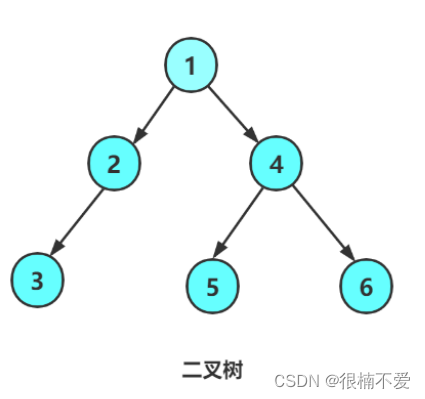
我们以这棵树为例：

前序遍历即为：1 2 3 4 5 6。

但是这样写其实并不合理，因为我们是用链表来写二叉树的结构的，所以对于节点2来说，它并不是没有右子树，而是右子树是空树。

同样的，3、5、6同样可以作为一颗树，不过它们的左右子树都是空树罢了。

所以合理的遍历方式应该把空树也带上，我们这里用N表示，于是：

前序遍历：1    2    3    N    N    N    4    5    N    N    6    N    N，如果用图形来表示，如下：

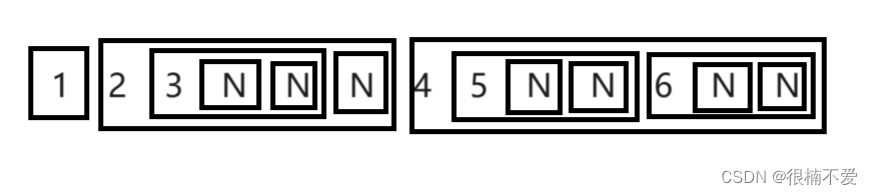
每一个方框都可以看做是一个新的树，从左到右依次为：根，左，右。如此，我们便也能写出中序遍历和后序遍历：

中序遍历：N    3    N    2    N    1    N    5    N    4    N    6    N，图形如下：

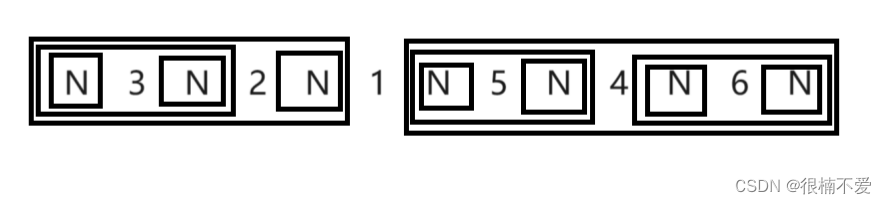
后序遍历：N    N    3    N    2    N    N    5    N    N    6    4    1，图形如下：

了解了二叉树的基本架构之后，我们就开始来实现二叉树的各个功能啦。

---

三.二叉树的实现

1.二叉树的定义

typedef int BTDataType;

typedef struct TreeNode
{
	BTDataType data;
	struct TreeNode* left;
	struct TreeNode* right;
}TreeNode;

二叉树的定义并不难写，需要数据变量，以及指向左子树和右子树的两个指针。

---

2.创建二叉树节点

//创建树节点
TreeNode* CreateTreeNode(TreeNode* root,BTDataType x)
{
	TreeNode* tmp = (TreeNode*)malloc(sizeof(TreeNode));
	if (tmp == NULL)
	{
		perror("CreateTree->malloc");
		exit(-1);
	}
	root = tmp;
	root->data = x;
	root->left = NULL;
	root->right = NULL;
	return root;
}

二叉树节点的创建也不难，起初我们需要将两个指针都指向NULL。

为了方便下文对二叉树的操作进行讲解，我们手动创建一颗如下的二叉树：

	TreeNode root;
	TreeNode* node1 = CreateTreeNode(&root, 1);
	TreeNode* node2 = CreateTreeNode(&root, 2);
	TreeNode* node3 = CreateTreeNode(&root, 3);
	TreeNode* node4 = CreateTreeNode(&root, 4);
	TreeNode* node5 = CreateTreeNode(&root, 5);
	TreeNode* node6 = CreateTreeNode(&root, 6);
	node1->left = node2;
	node1->right = node4;
	node2->left = node3;
	node4->left = node5;
	node4->right = node6;

---

四.二叉树的操作

二叉树的操作，基本上都和递归紧密相连。

1.先序遍历

先序遍历，也就是按照：根，左子树，右子树的顺序遍历，下面我直接给出代码：

//先序遍历
void PrevOrder(TreeNode* root)
{
	if (root == NULL)
	{
		printf("N ");
		return;
	}
	printf("%d ", root->data);//根
	PrevOrder(root->left);//左子树
	PrevOrder(root->right);//右子树
}

没错，代码就是这么简单。

想要按照我们上边所讲解的遍历方法进行二叉树的遍历，递归是最好的选择。

我们来分析以下：

首先，如果我们遇到叶节点，那么他就没有左右子树，这时候我们再去递归调用它的左右子树时，就打印一个N，证明我们遇到了空节点。

随后，我们按照根，左，右的顺序，先打印根节点的数据，再先后去递归打印它的左右子树的节点数据。

递归确实是一个难以理解的重点知识，但是博主却有一个小妙招，可以分享给大家：

我们继续来看上边的代码，如果我去掉递归调用，那么我剩下的代码是：

void PrevOrder(TreeNode* root)
{
	if (root == NULL)
	{
		printf("N ");
		return;
	}
	printf("%d ", root->data);//根
}

这样就可以看做是一个打印节点数据的代码。

那么我在打印完根节点的数据之后，想打印它左子树的根节点数据，就把它左子树的地址传给这个函数，也就是：

    PrevOrder(root->left);//左子树

打印完左子树，再去打印右子树，于是就把右子树的地址传过去：

    PrevOrder(root->right);//右子树

 要记住的是，每当我们用递归调用时，都是一层一层的套用该函数，直到遇到某个限制条件，到达最后一层时，才会终止当前的函数，并返回上一层函数，直到返回至第一层为止。

来看结果：

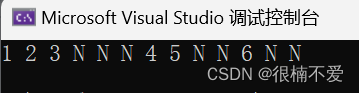
而中序，后序遍历，就和上边是大差不差，只需要改变递归调用函数的顺序。

---

2.中序遍历

中序遍历的顺序为：左子树，根，右子树，所以：

//中序遍历
void InOrder(TreeNode* root)
{
	if (root == NULL)
	{
		printf("N ");
		return;
	}
	InOrder(root->left);//左子树
	printf("%d ", root->data);//根
	InOrder(root->right);//右子树
}

先递归调用左子树，再打印根节点数据，再递归调用右子树。

结果如下：

---

3.后序遍历

后序遍历的顺序为：左子树，右子树，根，所以：

//后序遍历
void PostOrder(TreeNode* root)
{
	if (root == NULL)
	{
		printf("N ");
		return;
	}
	PostOrder(root->left);//左子树
	PostOrder(root->right);//右子树
	printf("%d ", root->data);//根
}

在左右子树全部都递归调用之后，再打印根节点数据。

结果如下：

---

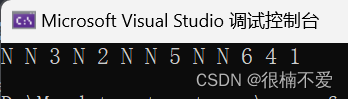
4.节点个数

二叉树的节点个数该怎么统计呢？？？

有小伙伴会说，这简单啊，用个计数器，遍历的时候顺便计数不就好啦。

这确实是一种方法，但是却不够简便，我们不妨来思考思考有没有更简单一点的方法：

二叉树的节点个数，是不是就等于它的根节点，加上它的左子树，右子树的节点个数？

那我就能得出下边的代码：

//节点个数
int TreeSize(TreeNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	return TreeSize(root->left) + TreeSize(root->right) + 1;
}

结果如下：

 

简不简单就问你？有没有问题？

如果根节点为空，就说明是空树，节点个数为0，返回0；

如果不是空树，那我就返回左子树的节点个数+右子树的节点个数 + 根节点（也就是1）。

怎么样？有没有被递归给圈粉？递归是如此的奇妙。 

---

递归分析

递归问题的基本思想就是把大型的，复杂的问题拆解成多个子问题，简单的问题。

以上述代码为例，我们要求出一个二叉树的节点个数，而这棵二叉树又可以拆解为一个一个的子二叉树，我们将每个子树的节点个数统计出来，在整合起来，就得出了总的节点个数。 

当我们面对递归问题时，要做的就是找到递归的两个要点：

1. 终止条件
2. 递归部分

拿上述代码为例，终止条件就是：

    if (root == NULL)
    {
        return 0;
    }

而递归部分就是：

    return TreeSize(root->left) + TreeSize(root->right) + 1;

---

5.叶节点数

叶节点也就是左右子树都为空的节点，那么叶节点个数该怎么求呢？

很显然，与上边的想法类似，也就是左子树的叶节点个数+右子树的叶节点个数。

如此一来，我们便能写出代码：

//叶节点个数
int TreeLeafSize(TreeNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	if (root->left == NULL && root->right == NULL)
	{
		return 1;
	}
	return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}

当为空树时，自然没有叶节点，返回0；

当根节点存在，且它的左右子树都为空时，说明它是叶节点，返回1；

上述两种都不满足，则返回左右子树叶节点之和，实现递归。

结果如下：

---

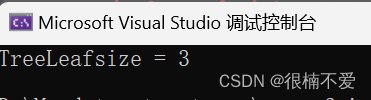
6.树的高度

二叉树的高度，也可以叫做深度、层数。

2那么该如何求出二叉树的高度呢？？？

我们仍然利用上边的思想，把根和左右子树独立开，不难得出，求树的高度就可以变成求左右两棵子树的高度较大的那一个再 + 1。

//树高度
int TreeHight(TreeNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	int lefthight = TreeHight(root->left);
	int righthight = TreeHight(root->right);
	return lefthight > righthight ? lefthight + 1 : righthight + 1;
}

首先仍然是要判断是否为空树。

然后我们要把左右子树的高度定义出来。

最后我们使用三目运算符来实现比较左右子树的高度并进行返回。

结果如下：

---

7.第k层节点数

二叉树还有一种操作，那就是求其某一层的节点数，这该怎么求呢？？？

有一种写法是，分别求二叉树的前k层和前k-1层，再相减，但是这显然会非常麻烦。

所以，我们仍然可以采用把我们上边的递归思想：

求二叉树的第k层，可以等价为是求其左右子树的第k-1层节点数之和。

//第k层的节点个数
int LeveKSize(TreeNode* root,int k)
{
	assert(k > 0);
	if (root == NULL)
	{
		return 0;
	}
	if (k == 1)
	{
		return 1;
	}
	return LeveKSize(root->left, k - 1) + LeveKSize(root->right, k - 1);
}

当k = 1时，即第一层，只有一个根节点，返回1，反之就返回其左右子树的第k-1层节点数之和。

来看结果：

首先是第三层，有3个节点；

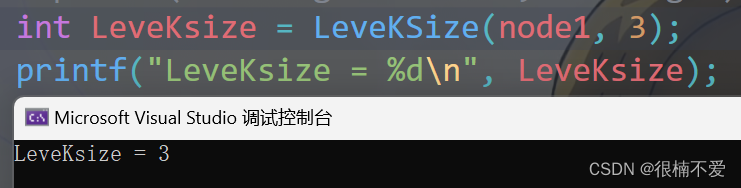
 然后是第四层，没有节点：

---

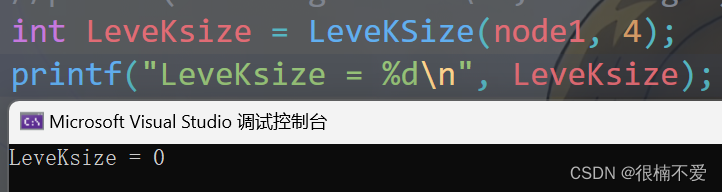
8.查找指定值节点

对于二叉树，同样有查找给定的值的节点的操作，并返回它的地址，这又该如何实现呢？？？

很明显，如果这个值不是根节点，就要让左右子树去分别查找：

// 二叉树查找值为x的节点
TreeNode* BinaryTreeFind(TreeNode* root, BTDataType x)
{
	if (root == NULL)
		return NULL;

	if (root->data == x)
		return root;

	TreeNode* ret = BinaryTreeFind(root->left, x);
	if (ret)
		return ret;

	return BinaryTreeFind(root->right, x);
}

首先判断空树。

然后判断根节点的值是否为要查找的数据，是就直接返回根节点地址，反之就开始查找左右子树。

我们先查找左子树，这里要注意一点，要临时定义一个指针变量来判断左子树中是否能找到节点。

如果存在，就会返回其地址，不存在，ret就为空，这样我们就接着去查找右子树。

---

 

9.销毁二叉树

二叉树该如何销毁呢？？？

是从根节点开始一个一个遍历销毁吗？？？但是这样每销毁一个根节点，我们都要先去记录它的两个左右子树的地址，未免有点太麻烦了些。

既然不能从上到下，那我们就从下到上呗，不要忘了，还有后序遍历呢。

//销毁树
void TreeDestroy(TreeNode* root)
{
	if (root == NULL)
		return;
	TreeDestroy(root->left);
	TreeDestroy(root->right);
	free(root);
}

---

四.完整代码展示

1.BinaryTree.h

#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#include<assert.h>

typedef int BTDataType;

typedef struct TreeNode
{
	BTDataType data;
	struct TreeNode* left;
	struct TreeNode* right;
}TreeNode;


//创建树
TreeNode* CreateTreeNode(TreeNode* root,BTDataType x);
//销毁树
void TreeDestroy(TreeNode* root);
//先序遍历
void PrevOrder(TreeNode* root);
//中序遍历
void InOrder(TreeNode* root);
//后序遍历
void PostOrder(TreeNode* root);
// 层序遍历
void LevelOrder(TreeNode* root);
//节点个数
int TreeSize(TreeNode* root);
//叶节点个数
int TreeLeafSize(TreeNode* root);
//树高度
int TreeHight(TreeNode* root);
//第k层的节点个数
int LeveKSize(TreeNode* root,int k);
// 二叉树查找值为x的节点
TreeNode* BinaryTreeFind(TreeNode* root, BTDataType x);

---

2.BinaryTree.c

#include "BinaryTree.h"

//创建树节点
TreeNode* CreateTreeNode(TreeNode* root,BTDataType x)
{
	TreeNode* tmp = (TreeNode*)malloc(sizeof(TreeNode));
	if (tmp == NULL)
	{
		perror("CreateTree->malloc");
		exit(-1);
	}
	root = tmp;
	root->data = x;	
	root->left = NULL;
	root->right = NULL;
	return root;
}
//销毁树
void TreeDestroy(TreeNode* root)
{
	if (root == NULL)
		return;
	TreeDestroy(root->left);
	TreeDestroy(root->right);
	free(root);
}
//先序遍历
void PrevOrder(TreeNode* root)
{
	if (root == NULL)
	{
		printf("N ");
		return;
	}
	printf("%d ", root->data);//根
	PrevOrder(root->left);//左子树
	PrevOrder(root->right);//右子树
}
//中序遍历
void InOrder(TreeNode* root)
{
	if (root == NULL)
	{
		printf("N ");
		return;
	}
	InOrder(root->left);//左子树
	printf("%d ", root->data);//根
	InOrder(root->right);//右子树
}
//后序遍历
void PostOrder(TreeNode* root)
{
	if (root == NULL)
	{
		printf("N ");
		return;
	}
	PostOrder(root->left);//左子树
	PostOrder(root->right);//右子树
	printf("%d ", root->data);//根
}
//节点个数
int TreeSize(TreeNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	return TreeSize(root->left) + TreeSize(root->right) + 1;
}
//叶节点个数
int TreeLeafSize(TreeNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	if (root->left == NULL && root->right == NULL)
	{
		return 1;
	}
	return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}
//树高度
int TreeHight(TreeNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	int lefthight = TreeHight(root->left);
	int righthight = TreeHight(root->right);
	return lefthight > righthight ? lefthight + 1 : righthight + 1;
}
//第k层的节点个数
int LeveKSize(TreeNode* root,int k)
{
	assert(k > 0);
	if (root == NULL)
	{
		return 0;
	}
	if (k == 1)
	{
		return 1;
	}
	return LeveKSize(root->left, k - 1) + LeveKSize(root->right, k - 1);
}
// 二叉树查找值为x的节点
TreeNode* BinaryTreeFind(TreeNode* root, BTDataType x)
{
	if (root == NULL)
		return NULL;

	if (root->data == x)
		return root;

	TreeNode* ret = BinaryTreeFind(root->left, x);
	if (ret)
		return ret;

	return BinaryTreeFind(root->right, x);
}

---

3.test.c

#include "BinaryTree.h"

int main()
{
    TreeNode root;
    TreeNode* node1 = CreateTreeNode(&root, 1);
    TreeNode* node2 = CreateTreeNode(&root, 2);
    TreeNode* node3 = CreateTreeNode(&root, 3);
    TreeNode* node4 = CreateTreeNode(&root, 4);
    TreeNode* node5 = CreateTreeNode(&root, 5);
    TreeNode* node6 = CreateTreeNode(&root, 6);
    node1->left = node2;
    node1->right = node4;
    node2->left = node3;
    node4->left = node5;
    node4->right = node6;
    //PrevOrder(node1);
    //printf("\n");
    //InOrder(node1);
    //printf("\n");
    //PostOrder(node1);
    //printf("\n");
    //int Treesize = TreeSize(node1);
    //printf("Treesize = %d\n", Treesize);
    //int TreeLeafsize = TreeLeafSize(node1);
    //printf("TreeLeafsize = %d\n", TreeLeafsize);
    //int Treehight = TreeHight(node1);
    //printf("Treehight = %d\n", Treehight);
    int LeveKsize = LeveKSize(node1, 4);
    printf("LeveKsize = %d\n", LeveKsize);
    TreeDestroy(node1);
    node1 = NULL;
    return 0;
}

---

五.总结

二叉树的基本知识和操作到这里就结束啦，二叉树与递归关系颇深。

虽然博主对于递归讲解的也不是那么清晰透彻，但是递归的知识真的是要靠自己一步一步的去理解，去深入。

希望小伙伴们都可以努力去拿下递归，这是每一个优秀程序员都必须要克服的！！！