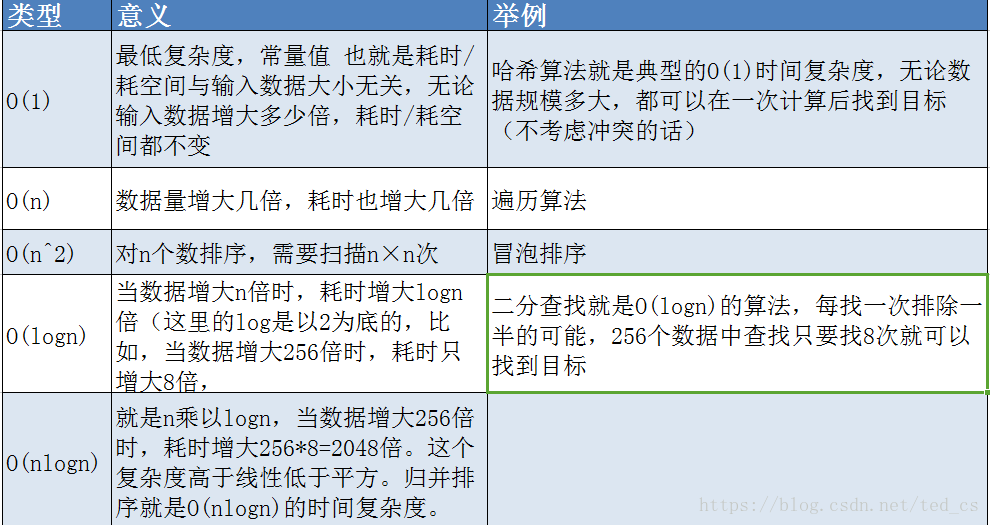
常见排序算法及其时间复杂度
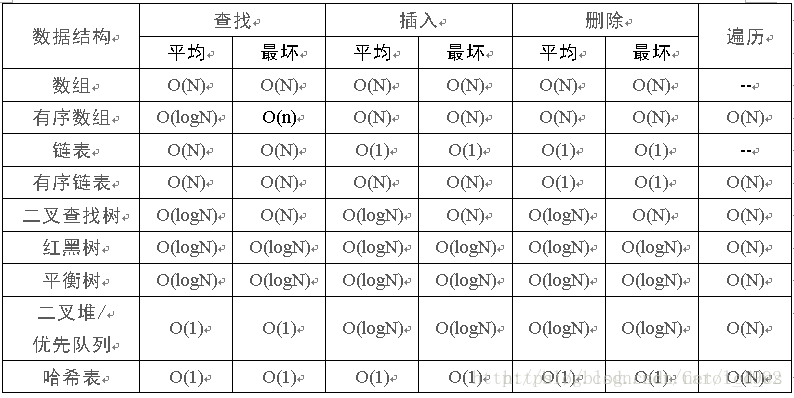
C++ STL容器时间复杂度|
上述四种容器采用红黑树实现,红黑树是平衡二叉树的一种。不同操作的时间复杂度近似为:
插入: O(logN)
查看:O(logN)
删除:O(logN)
hash_map, hash_set, hash_multimap, and hash_multiset
上述四种容器采用哈希表实现,不同操作的时间复杂度为:
插入:O(1),最坏情况O(N)。
查看:O(1),最坏情况O(N)。
删除:O(1),最坏情况O(N)。
记住,如果你采用合适的哈希函数,你可能永远不会看到最坏情况。但是记住这一点是有必要的。
程序的时间复杂度计算
时间复杂度的概念。
定义:存在常数 c 和函数 f(N),使得当 N >= c 时 T(N) <= f(N),表示为 T(n) = O(f(n)) 。
很多时候一眼就能看出程序的时间复杂度,但是遇到复杂的就需要将其过程推导出来,为此总结以下两种形式
一、循环主体中的变量参与循环条件的判断
找出主体语句中与T(n)成 正比的循环变量,带入进行计算,例如:
int i = 1;
while(i <= n)
i = i*2;
其中i*2的次数与T(n)成正比,则2的T(n)次方<= n,则T(n)<=log2n。
二、循环主体中的变量与循环条件无关
可采用数学归纳法或者直接累计循环次数,多层循环时从内到外分析,只关注主体语句执行次数。这种情况分为递归程序和非递归程序
递归程序一般使用公式进行递推,例如:
int fact (int n){
if(n<=1) return 1;
return n*fact(n-1);
}
T(n)=1+T(n-1)=1+1+T(n-2)= ...=n-1+T(1)
则T(N)=O(n).
非递归程序比较简单,可以直接累计次数
计算时间复杂度--(简单版)
步骤:
1、找到执行次数最多的语句
2、语句执行语句的数量级
3、用O表示结果
计算时间复杂度的3个出发点,掌握这三个出发点,那么一向搞不懂的时间复杂度就可以迎刃而解啦。
然后:
1、用常数1取代运行时间中的所有加法常数
2、在修改后的运行次数函数中,只保留最高阶项
3、如果最高阶项存在且不是1,那么我们就去除于这个项相乘的常数。比如3n^2我们取n^2
最后就可以得到你们想要的结果了。
举几个例子:
我们来看一下这个例子,用的是java,内容就是打印8条语句,问这个程序的时间复杂度是多少?
public class TS {
public static void main(String[] args) {
System.out.println("111");
System.out.println("111");
System.out.println("111");
System.out.println("111");
System.out.println("111");
System.out.println("111");
System.out.println("111");
System.out.println("111");
}
}
O(8)? 当然不是!!!按照时间复杂度的概念“T(n)是关于问题规模为n的函数”,这里跟问题规模有关系吗?没有关系,用我们的第一个方法,时间复杂度为O(1)。
第二个例子:(线性阶)
public class TS {
public static void main(String[] args) {
int sum = 0;
for(int i=1;i<=100;i++) {
sum = sum + i;
}
}
}
时间复杂度为O(n)。
第三个例子:(平方阶)
public class TS {
public static void main(String[] args) {
int sum = 0;
for(int i=1;i<=100;i++) {
for(int j=1;j<=100;j++)
sum = sum + i;
}
}
}
外层i的循环执行一次,内层j的循环就要执行100次,所以外层执行100次,那么总的就需要执行100*100次,那么n次呢?就是n的平方次了。所以时间复杂度为:O(n^2)。
平方阶的另外一个例子:
public class TS {
public static void main(String[] args) {
int sum = 0;
for(int i=1;i<=100;i++) {
for(int j=i;j<=100;j++)
sum = sum + i;
}
}
}
当i=1的时候执行n次,当n=2的时候执行(n-1)次,......
一直这样子下去就可以构造出一个等差数列:n+(n-1)+(n-2)+......+2+1
根据等差数列的求和公式:或者
求和易得:n+n*(n-1)/2整理一下就是n*(n+1)/2然后我们将其展开可以得到n^2/2+n/2。
根据我们的步骤走,保留最高次项,去掉相乘的常数就可以得到时间复杂度为:O(n^2)
第四个例子:(对数阶)
public class TS {
public static void main(String[] args) {
int i=1;
int n= 100;
while(i<n) {
i = i*2;
}
}
2^x = n,所以时间复杂度为O(log2n)。
补充常用的时间复杂度所耗费的时间从小到大依次是:
O(1 )< O(logn) < O(n) < O(n*logn) < O(n^2) < O(n^3) < O(2^n) < O(n!) < O(n^n)
最坏情况与平均情况:
平均运行时间是期望的运行时间。最坏的运行时间是一种保证。我们提到的运行时间都是最坏的运行时间。可以通过空间来换取时间。

