平衡二叉树(AVL树)
1.为什么要用平衡二叉树(AVL树)
看一个案例(说明二叉排序树可能的问题)
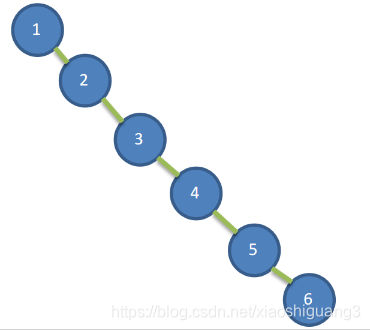
给你一个数列{1,2,3,4,5,6},要求创建一颗二叉排序树(BST), 并分析问题所在.
左边BST 存在的问题分析:
- 左子树全部为空,从形式上看,更像一个单链表.
- 插入速度没有影响
- 查询速度明显降低(因为需要依次比较), 不能发挥BST的优势,因为每次还需要比较左子树,其查询速度比单链表还慢
- 解决方案-平衡二叉树(AVL)
2.平衡二叉树基本介绍
平衡二叉树也叫平衡二叉搜索树(Self-balancing binary search tree)又被称为AVL树, 可以保证查询效率较高。
具有以下特点:它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。AVL树的查找、插入、删除操作在平均和最坏的情况下都是O(logn),这得益于它时刻维护着二叉树的平衡。平衡二叉树的常用实现方法有红黑树、AVL、替罪羊树、Treap、伸展树等。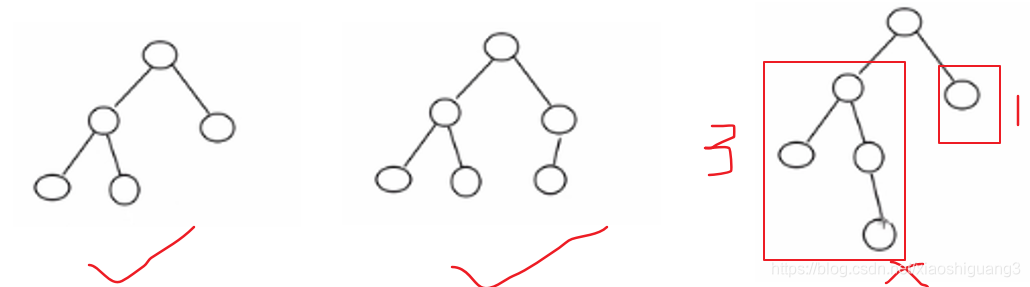
3.平衡二叉树的相关概念
-
平衡因子:将二叉树上节点的左子树高度减去右子树高度的值称为该节点的平衡因子BF(Balance Factor)。
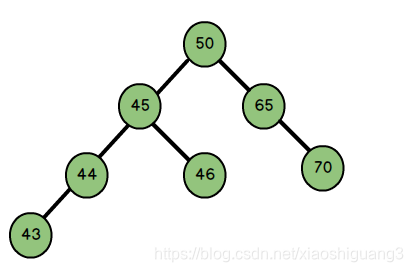
上图是一个平衡二叉树:
节点50的左子树高度为3,右子树高度为2,BF= 3-2 = 1;
节点45的左子树高度为2,右子树高度为1,BF= 2-1 = 1;
节点46的左子树高度为0,右子树高度为0,BF= 0-0 = 0;
节点65的左子树高度为0,右子树高度为1,BF= 0-1 = -1;
对于平衡二叉树,BF的取值范围为[-1,1]。如果发现某个节点的BF值不在此范围,则需要对树进行调整。
4.平衡二叉树的调整
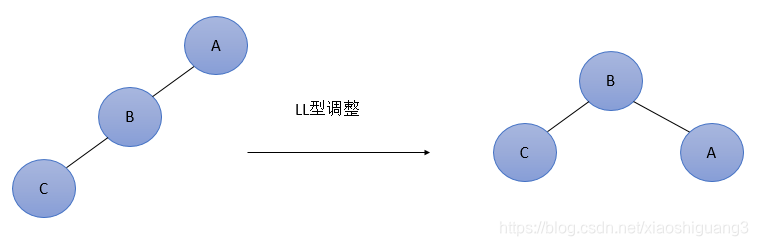
(1)LL型调整(右旋转,降低左子树的高度):
由于在A的左孩子(L)的左子树(L)上插入新结点,使原来平衡二叉树变得不平衡,此时A的平衡因子由1增至2。下图是LL型的最简单形式。显然,按照大小关系,结点B应作为新的根结点,其余两个节点分别作为左右孩子节点才能平衡,A结点就好像是绕结点B顺时针旋转一样。
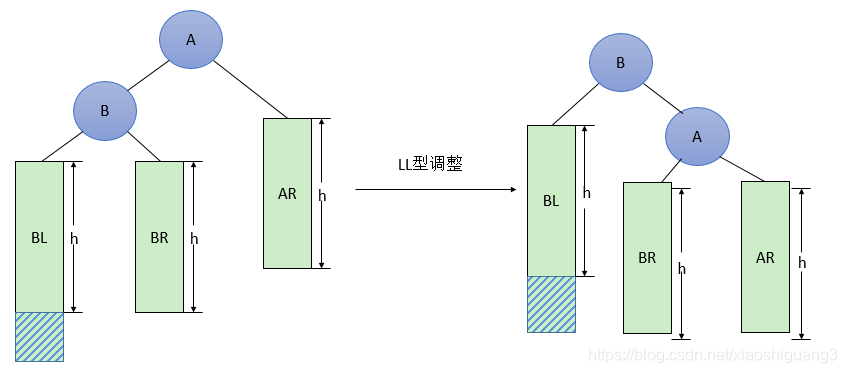
LL型调整的一般形式如下图所示,表示在A的左孩子B的左子树BL(不一定为空)中插入结点(图中阴影部分所示)而导致不平衡( h 表示子树的深度)。这种情况调整如下:
* A的左孩子B提升为新的根结点;
* ②将原来的根结点A降为B的右孩子;
* ③各子树按大小关系连接(BL和AR不变,BR调整为A的左子树)。
(2)RR型调整(左旋转,降低右子树的高度):
由于在A的右孩子(R)的右子树(R)上插入新结点,使原来平衡二叉树变得不平衡,此时A的平衡因子由-1变为-2。下是RR型的最简单形式。显然,按照大小关系,结点B应作为新的根结点,其余两个节点分别作为左右孩子节点才能平衡,A结点就好像是绕结点B逆时针旋转一样。

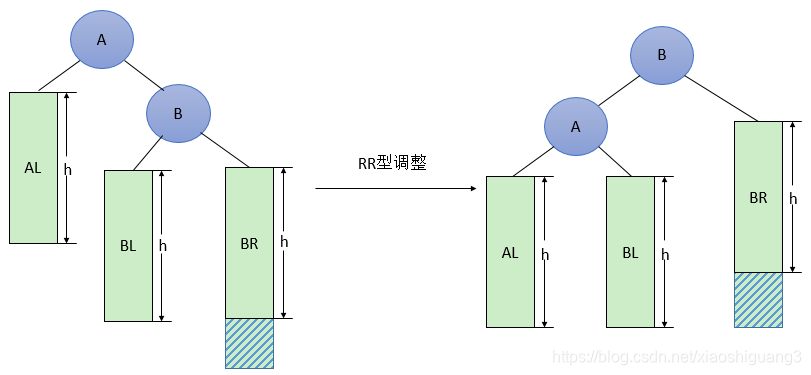
RR型调整的一般形式如下图所示,表示在A的右孩子B的右子树BR(不一定为空)中插入结点(图中阴影部分所示)而导致不平衡( h 表示子树的深度)。这种情况调整如下:
* 将A的右孩子B提升为新的根结点;
* 将原来的根结点A降为B的左孩子
* 子树按大小关系连接(AL和BR不变,BL调整为A的右子树)。
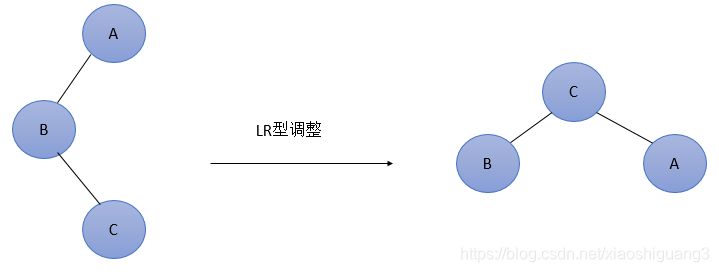
(3)LR型调整(先对当前结点的左子树进行左旋转,然后在对当前结点进行右旋转):
由于在A的左孩子(L)的右子树(R)上插入新结点,使原来平衡二叉树变得不平衡,此时A的平衡因子由1变为2。下图最简单形式。显然,按照大小关系,结点C应作为新的根结点,其余两个节点分别作为左右孩子节点才能平衡。
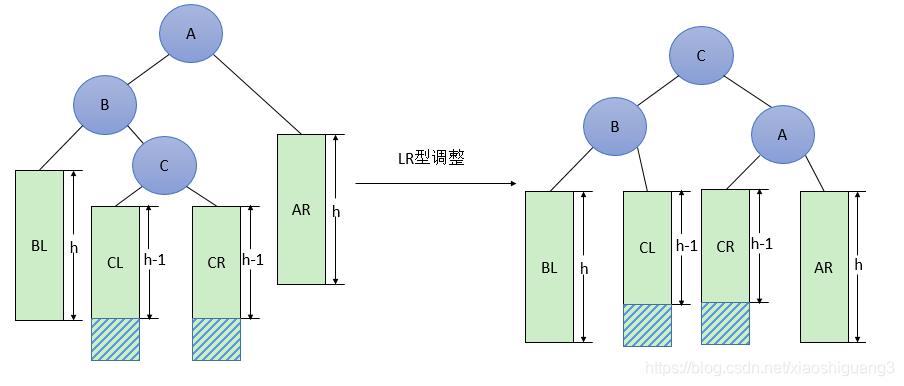
LR型调整的一般形式如下图6所示,表示在A的左孩子B的右子树(根结点为C,不一定为空)中插入结点(图中两个阴影部分之一)而导致不平衡( h 表示子树的深度)。这种情况调整如下:
①将B的左孩子C提升为新的根结点;
②将原来的根结点A降为C的右孩子;
③各子树按大小关系连接(BL和AR不变,CL和CR分别调整为B的右子树和A的左子树)。
(4)RL型调整(先对当前结点的右子树进行右转,然后在对当前结点进行左转):
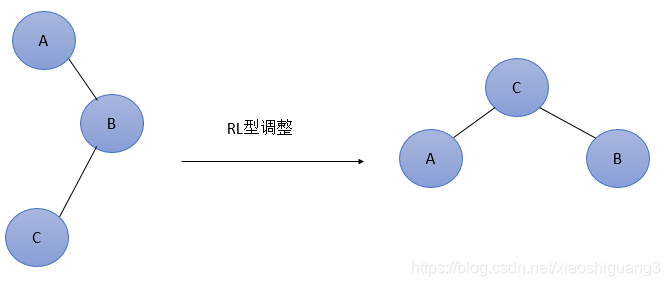
由于在A的右孩子(R)的左子树(L)上插入新结点,使原来平衡二叉树变得不平衡,此时A的平衡因子由-1变为-2。下图是RL型的最简单形式。显然,按照大小关系,结点C应作为新的根结点,其余两个节点分别作为左右孩子节点才能平衡。
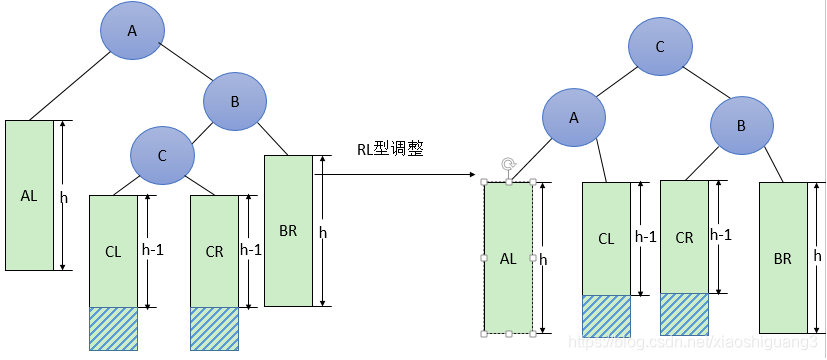
RL型调整的一般形式如下图8所示,表示在A的右孩子B的左子树(根结点为C,不一定为空)中插入结点(图中两个阴影部分之一)而导致不平衡( h 表示子树的深度)。这种情况调整如下:
①将B的左孩子C提升为新的根结点;
②将原来的根结点A降为C的左孩子;
③各子树按大小关系连接(AL和BR不变,CL和CR分别调整为A的右子树和B的左子树)。
5.平衡二叉树的实现
-
左旋转(单旋转,LL)

-
右旋转(单旋转,RR)

-
LR旋转
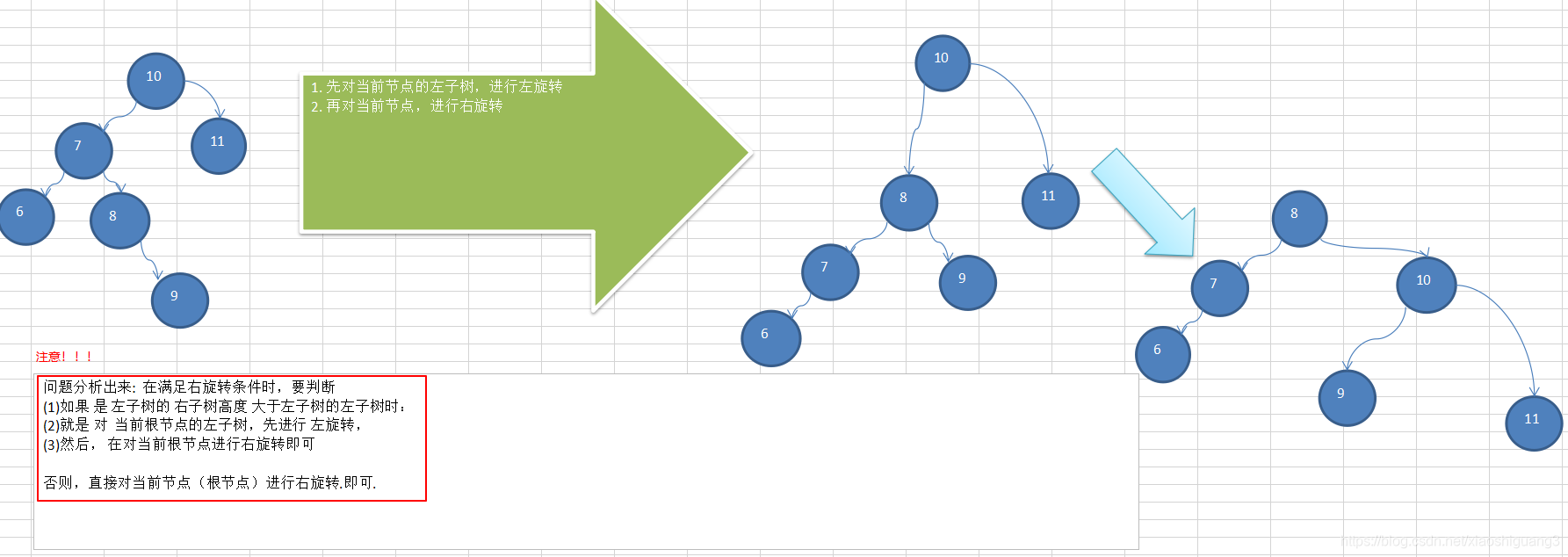
-
代码:
public class AvlTreeDemo {
public static void main(String[] args) {
// int[] arr = {4,3,6,5,7,8}; //左旋转
// int[] arr = {10,12, 8, 9, 7, 6}; //右旋转
int[] arr = {10, 11, 7, 6, 8, 9 }; //LR
// int[] arr = {2,1,6,5,7,3 }; //RL
// int[] arr = {1, 2, 3, 4, 5, 6, 7};
AvlTree avlTree = new AvlTree();
for (int i = 0; i < arr.length; i++) {
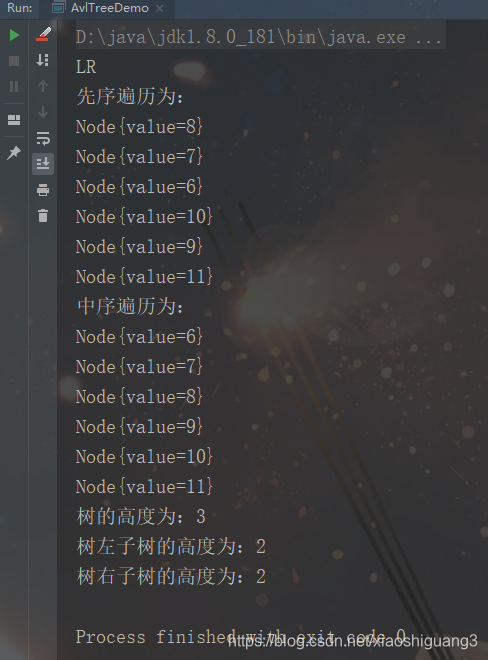
avlTree.add(new Node(arr[i]));
}
System.out.println("先序遍历为:");
avlTree.preOrder();
System.out.println("中序遍历为:");
avlTree.infixOrder();
System.out.println("树的高度为:" + avlTree.getRoot().height());
System.out.println("树左子树的高度为:" + avlTree.getRoot().left.height());
System.out.println("树右子树的高度为:" + avlTree.getRoot().right.height());
}
}
//创建一个平衡二叉树
class AvlTree{
Node root;
//添加结点
public void add(Node node){
if (root == null){
//如果根节点为null则直接添加到根节点
this.root = node;
}else {
this.root.add(node);
}
}
public Node getRoot(){
return root;
}
//先序遍历
public void preOrder(){
if(root == null){
System.out.println("二叉排序树为空,无法遍历");
return;
}
root.preOrder();
}
//中序遍历
public void infixOrder(){
if(this.root == null){
System.out.println("二叉排序树为空,无法遍历");
}else {
this.root.infixOrder();
}
}
//查找要删除的结点
public Node searche(int value){
if(root == null){
return null;
}else {
return root.search(value);
}
}
//查找要删除的结点的父节点
public Node searchParent(int value){
if(root == null){
return null;
}else {
return root.searchParent(value);
}
}
/**
* 删除已node为根节点的二叉排序树的的最小结点,并返回该最小结点的值
* @param node
* @return
*/
public int delRightTreeMin(Node node){
Node temp = node;
while (temp.left != null){
temp = temp.left;
}
//删除
delNode(temp.value);
return temp.value;
}
//删除结点
public void delNode(int value){
if(root == null){
return;
}else {
//先找到需要删除的结点
Node targetNode = searche(value);
//如果没有找打该节点则直接返回
if(targetNode == null){
return;
}
//如果当前二叉树只有一个节点
if(root.left == null && root.right == null){
//如果root结点就是要删除结点则直接将root置空
if(root.value == value){
root = null;
}
//否则直接返回
return;
}
//找到需要删除的结点的父节点
Node parent = searchParent(value);
//开始删除结点
if(targetNode.left == null && targetNode.right == null){ //要删除的结点是叶子结点
if(parent.left != null && parent.left.value == value){
//如果要删除的结点是父结点的左子树
parent.left = null;
}else if(parent.right != null && parent.right.value == value){
//如果要删除的结点是父结点的右子树
parent.right = null;
}
}else if(targetNode.left != null && targetNode.right != null){ //要删除的结点左子节点和右子节点都不为空
//先找到要删除结点的左子树的最小值并删除该最小值的结点
int minVal = delRightTreeMin(targetNode.right);
//将该最小值赋值给需要删除的结点
targetNode.value = minVal;
}else { //要删除的结点只有一颗子树
//如果要删除的结点有左子树
if(targetNode.left != null){
if(parent != null){
if(parent.left != null && parent.left.value == value){
parent.left = targetNode.left;
}else {
parent.right = targetNode.left;
}
}else {
root = targetNode.left;
}
}else {//如果要删除的结点有左子树
if(parent != null){
if(parent.left != null && parent.left.value == value){
parent.left = targetNode.right;
}else {
parent.right = targetNode.right;
}
}else {
root = targetNode.right;
}
}
}
}
}
}
//创建一个Node结点
class Node{
int value;
Node left;
Node right;
public Node(int value) {
this.value = value;
}
@Override
public String toString() {
return "Node{" +
"value=" + value +
'}';
}
//添加结点
public void add(Node node){
if(node == null){
return;
}
//比较需要添加的结点的值和当前结点的值的关系
if(node.value < this.value){
if(this.left == null){
//如果当前结点的左节点为null,则直接将需要添加的结点添加到该结点的左子树
this.left = node;
}else{
//递归添加向左添加该结点
this.left.add(node);
}
}else {
if(this.right == null){
//如果当前结点的右节点为null,则直接将需要添加的结点添加到该结点的左子树
this.right = node;
}else{
//递归添加向左添加该结点
this.right.add(node);
}
}
//如果添加完一个节点之后:(右子树的高度 - 左子树的高度) > 1,则进行左旋转(左旋转之前可能需要对右子结点进行右旋转),降低右子树的高度
if(rightHeight() - leftHeight() > 1){
//如果右子树的左子树高度 大于 右子树的右子树高度 则需要进行右旋转在进行左旋转
if(right != null && right.leftHeight() > right.rightHeight()){
//先对右子节点进行右旋转
right.rightRotate();
//在进行左旋转
leftRotate();
System.out.println("RL");
}else{
leftRotate();
}
return; //必须要()
}
//如果添加完一个结点之后:(左子树的高度 - 右子树的高度) > 1,则进行右旋转(右旋转之前可能需要对左子结点进行左旋转),降低左子树高度
if(leftHeight() - rightHeight() > 1){
//如果左子树的右子树高度 大于 左子树的左子树高度,则需要进行左旋转后在进行右旋转
if(left != null && left.rightHeight() > left.leftHeight()){
left.leftRotate();
rightRotate();
System.out.println("LR");
}else {
//直接进行右旋转
rightRotate();
}
}
}
//返回左子树的高度
public int leftHeight(){
if(left == null){
return 0;
}
return this.left.height();
}
//返回右子树的高度
public int rightHeight(){
if(right == null){
return 0;
}
return this.right.height();
}
//返回以当前结点为根节点的二叉树的高度
public int height(){
return Math.max(left == null ? 0 : left.height(), right == null ? 0 : right.height()) + 1;
}
//左旋转(降低右子树的高度)
public void leftRotate(){
//先创建一个新的结点,值为当前根节点的值
Node newNode = new Node(value);
//新的结点的左子树指向根节点的左子树
newNode.left = this.left;
//新节点的右子树指向根节点的右子树的左子树
newNode.right = this.right.left;
//将根节点的右子树的值赋值给根节点
this.value = this.right.value;
//根节点的右子树指向根节点的右子树的右子树
this.right = this.right.right;
//根节点的左子树指向新节点
this.left = newNode;
}
//右旋转(降低左子树的高度)
public void rightRotate(){
//创建一个新节点,值为根节点的值
Node newNode = new Node(value);
//新节点的右子树指向跟节点的左子树
newNode.right = right;
//新节点的左子树指向根节点的左子树的右子树
newNode.left = left.right;
//将根节点在值替换为左子节点的值
value = left.value;
//将当前结点的左子树设置为左子树的左子树
left = left.left;
//当前结点的右子树设置为新结点
right = newNode;
}
//先序遍历
public void preOrder(){
System.out.println(this);
if(this.left != null){
this.left.preOrder();
}
if(this.right != null){
this.right.preOrder();
}
}
//中序遍历
public void infixOrder(){
if(this.left != null){
this.left.infixOrder();
}
System.out.println(this);
if(this.right != null){
this.right.infixOrder();
}
}
//根据结点的value值查找结点
public Node search(int value) {
if(this.value == value){
return this;
}else if(this.value > value) {
if(this.left != null){
return this.left.search(value);
}else {
return null;
}
}else {
if(this.right != null){
return this.right.search(value);
}else {
return null;
}
}
}
//根据value查找该元素的父节点
public Node searchParent(int value) {
if((this.left != null && this.left.value == value) || (this.right != null && this.right.value == value)){
return this;
}else {
if(this.value > value && this.left != null){ //向左递归
return this.left.searchParent(value);
}else if(this.value < value && this.right != null){ //向右递归
return this.right.searchParent(value);
}else {
return null;
}
}
}
}
- 结果: