题目👇

- 编写求最大公因子的函数;
- 编写求模逆的扩展欧几里得算法函数;
- 编写rabin-miller素性检测算法函数;
- 编写生成大素数的算法函数;
- 编写生成RSA公私钥对的函数;
- 编写RSA加密和解密函数;
思路分析👇
1.这里传进两个参数,我的思路是从较小的数中倒序遍历出最大公因子。
倒序的原因是你一旦找到某个公因子,那么它一定是最大的公因子,可以节省时间。
另外还要对异常作出相应处理,如果参数中有0存在就返回-1,如果参数中有负数存在就将其转化成正数来处理。
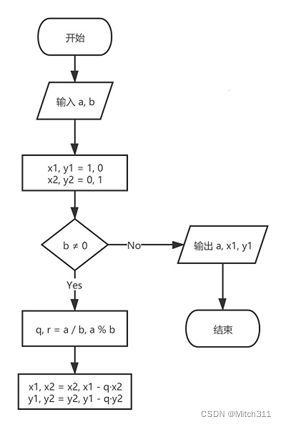
2.扩展欧几里得算法的具体步骤如下:
①若b≠0,使用带余除法,用b除以a得到余数r;否则转到第③步
②用b代替a,用r代替 b,重复第①步
③a的值就是最大公约数d
3.算法基于费马小定理,首先,根据Miller Rabin算法的过程:
假设需要判断的数是p,我们把p−1分解为2k∗t的形式;
当p是素数,有a2k∗t≡1(modp),然后随机选择一个数a,计算出at(mod p),让其不断的自乘,同时结合二次探测定理进行判断。
如果我们自乘后的数(modp)=1,但是之前的数(modp)≠±1,那么这个数就是合数(违背了二次探测定理)。
这样乘k次,最后得到的数就是ap−1,那么如果最后计算出的数不为1,这个数也是合数(费马小定理)。
4.生成指定比特位大小的随机数,利用刚才设计的Miller-Rabin算法来检验是否是素数,如果不是素数还需要重新生成一个随机数,如果是素数就返回即可。
5.过程如下:
①选取两个随机的指定比特位大小的素数p,q,这一步自然是由上一个RandomPrime()函数来生成。
②计算二者乘积 n=pq。
③随机选取选取参数e,并且测试是否满足(e,(p-1)(q-1))=1,不满足重新选取e,如满足则计算d满足ed+x(p-1)(q-1)=1,这一步使用扩展欧几里得算法来实现。
6.①RSA的加密过程可以使用一个通式来表达
密文=明文^e mod n
也就是说RSA加密是对明文的e次方后除以n后求余数的过程。
从通式可知,只要知道e和n任何人都可以进行RSA加密了,所以说e、n是RSA加密的密钥,也就是说e和n的组合就是公钥,所以我们就用(e,n)来表示公钥=(e,n)
②RSA解密过程也可以使用一个通式来表达,类似加密
明文 = 密文^d mod n
也就是说对密文进行d次方后除以n的余数就是明文,这就是RSA解密过程。知道d和n就能进行解密密文了,所以d和n的组合就是私钥=(d,n)
代码示例👇
#coding:utf-8
#author:Mitchell
#date:12.10
#利用math和random模块实现RSA加密算法
import numpy as np
import random
import math
#(1)编写求最大公因子的函数
def gcd(a,b):
if a!=0 and b!=0:
#将负数转化为正数
if a<0:
a=-a
if b<0:
b=-b
#从较小的数中倒序遍历出最大公因子
if a>b:
#倒序寻找最大公因子
for i in range(b,0,-1):
if a%i==0 and b%i==0:
return i
elif a==b:
return a
else:
#倒序寻找最大公因子
for i in range(a,0,-1):
if a%i==0 and b%i==0:
return i
else:
return -1
print('gcd(144,96)=',gcd(144,96))
#(2)编写求模逆的扩展欧几里得算法函数;
def EXgcd(a,b,x=[1],y=[1]):
if b==0:
x[0]=1
y[0]=0
return a
gcd=EXgcd(b,a%b,x,y)
k=int(a/b)
temp=x[0]
x[0]=y[0]
y[0]=temp-k*y[0]
return gcd
x=[0]
y=[0]
print('EXgcd(15,6)=',EXgcd(15,6,x,y))
print('x=',x,'y=',y)
#(3)编写rabin-miller素性检测算法函数;
def MillerRabin(n):
if n in {2,3,5,7,11,13}:
return True
elif n==1 or n%2==0 or n%3==0 or n%5==0 or n%7==0 or n%11==0 or n%13==0:
return False
k=0#判断向右移动位数
d=n-1#对u分解
while d%2==0:
k+=1
d/=2
m=d
a=random.randint(2,n-1)
r=pow(a,int(m),int(n))#r=a**m%n
if r==1:
return True
else:
for i in range(k):
if r==n-1:#r%n==-1
return True
else:
r=pow(r,2,n)
return False
print('MillerRabin(23)=',MillerRabin(23))
print('MillerRabin(97)=',MillerRabin(97))
print('MillerRabin(1024)=',MillerRabin(1024))
print('MillerRabin(1023)=',MillerRabin(1023))
#(4)编写生成大素数的算法函数;
def RandomPrime(length):#参数为比特位长度
n=random.randint(2**(length-1),2**length)
while(not MillerRabin(n)):
n=random.randint(2**(length-1),2**length)
return n
print('RandomPrime(4)=',RandomPrime(4))
print('RandomPrime(16)=',RandomPrime(16))
print('RandomPrime(64)=',RandomPrime(64))
#(5)编写生成RSA公私钥对的函数;
def GetKey(length):#参数是比特位长度
#生成两个指定大小的素数
p=RandomPrime(length)
q=RandomPrime(length)
#print('p=',p,'q=',q)
n=p*q
#生成公钥e
e=RandomPrime(random.randint(10,length%20+11))
#保证e与(p-1)*(q-1)互素,便于使用扩展欧几里得求其逆
while gcd(e,(p-1)*(q-1))!=1 or e>=(p-1)*(q-1):
e=RandomPrime(random.randint(10,length%20+11))
#利用扩展欧几里得求逆,d即为私钥
d=[0]
d_=[0]
temp=EXgcd((p-1)*(q-1),e,d_,d)
#函数返回n,公钥e和私钥d构成的列表
return [n,e,d[0]]
length=int(input('请输入测试数据的比特位长度:'))
key=GetKey(length)
print('n=',key[0],'公钥e=',key[1],'私钥d=',key[2])
#(6)编写RSA加密和解密函数
def enCrypto(plainText,n,e):
return pow(plainText,e,n)
def deCrypto(cryptoText,n,d):
return pow(cryptoText,d,n)
#测试,生成随机明文
plainText=random.randint(2**(length-1),2**length)
print('plainText=',plainText)
print('加密结果=',enCrypto(plainText,key[0],key[1]))
print('解密结果=',deCrypto(enCrypto(plainText,key[0],key[1]),key[0],key[2]))
