一、0-1背包
1.1、0-1背包解决的问题
给你 i 个物品,每个物品都具有两个属性(价值value[ i ]和重量weight[ i ]),将他们放入容量为 j 的背包中(不可以重复放入同一个物品),怎么放才能让背包的价值最大?
1.2、dp数组定义
一维和二维都可以这样定义:
dp[ i ][ j ] 或 dp[ j ]:从前i个物品中任选,装满容量为j的背包的最大价值;
1.3、转移方程
转移方程:
二维:dp[ i ][ j ] = Math.max( dp[ i - 1 ][ j ], dp[ i - 1 ][ j - weight[ i ] ] + value[ i ] ) ;
一维(状态压缩,优化):dp[ j ] = Math.max( dp[ j ], dp[ j - weight[ i ] + value[ i ]] );
怎么得出来的???
1.3.1、二维dp数组
注意:如果看不懂了,多往上看看dp数组的定义~
dp[ i ][ j ]这个状态,就是由上一个状态得来,怎么得来?一种是不放第 i 个物品( dp[ i - 1 ][ j ] ),一种是放第 i 个物品 (dp[ i - 1 ][ j - weight[ i ] ] + value[ i ]);
不放第 i 个物品的理解:
不放第 i 个物品好理解,无非就是上一个状态,物品还是i - 1个物品,容量还是 j;
放第 i 个物品的理解:
可以理解为这么一个过程:(按顺序往下走)
1、[ i - 1 ],这个时候,还没有放入第i个物品,所以这个时候背包里只有装物品 i 之前的所有物品;
2、[ j - weight[ i ] ],因为要放物品i,所以要在背包中,给物品 i 预留一个空间,减掉 weight[ i ] 就表示已经给物品 i 腾出空间了,那么接下来就要放入了;
3、+ value[ i ],就表示放入第 i 个物品,那么这个背包里面的价值要增加第 i 个物品的价值;
1.3.2、一维dp数组
仔细观察,通过对比,你就会发现,二维和一维的dp数组只是少了 i 这个维度,转移方程的形式是没有变的;
为什么能这样压缩成一维dp数组?
因为一维dp数组实际上对二维矩阵每一层的一个拷贝,例如,遍历到二维矩阵的第三层时,一维dp数组就直接将第二层的数据拷贝过来直接用,以此类推;
值得注意是:压缩成一维以后,遍历背包大小时,要逆序遍历背包的大小(从大到小遍历),原因如下图:
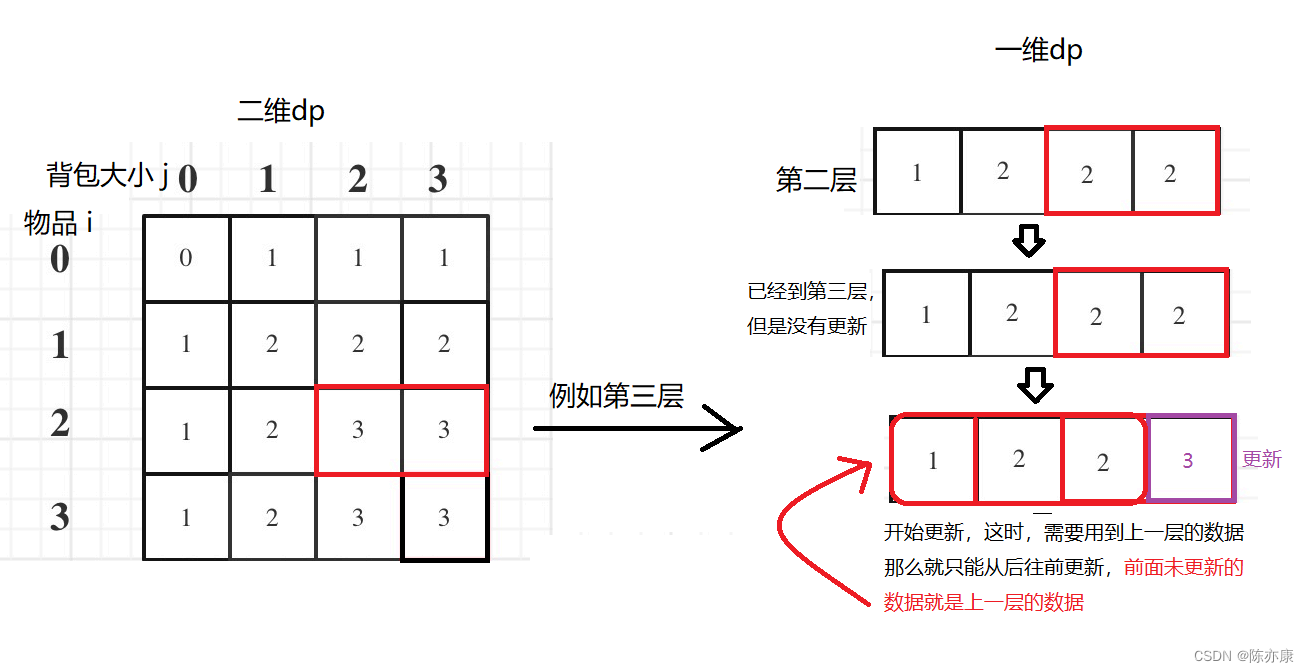
1.4、遍历顺序
对于二维dp数组(未压缩)而言:
先遍历物品,再遍历背包
或者
先遍历背包,再遍历物品
都可以!
并且
初始化好之后,顺序和逆序遍历背包大小都可以!
对于一维dp数组(压缩)而言:
先遍历物品,再遍历背包
或者
先遍历背包,再遍历物品
都可以!
但是
初始化好之后,只能逆序遍历背包,原因如下:

1.5、测试代码
二维dp:
//0-1背包 二维测试代码
/**
* @param weight 物品重量
* @param value 物品价值
* @param maxWeight 背包最大容量
* @return
*/
public int dynamic1(int[] weight, int[] value, int maxWeight) {
int len = weight.length;//物品数量
int[][] dp = new int[len][maxWeight + 1];
//初始化
for(int i = 0; i <= maxWeight; i++) {
if(i >= weight[0]) {
dp[0][i] = value[0];
}
}
for(int i = 1; i < len; i++) { //物品
for(int j = 0; j <= maxWeight; j++) { //容量
if(j < weight[i]) {
dp[i][j] = dp[i - 1][j];
} else {
dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
}
}
}
return dp[len - 1][maxWeight];
}
public static void main(String[] args) {
Test3 test3 = new Test3();
int[] weight = {1, 3, 4};
int[] value = {15, 20, 30};
test3.dynamic1(weight, value, 4);
}
一维dp:
/**
* 0-1背包 一维测试
* @param weight 物品重量
* @param value 物品价值
* @param maxWeight 背包最大容量
* @return
*/
public int dynamic2(int[] weight, int[] value, int maxWeight) {
int len = weight.length;//物品数量
int[] dp = new int[maxWeight + 1];
//初始化
for(int i = 0; i < len; i++) { //物品
for(int j = maxWeight; j >= weight[i]; j--) {
dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);
}
}
return dp[maxWeight];
}
public static void main(String[] args) {
Test3 test3 = new Test3();
int[] weight = {1, 3, 4};
int[] value = {15, 20, 30};
test3.dynamic2(weight, value, 4);
}
1.6、练习
建议三刷:
416. 分割等和子集
1049. 最后一块石头的重量 II
494. 目标和
474. 一和零
二、完全背包
2.1、完全背包解决问题
给你 i 个物品,每个物品都具有两个属性(价值value[ i ]和重量weight[ i ]),将他们放入容量为 j 的背包中(可以重复放入同一个物品),怎么放才能让背包的价值最大?
2.2、与0-1背包的区别
1. 在转移方程上,几乎没有差别;
2. 在定义dp数组上,一个是可以重复取物品,一个不可以重复取物品;
3. 对于问题“装满背包,有几种方法”这个问题上,遍历顺序上(先遍历背包还是物品?),很有考究,后文有详细讲到
4. 背包容量的遍历顺序上,无论是二维还是一维,都和0-1背包是相反的;
总的来讲,0-1背包装物品,是不可以重复装同一个物品,而完全背包,是可以重复装一个物品;
Ps:在完全背包的问题中,建议直接使用一维的dp数组,好理解,也省去了很多不必要的步骤
2.3、测试代码
二维dp:
/**
* 完全背包 二维测试代码
* @param weight 物品重量
* @param value 物品价值
* @param maxWeight 背包最大容量
* @return
*/
public int dynamic(int[] weight, int[] value, int maxWeight) {
int len = weight.length;//物品数量
int[][] dp = new int[len][maxWeight + 1];
//初始化
for(int i = weight[0]; i <= maxWeight; i++) {
dp[0][i] = dp[0][i - 1] + value[0];
}
for(int i = 1; i < len; i++) { //物品
for(int j = maxWeight; j >= 0; j--) {
if(j < weight[i]) {
dp[i][j] = dp[i - 1][j];
} else {
dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
}
}
}
return dp[len - 1][maxWeight];
}
public static void main(String[] args) {
Test3 test3 = new Test3();
int[] weight = {1, 3, 4};
int[] value = {15, 20, 30};
test3.dynamic2(weight, value, 4);
}
一维dp:
/**
* 完全背包 一维测试代码
* @param weight 物品重量
* @param value 物品价值
* @param maxWeight 背包最大容量
* @return
*/
public int dynamic4(int[] weight, int[] value, int maxWeight) {
int len = weight.length;//物品数量
int[] dp = new int[maxWeight + 1];
//初始化
for(int i = 0; i < len; i++) { //物品
for(int j = weight[i]; j <= maxWeight; j++) { //背包
dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);
}
}
return dp[maxWeight];
}
public static void main(String[] args) {
Test3 test3 = new Test3();
int[] weight = {1, 3, 4};
int[] value = {15, 20, 30};
test3.dynamic4(weight, value, 4);
}
2.4、拓展问题:装满背包有几种方法?
这是一个拓展的问题,问题就是:装满背包有几种方法?
对于这类问题通解:
dp定义:从前 i 个商品中任取,装满容量为 j 的背包,有dp[ i ]种方法;
dp方程:dp[ j ] = dp[ j ] + dp[ j - weight[ i ] ];
怎么理解?
不用想太复杂,当前背包装满的方法,就两种情况,一种是装第 i 个物品,一种是不装第 i 个物品;
求当前背包装满的方法数,就是装与不装第 i 个商品方法的总和;(这里的不装即使指,不装第 i 个物品,通过装满之前背包的方法(物品)来装满背包,所以就是dp[ j ],用的方法一样,所以不变);
2.5、排列与组合
上文中提到,完全背包在“装满背包,有几种方法”这个问题上,“先遍历背包还是先遍历物品?”十分有讲究,那么这个顺序有什么区别呢?往下看
2.5.1、组合
//组合
for(int i = 0; i < len; i++) { //物品
for(int j = weight[i]; j <= maxWeight; j++) { //背包
dp[i] = dp[i] + dp[i - weight[j]];
}
}
先遍历物品再遍历背包,得到的就是一个组合数,也就是说,不需要考虑顺序;例如得到的方法中,一组数是[1, 3, 4],那么就不可能出现另一组数据为[3, 1, 4];
先遍历物品再遍历背包,就出现了以上情况,为什么?
因为我们每次是拿到物品1,然后遍历一次背包,拿到物品2,再遍历一次背包......
你就可以发现他是一个有序的过程,不会出现先拿物品2,再拿物品1的情况!
更通俗来讲: 先遍历物品的时候相当于是先把这个物品放进去了然后再看其他的能不能放进去,所以不会出现逆序。
2.5.2、排列
//排列
for(int j = 0; j <= maxWeight; j++) { //背包
for(int i = 0; i < len; i++) { //物品
if(i >= weight[j]) {
dp[i] = dp[i] + dp[i - weight[j]];
}
}
}
先遍历背包再遍历物品,得到的就是一个排列数,需要考虑顺序,例如得到的方法中,一组数是[1, 3, 4],那么就需要考虑出现另一组数据为[3, 1, 4]的情况;
先遍历背包再遍历物品,就出现了以上情况,为什么?
当背包的容量为1时,就遍历一次物品,容量为2时,就遍历一次物品......
因为物品排序和其重量排序不一致,所以先遍历背包不仅会出现1,2的情况,还会出现2,1这种情况;
更通俗来讲:先遍历背包相当于是用每个大小的背包看看把每一个物品都放进去一次再看别的物品能不能放进去,所以可以有逆序。
2.6、练习
建议三刷:
518. 零钱兑换 II
377. 组合总和 Ⅳ
322. 零钱兑换
279. 完全平方数
139. 单词拆分

