斐波那契数列（Fibonacci sequence）是一个经典的数学问题，数列中的每一项是前两项之和。它的递归定义如下：

• F(0)=0
• F(1)=1
• F(n)=F(n−1)+F(n−2)（当 n>1）

接下来，逐步深度讲解它的实现方式及其背后的原理。

---

一、递归实现

代码

def fibonacci_recursive(n):
    if n == 0:
        return 0
    elif n == 1:
        return 1
    else:
        return fibonacci_recursive(n - 1) + fibonacci_recursive(n - 2)

# 示例
n = 10
print([fibonacci_recursive(i) for i in range(n)])

原理分析

1. 递归调用：

   • 函数 fibonacci_recursive 会递归计算 F(n−1) 和 F(n−2)
   • 每次递归都拆分成两个子问题，直到遇到基准情况F(0) 和 F(1)。

2. 效率问题：

   • 时间复杂度是 O(2^n)，因为每个 F(n) 都重复计算了大量 F(k) 的值。
   • 空间复杂度是 O(n)，因为递归深度最大为 n。

---

 

二、带缓存的递归（记忆化）

代码

from functools import lru_cache

@lru_cache(maxsize=None)
def fibonacci_memoized(n):
    if n == 0:
        return 0
    elif n == 1:
        return 1
    else:
        return fibonacci_memoized(n - 1) + fibonacci_memoized(n - 2)

# 示例
n = 10
print([fibonacci_memoized(i) for i in range(n)])

 

原理分析

1. 缓存：

   • lru_cache 会自动存储已计算的结果。
   • 每次递归调用时，先检查缓存，如果存在结果，就直接返回。

2. 效率改进：

   • 时间复杂度降为 O(n)，因为每个 F(k) 只计算一次。
   • 空间复杂度仍然是 O(n)，用于存储缓存。

---

三、动态规划

代码

def fibonacci_dp(n):
    if n == 0:
        return 0
    elif n == 1:
        return 1
    
    dp = [0, 1]
    for i in range(2, n + 1):
        dp.append(dp[-1] + dp[-2])
    return dp[-1]

# 示例
n = 10
print([fibonacci_dp(i) for i in range(n)])

 

原理分析

1. 状态转移方程：

   • F(n)=F(n−1)+F(n−2)
   • 通过一个数组 dp[] 存储中间结果，避免重复计算。

2. 效率：

   • 时间复杂度是 O(n)，每个 F(k) 只计算一次。
   • 空间复杂度是 O(n)（存储数组大小）。

---

 

四、动态规划优化（滚动数组）

代码

def fibonacci_optimized(n):
    if n == 0:
        return 0
    elif n == 1:
        return 1
    
    prev, curr = 0, 1
    for _ in range(2, n + 1):
        prev, curr = curr, prev + curr
    return curr

# 示例
n = 10
print([fibonacci_optimized(i) for i in range(n)])

 

原理分析

1. 空间优化：

   • 只保留两个变量 prev 和 curr 表示前两项，消除数组存储。

2. 效率：

   • 时间复杂度仍为 O(n)。
   • 空间复杂度降为 O(1)。

---

五、矩阵快速幂法

代码

import numpy as np

def fibonacci_matrix(n):
    if n == 0:
        return 0
    
    F = np.array([[1, 1], [1, 0]], dtype=object)
    result = np.linalg.matrix_power(F, n - 1)
    return result[0, 0]

# 示例
n = 10
print([fibonacci_matrix(i) for i in range(n)])

原理分析

1. 数学公式：

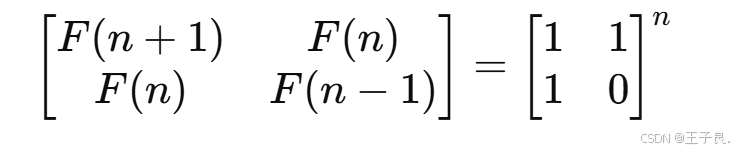
   • 斐波那契数列可以表示为矩阵幂： 

时间复杂度是 O( log⁡ n)，利用矩阵快速幂计算。