原题：数字三角形（递推、简单DP）

原题链接：[USACO1.5][IOI1994]数字三角形 Number Triangles - 洛谷

题目描述： 

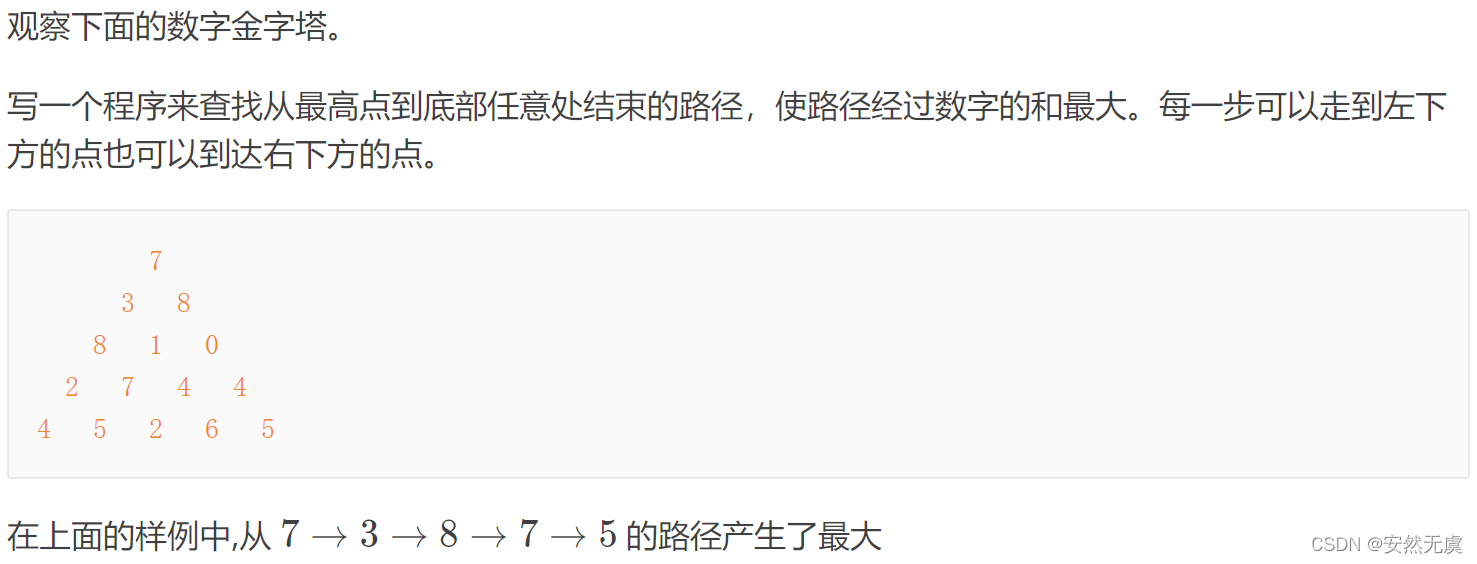
输入格式：

第一个行一个正整数 n ,表示行的数目。

后面每行为这个数字金字塔特定行包含的整数。

输出格式：

单独的一行,包含那个可能得到的最大的和。

数据范围：

1 ≤ n ≤ 1000，三角形数字值在 [0,100] 范围内。 

示例:

输入：

5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5 

输出：

30

思路：

本题采用倒推的方式：

假设func[i][j]表示的是从 i, j 到最后一层的最大路径之和

当从顶层沿某条路径走到第i层向第i+1层前进时，我们的选择是沿其下两条可行路径中最大数字的方向前进，所以找出递推关系：func[i][j] += max(func[i+1][j],func[i+1][j+1])；
注意：func[i][j]表示当前数字的值，func[i+1][j]和func[i+1][j+1]分别表示从i+1,j、i+1,j+1到最后一层的最大路径之和；
最终func[0][0]就是所求

代码执行：

#include<stdio.h>
#include<algorithm>
using namespace std;

int func[1005][1005] = {0};

int main()
{
    int n = 0;
    scanf("%d", &n);
    int i = 0;
    int j = 0;
    for(i = 0; i < n; i++)
    {
        for(j = 0; j <= i; j++)
        {
            scanf("%d", &func[i][j]);
        }
    }
    //假设func[i][j]表示的是从i, j到最后一层的最大路径之和
    //找出递推关系：func[i][j]+=max(func[i+1][j],func[i+1][j+1]);
    //func[i][j]表示当前数字的值，func[i+1][j]和func[i+1][j+1]分别表示从i+1,j、i+1,j+1到最后一层的最大路径之和
    //最终func[0][0]就是所求
    for(i = n - 2; i >= 0; i--)
    {
        for(j = 0; j <= i; j++)
        {
            func[i][j] += max(func[i+1][j], func[i+1][j+1]);
        }
    }
    printf("%d\n", func[0][0]);
    return 0;