一、图的基本概念及相关名词解释
1.1 图的基本概念
图是比线性表和树更为复杂且抽象的结，和以往所学结构不同的是图是一种表示型的结构，也就是说他更关注的是元素与元素之间的关系。下面进入正题。
图是由顶点集合及顶点间的关系组成的一种数据结构：G（Graph） = (V， E)，其中：
（1）顶点集合V(Vertex) = {x|x属于某个数据对象集}是有穷非空集合；
（2）E（Edge） = {(x,y)|x,y属于V}或者E = {<x, y>|x,y属于V && Path(x, y)}是顶点间关系的有穷集合，也叫做边的集合。其中 (x, y)表示x到y的一条双向通路，即(x, y)是无方向的；Path(x, y)表示从x到y的一条单向通路，即Path(x, y)是有方向的。（也就是说图分为有向和无向）
下面我们通过一些图来了解一些相关的名词
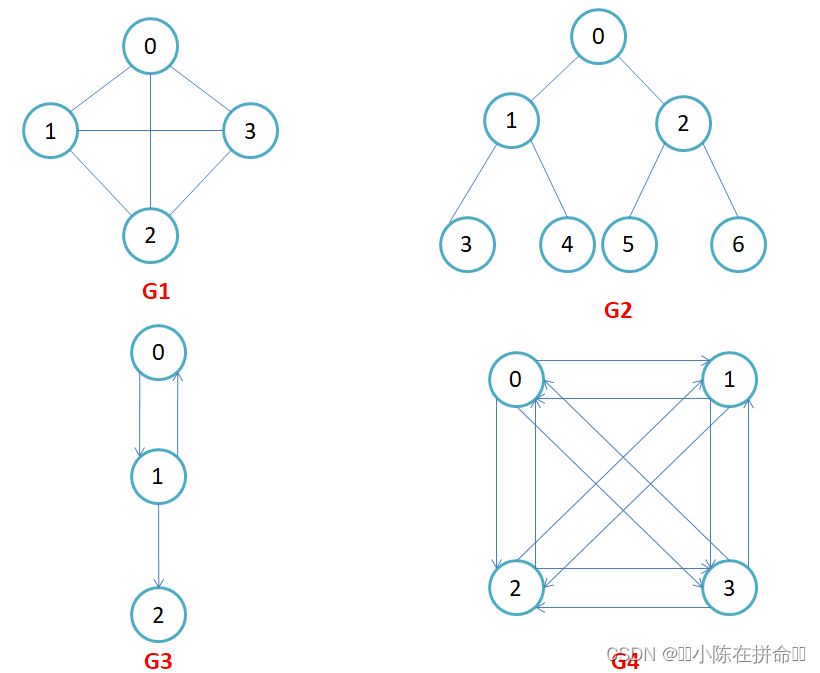
在介绍相关名词之前，大家有没有发现G2和我们的二叉树是一样的？那么图和二叉树究竟有什么关系呢？？
其实本质上来说，树是一种特殊的无环连通图，图不一定是树。另一方面，树关注的是节点中存的值，而图关注的是顶点和边的权值（边附带的数据信息）
1.2 图的相关名词解释
顶点和边：图中结点称为顶点，第i个顶点记作vi。两个顶点vi和vj相关联称作顶点vi和顶点vj之间有一条边，图中的第k条边记作ek，ek = (vi，vj)或<vi，vj>
有向图和无向图（边是否有方向）：在有向图中，顶点对<x, y>是有序的，顶点对<x，y>称为顶点x到顶点y的一条边(弧)，<x, y>和<y, x>是两条不同的边，比如上图G3和G4为有向图。在无向图中，顶点对(x, y)是无序的，顶点对(x,y)称为顶点x和顶点y相关联的一条边，这条边没有特定方向，(x, y)和(y，x)是同一条边，比如上图G1和G2为无向图。注意：无向边(x, y)等于有向边<x, y>和<y, x>
完全图（即每一个顶点都和其他顶点有边）：在有n个顶点的无向图中，若有n * (n-1)/2条边，即任意两个顶点之间有且仅有一条边，则称此图为无向完全图，比如上图G1；在n个顶点的有向图中，若有n * (n-1)条边，即任意两个顶点之间有且仅有方向相反的边，则称此图为有向完全图，比如上图G4。
邻接顶点（通过边关联起来的两个点）：在无向图中G中，若(u, v)是E(G)中的一条边，则称u和v互为邻接顶点，并称边(u,v)依附于顶点u和v；在有向图G中，若<u, v>是E(G)中的一条边，则称顶点u邻接到v，顶点v邻接自顶点u，并称边<u, v>与顶点u和顶点v相关联。
顶点的度（有几条边就有多少度）：顶点v的度是指与它相关联的边的条数，记作deg(v)。在有向图中，顶点的度等于该顶点的入度与出度之和，其中顶点v的入度是以v为终点的有向边的条数，记作indev(v);顶点v的出度是以v为起始点的有向边的条数，记作outdev(v)。因此：dev(v) = indev(v) + outdev(v)。注意：对于无向图，顶点的度等于该顶点的入度和出度，即dev(v) = indev(v) = outdev(v)。
路径：在图G = (V， E)中，若从顶点vi出发有一组边使其可到达顶点vj，则称顶点vi到顶点vj的顶
点序列为从顶点vi到顶点vj的路径。
路径长度：对于不带权的图，一条路径的路径长度是指该路径上的边的条数；对于带权的图，一
条路径的路径长度是指该路径上各个边权值的总和。
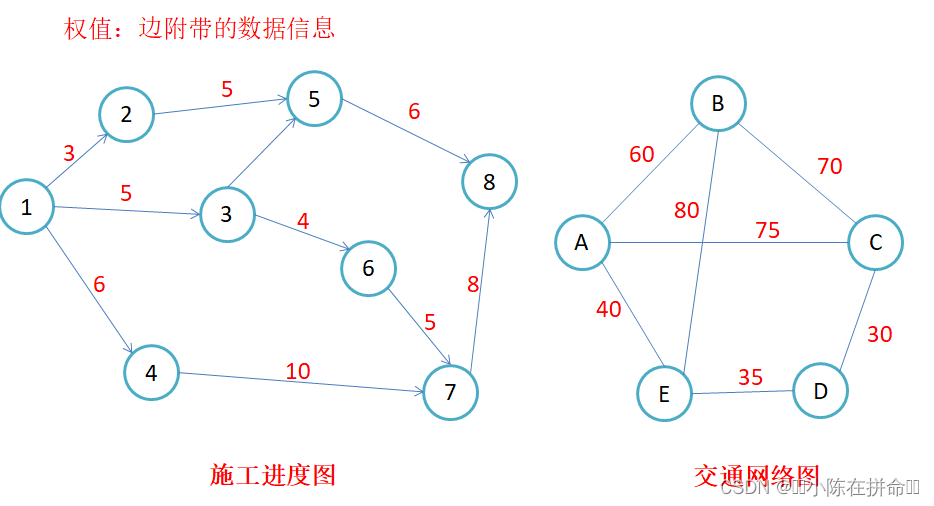
权值：边附带的数据信息
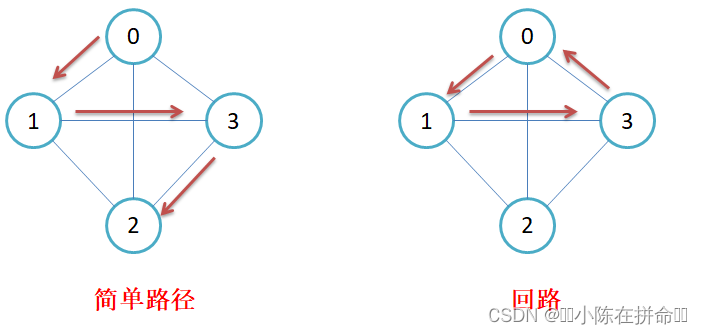
简单路径与回路：若路径上各顶点v1，v2，v3，…，vm均不重复，则称这样的路径为简单路
径。若路径上第一个顶点v1和最后一个顶点vm重合，则称这样的路径为回路或环。
子图（顶点和边都是原图的一部分）：设图G = {V, E}和图G1 = {V1，E1}，若V1属于V且E1属于E，则称G1是G的子图。
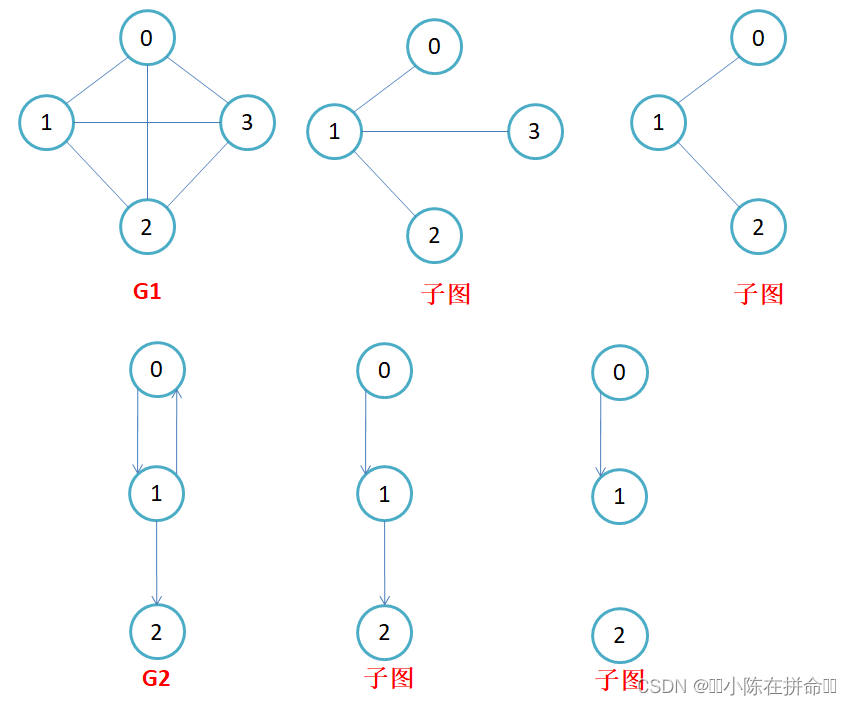
连通图（无向图）：在无向图中，若从顶点v1到顶点v2有路径，则称顶点v1与顶点v2是连通的。如果图中任意一对顶点都是连通的，则称此图为连通图。
强连通图（有向图）：在有向图中，若在每一对顶点vi和vj之间都存在一条从vi到vj的路径，也存在一条从vj到vi的路径，则称此图是强连通图
生成树（无向图）：一个连通图的最小连通子图称作该图的生成树。有n个顶点的连通图的生成树有n个顶点和n-1条边。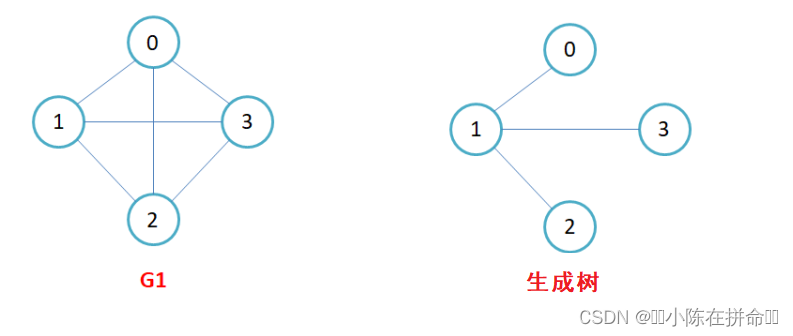
最小生成树（无向图）：生成树中边的权值最小的生成树 ，所谓最小是指边的权值之和小于或者等于其它生成树的边的权值之和。 （后面会介绍最小生成树的相关算法）
1.3 图的一些现实应用
1.3.1 保证连通情况下修路的最小开销（最小生成树）
用最小的代价连通起来。
1.3.2 社交关系
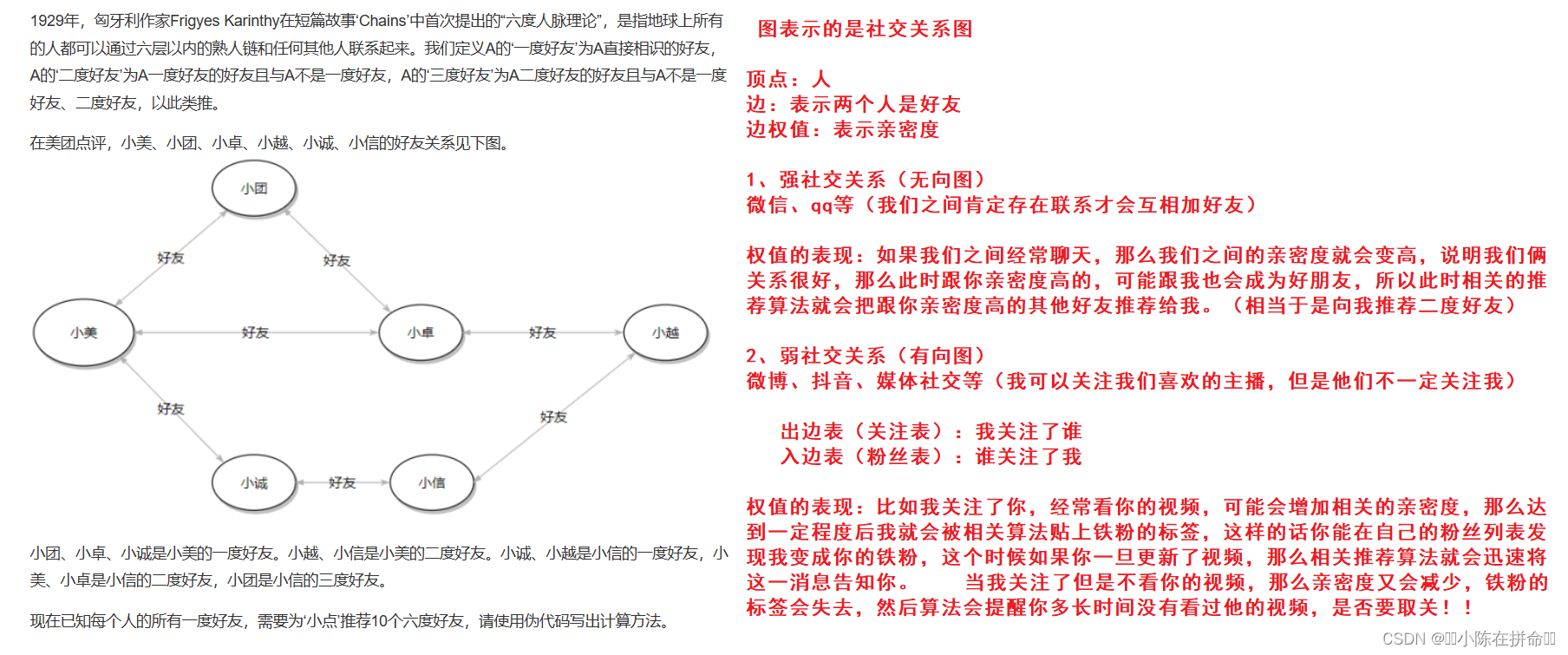
二、图的存储结构
因为图中既有节点，又有边(节点与节点之间的关系)，因此，在图的存储中，只需要保存：节点和边关系即可。节点保存比较简单，只需要一段连续空间即可，那么通过对关系的保存，从而衍生除了以下两种存储结构——邻接矩阵和邻接表。
2.1 邻接矩阵
因为节点与节点之间的关系就是连通与否，即为0或者1，因此邻接矩阵(二维数组)即是：先用一个数组将定点保存，然后采用矩阵来表示节点与节点之间的关系。
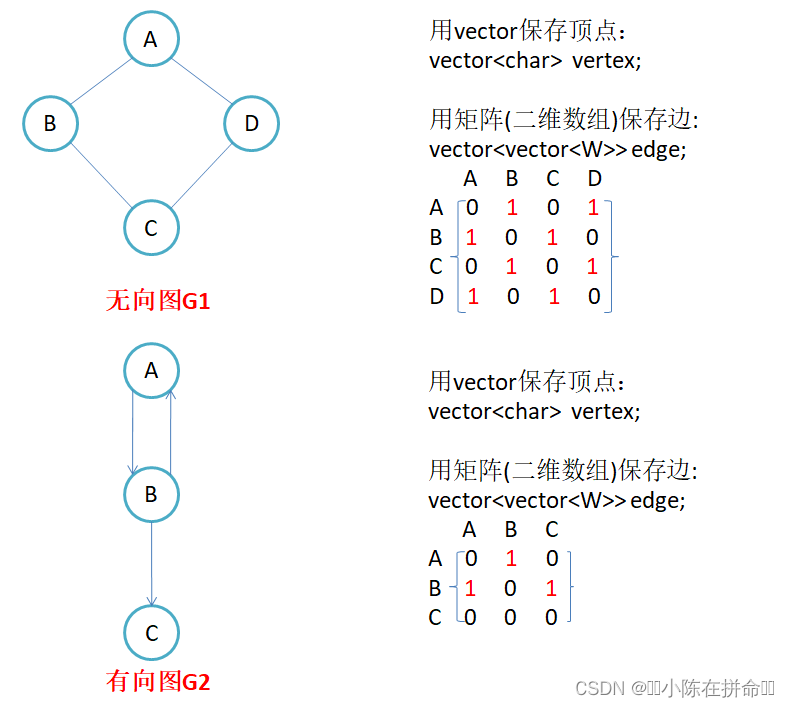
注意：
1. 无向图的邻接矩阵是对称的，第i行(列)元素之和，就是顶点i的度。有向图的邻接矩阵则不一定是对称的，第i行(列)元素之后就是顶点i 的出(入)度（一般来说存的是出度）。
2. 如果边带有权值，并且两个节点之间是连通的，上图中的边的关系就用权值代替，如果两个
顶点不通，则使用无穷大（用一个基本上不可能出现的权重）代替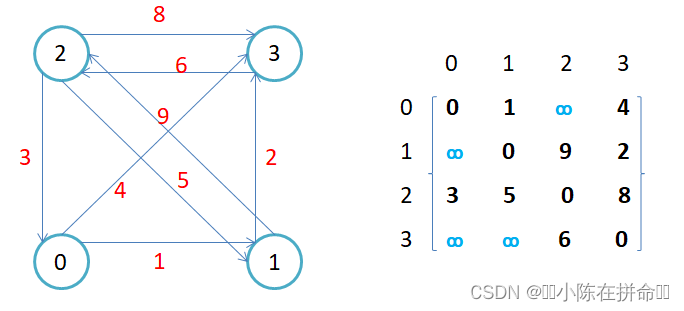
3. 用邻接矩阵存储图的优点是能够快速知道两个顶点是否连通O(1)，缺陷是如果顶点比较多，边比
较少时，比较浪费空间，并且（1）要求两个节点之间的路径不是很好求（2）不适合查找一个顶点连接的所有边O（N）
2.2 邻接矩阵的简单模拟实现
图创建的方式:
1、io输入 不方便测试 再oj中较为合适
2、图结构关系写到文件，读取文件
3、手动去添加边，这样会更方便测试！！
结构：
_vertexs 顶点集合
map<V, size_t> _IndexMap; 顶点和下标的映射 方便通过顶点快速找到下标 然后在邻接矩阵中O（1）拿到权值
vector<vector<W>> _matrix; // 存储边集合以及对应权值的邻接矩阵
namespace Matrix //以邻接矩阵的形式封装
{
template<class V, class W, W MAX_W = INT_MAX, bool Direction = false> //V表示顶点 W表示权重 MAX_W表示默认的权重值 Direction表示是有向图还是无向图 后面两个是非类型模版参数(缺省)
class Graph
{
typedef Graph<V, W, MAX_W, Direction> Self;
public:
//图创建的方式
//1、io输入 不方便测试 再oj中较为合适
//2、图结构关系写到文件，读取文件
//3、手动去添加边，这样会更方便测试！！
Graph() = default; //强制生成默认构造
Graph(const V* vertexs, size_t n) //传一个顶点相关的集合进行初始化
{
_vertexs.reserve(n);
for (size_t i = 0; i < n; ++i) //初始化顶点集合
{
_vertexs.push_back(vertexs[i]);//存到顶点集合里
_IndexMap[vertexs[i]] = i;//建立顶点和下标的映射关系，方便我们进行查找
}
//初始化邻接矩阵
_matrix.resize(n);
for (auto& e : _matrix) e.resize(n, MAX_W);
}
//获取顶点的下标(为什么要单独给这样一个函数呢？因为可能给的是一个错误的顶点，要检查一下)
size_t GetVertexIndex(const V& v)
{
//有可能顶点会给错，这样在map中就找不到 所以要先检查一下
auto it = _IndexMap.find(v);
if (it != _IndexMap.end()) return it->second;
else
{
throw invalid_argument("不存在的顶点");//抛异常(异常被捕获后可以不做处理)
//断言太暴力了，会直接终止程序，并且断言在release版本下会被屏蔽
//异常被捕获后可以不作处理，程序从捕获位置继续执行。 而断言是完全无法忽略的，程序在断言失败处立即终止。
// 因此断言通常用于调试版本，用来发现程序中的逻辑错误。 虽然异常也能起到这样的作用，但是不应该用异常代替断言：
// 1) 如果发现了逻辑错误，必须修改程序，而不可能在程序中进行处理和恢复，所以不需要向外传送，没有必要使用异常。
// 2) 使用断言的开销比异常小得多，而且断言可以从发布版中完全去除。
return -1; //还是要返回，因为编译器不会在乎运行，而是会检查你在这边有没有返回
}
}
//利用序号为两个节点添加边
void _AddEdge(size_t srci, size_t dsti, const W& w)
{
_matrix[srci][dsti] = w;
//如果是无向图
if (Direction == false) _matrix[dsti][srci] = w;
}
//对两个节点添加边，以及权重关系 src代表起点 dst代表中点 w代表权重
void AddEdge(const V& src, const V& dst, const W& w)
{
size_t srci = GetVertexIndex(src);
size_t dsti = GetVertexIndex(dst);
_AddEdge(srci, dsti, w);
}
void Print()//帮助我们测试
{
//顶点
for (size_t i = 0; i < _vertexs.size(); ++i)
cout << "[" << i << "]" << "->" << _vertexs[i] << endl; //下标映射顶点集合
cout << endl;
//打印横一行的下标
cout << " ";
for (size_t i = 0; i < _vertexs.size(); ++i) cout << i << " ";
cout << endl;
//打印矩阵
for (size_t i = 0; i < _matrix.size(); ++i)
{
cout << i << " ";
for (size_t j = 0; j < _matrix[i].size(); ++j)
if (_matrix[i][j] == MAX_W) cout << '*' << " ";
else cout << _matrix[i][j] << " ";
cout << endl;
}
cout << endl;
}
private:
map<V, size_t> _IndexMap; //建立顶点和下标之间的关系，方便我们根据顶点去找他的下标 比如两个顶点是否存在关系，就可以快速找到两个顶点的下标，然后去邻接矩阵看一下
vector<V> _vertexs; // 顶点集合
vector<vector<W>> _matrix; // 存储边集合的矩阵
};
}2.3 邻接表
邻接表：使用数组表示顶点的集合，使用链表表示边的关系
结构：
_vertexs 顶点集合
map<V, size_t> _IndexMap; 顶点和下标的映射 方便通过顶点快速找到下标
vector<Edge*> _linktable; // 存储边集合的邻接表
1. 无向图邻接表存储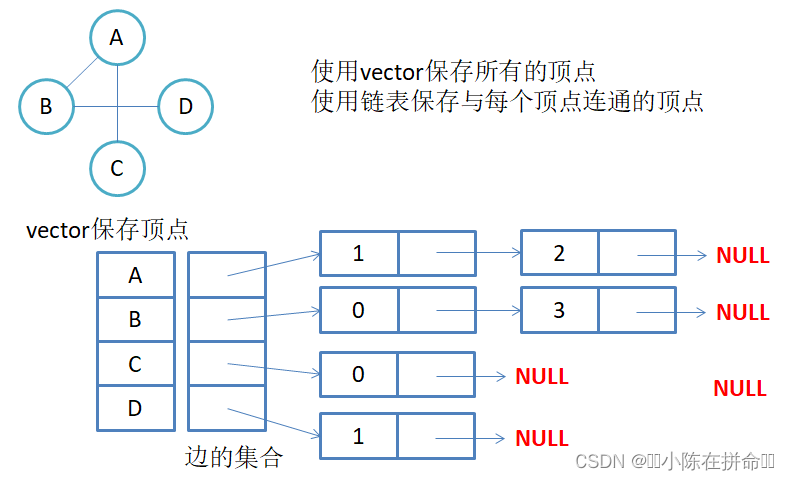
2.4 邻接表的简单模拟实现
namespace LinkTable //以邻接矩阵的形式封装
{
//实现一个边
template<class W> //边只要存权重即可
struct Edge
{
size_t _srci;//入边
size_t _dsti;//出边
W _w;//权重
Edge<W>* _next;//存下一个边
Edge(size_t srci ,size_t dsti, const W& w)
:_srci(srci)
,_dsti(dsti)
, _w(w)
, _next(nullptr)
{}
};
template<class V, class W, bool Direction = false> //V表示顶点 W表示权重 Direction表示是有向图还是无向图 后面两个是非类型模版参数(缺省)
class Graph
{
typedef Edge<W> Edge;
public:
//图创建的方式
//1、io输入 不方便测试 再oj中较为合适
//2、图结构关系写到文件，读取文件
//3、手动去添加边，这样会更方便测试！！
Graph(const V* vertexs, size_t n) //传一个顶点相关的集合进行初始化
{
_vertexs.reserve(n);
for (size_t i = 0; i < n; ++i) //初始化顶点集合
{
_vertexs.push_back(vertexs[i]);//存到顶点集合里
_IndexMap[vertexs[i]] = i;//建立顶点和下标的映射关系，方便我们进行查找
}
_linktable.resize(n, nullptr);//先初始化为空，后面手动去添加边
}
//获取顶点的下标(为什么要单独给这样一个函数呢？因为可能给的是一个错误的顶点，要检查一下)
size_t GetVertexIndex(const V& v)
{
//有可能顶点会给错，这样在map中就找不到 所以要先检查一下
auto it = _IndexMap.find(v);
if (it != _IndexMap.end()) return it->second;
else
{
throw invalid_argument("不存在的顶点");//抛异常(异常被捕获后可以不做处理)
//断言太暴力了，会直接终止程序，并且断言在release版本下会被屏蔽
//异常被捕获后可以不作处理，程序从捕获位置继续执行。 而断言是完全无法忽略的，程序在断言失败处立即终止。
// 因此断言通常用于调试版本，用来发现程序中的逻辑错误。 虽然异常也能起到这样的作用，但是不应该用异常代替断言：
// 1) 如果发现了逻辑错误，必须修改程序，而不可能在程序中进行处理和恢复，所以不需要向外传送，没有必要使用异常。
// 2) 使用断言的开销比异常小得多，而且断言可以从发布版中完全去除。
return -1; //还是要返回，因为编译器不会在乎运行，而是会检查你在这边有没有返回
}
}
void _AddEdge(size_t srci, size_t dsti, const W& w)
{
Edge* sd_eg = new Edge(srci, dsti, w);
//头插的逻辑
sd_eg->_next = _linktable[srci];
_linktable[srci] = sd_eg;
//如果是无向图 2->1
if (Direction == false)
{
Edge* ds_eg = new Edge(dsti,srci,w);
//头插的逻辑
ds_eg->_next = _linktable[dsti];
_linktable[dsti] = ds_eg;
}
}
//对两个节点添加边，以及权重关系 src代表起点 dst代表中点 w代表权重
void AddEdge(const V& src, const V& dst, const W& w)
{
size_t srci = GetVertexIndex(src);
size_t dsti = GetVertexIndex(dst);
_AddEdge(srci, dsti, w);
}
void Print()
{
//顶点和下标的映射关系
for (size_t i = 0; i < _vertexs.size(); ++i)
cout << "[" << i << "]" << "->" << _vertexs[i] << endl; //下标映射顶点集合
cout << endl;
//打印出边表
cout << "打印出边表:" << endl;
for (size_t i = 0; i < _linktable.size(); ++i)
{
cout << _vertexs[i] << "[" << i << "]->";
Edge* cur = _linktable[i];
while (cur)
{
cout << _vertexs[cur->_dsti] << "[" << cur->_dsti << "]:" << cur->_w << "->";
cur = cur->_next;
}
cout << "nullptr" << endl;
}
cout << endl;
//打印入边表
}
private:
map<V, size_t> _IndexMap; //建立顶点和下标之间的关系，方便我们根据顶点去找他的下标 比如两个顶点是否存在关系，就可以快速找到两个顶点的下标，然后去邻接矩阵看一下
vector<V> _vertexs; // 顶点集合
vector<Edge*> _linktable;
};
}2.5 邻接矩阵和邻接表的优劣性
最关键的问题就是：1，两个顶点是否相连。2，相连的权值是多少。
邻接矩阵：
1，邻接矩阵的存储方式非常适合稠密图
2，邻接矩阵O（1）判断两个顶点的连接关系，并取到权值
3,不适合查找一个顶点连接的所有边——O(N)
邻接表：
1，邻接表的存储方式非常适合稀疏图
2，适合找一个顶点连出去的所有边
3，不适合确定两点是否相连以及权值——O(N)
三、图的遍历方式
3.1 广度优先遍历
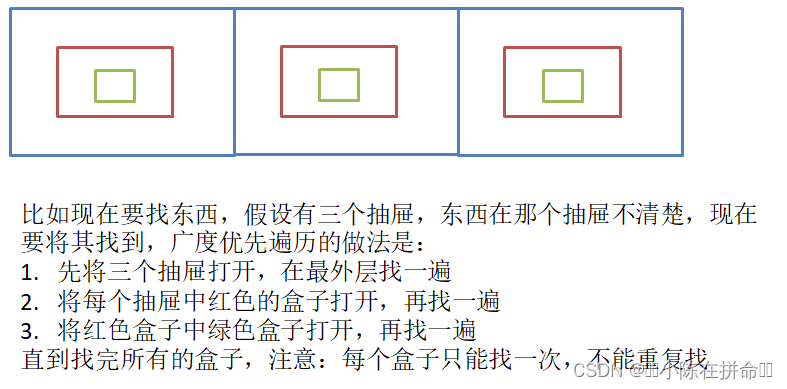
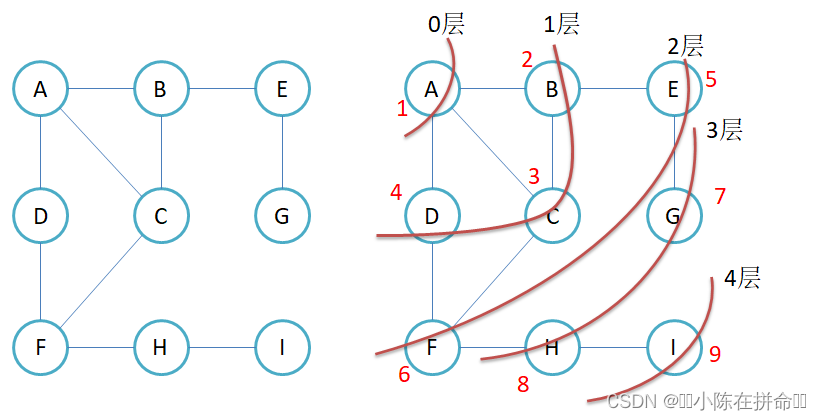
每访问一个结点，我们就将与他相连的顶点入队列，但是我们在入队列的时候需要用一个标记数组标记一下，这样可以避免 比如说A出的时候，BCD进，而B出的时候ACE进，如果用了标记数组，那么重复的AC就不会再入队列了。
层序遍历 但是没有一层一层出
void BFS(const V& src) //src表示我们的起点
{
size_t srci = GetVertexIndex(src);//找到起点的下标
queue<int> q;//存储下标的队列
size_t n = _vertexs.size();//表示有多少个节点
vector<bool> check(n);
q.push(srci);
check[srci] = true;//入队列就标记
while (!q.empty())
{
int front = q.front();//取队头
q.pop();
cout << _vertexs[front] << ":"<<front<<endl;
//然后让他的朋友进
for (size_t i = 0; i < n; ++i)
if (_matrix[front][i] != MAX_W && check[i] == false)
{
q.push(i);
check[i] = true;
}
}
}我们来看看美团的一道经典OJ
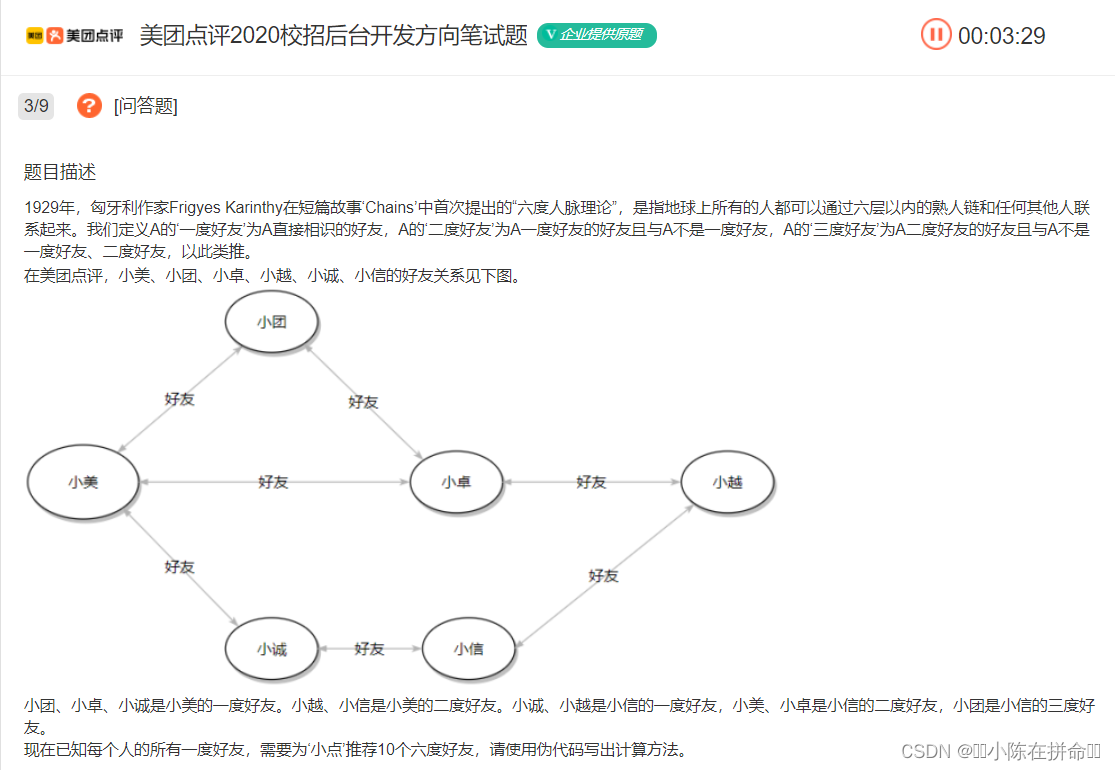也就是说我们得去找到他的六度好友，方法就是在层序遍历的时候，我们要控制一层一层出！
所以我们将BFS修改一下，控制成一行一行出（类似二叉树的层序遍历控制一行一行出）
//控制一层一层出 (常见的应用：找几度好友)
void BFS(const V& src) //src表示我们的起点
{
size_t srci = GetVertexIndex(src);//找到起点的下标
queue<size_t> q;//存储下标的队列
size_t n = _vertexs.size();//表示有多少个节点
vector<bool> check(n);
q.push(srci);
check[srci] = true;//入队列就标记
while (!q.empty())
{
//控制一层一层出
size_t sz = q.size();
for (size_t i = 0; i < sz; ++i) //一层出完了再去走下一层
{
size_t front = q.front();//取队头
q.pop();
cout << front << ":" << _vertexs[front] << " ";
//然后让他的朋友进
for (size_t i = 0; i < n; ++i)
if (_matrix[front][i] != MAX_W && check[i] == false)
{
q.push(i);
check[i] = true;
}
}
cout << endl;
}3.2 深度优先遍历
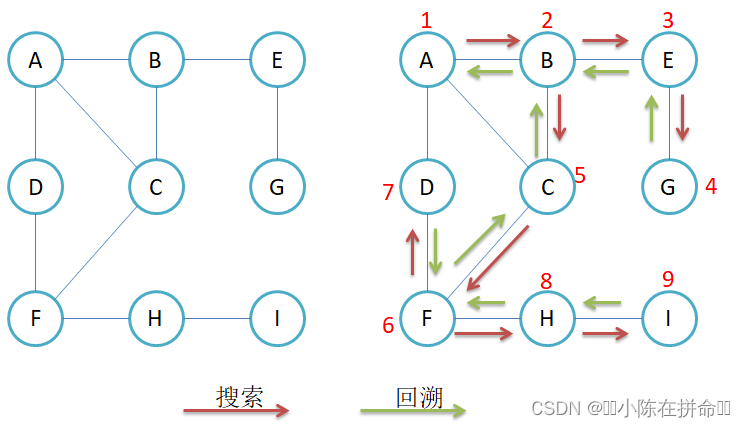
void _DFS(size_t srci, vector<bool>& check) //下一个位置的起点以及需要一个标记数组
{
cout << srci << ":" << _vertexs[srci] << " " << endl; //先访问 然后标记为访问过
check[srci] = true;
for (size_t i = 0; i < _vertexs.size(); ++i)
if (_matrix[srci][i] != MAX_W && check[i] == false)
_DFS(i, check);
}
void DFS(const V& src) //需要有一个起点
{
size_t srci = GetVertexIndex(src);//找到起点的下标
vector<bool> check(_vertexs.size()); //标记数组
_DFS(srci, check);
//如果是一个非连通图，可以在后面再进行一层检查check数组，然后对false的数组再进行一次访问
}如果我们遍历的图并不是连通图 那么最后可能会有一些结点访问不到，所以这个时候我们的解决方案就是遍历一次check数组，如果其中有false，那就以这个false为起点再走深度优先遍历，保证把剩下的结点遍历完。
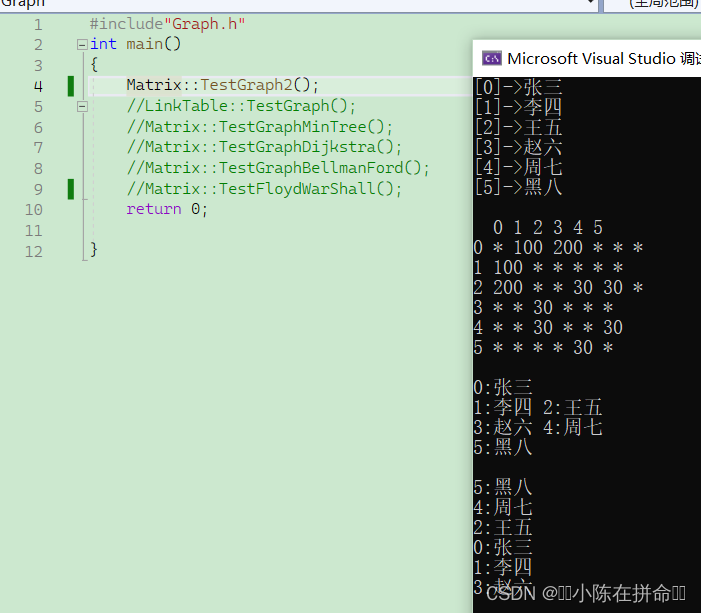
给大家附上一个测试用例：
void TestGraph2()
{
string a[] = { "张三", "李四", "王五", "赵六" ,"周七","黑八" };
int n = sizeof(a) / sizeof(a[0]);
Graph<string, int> g1(a, n);
g1.AddEdge("张三", "李四", 100);
g1.AddEdge("张三", "王五", 200);
g1.AddEdge("王五", "赵六", 30);
g1.AddEdge("王五", "周七", 30);
g1.AddEdge("黑八", "周七", 30);
g1.Print();
g1.BFS("张三");
cout << endl;
g1.DFS("黑八");
}
下一次博主会重点介绍图论的相关算法！！感谢支持！！
