暴力查找

暴力搜索是最简单的最近邻搜索，通过遍历整个点集，计算它们和目标点之间的距离，同时记录下来当前的最邻近点。这是一种较为初级朴素的算法，可应用于较小规模的点集。但是对于点集的数量级和空间维数交较大的情况则不适用。对于D维的N个样本点集，暴力查找的复杂度为O(DN)

ANNOY(Approximate Nearest Neighbors Oh Yeah)

算法原理

为简化并能说明问题，以2D数据来介绍下ANNOY算法原理，下图即为一个2D的数据分布图，

1 建立索引过程

Annoy 的目标是建立一个数据结构，使得查询一个点的最近邻点的时间复杂度是次线性。Annoy 通过建立一个二叉树来使得每个点查找时间复杂度是 O(log n)。 看下面这个图， 随机选择两个点，以这两个节点为初始中心节点，执行聚类数为 2 的 kmeans 过程，最终产生收敛后两个聚类中心点。这两个聚类中心点之间连一条线段（灰色短线），建立一条垂直于这条灰线，并且通过灰线中心点的线（黑色粗线）。这条黑色粗线把数据空间分成两部分。在多维空间的话，这条黑色粗线可以看成等距垂直超平面。

在两个子空间内，重复上述步骤继续划分，如下图：

在划分的子空间内进行不停的递归迭代继续划分，直到每个子空间最多只剩下K个数据节点，如下图：

通过多次递归迭代划分的话，最终原始数据会形成类似下面这样一个二叉树结构。二叉树底层是叶子节点记录原始数据节点，其他中间节点记录的是分割超平面的信息。Annoy建立这样的二叉树结构是希望满足这样的一个假设:相似的数据节点应该在二叉树上位置更接近，一个分割超平面不应该把相似的数据节点分割二叉树的不同分支上。

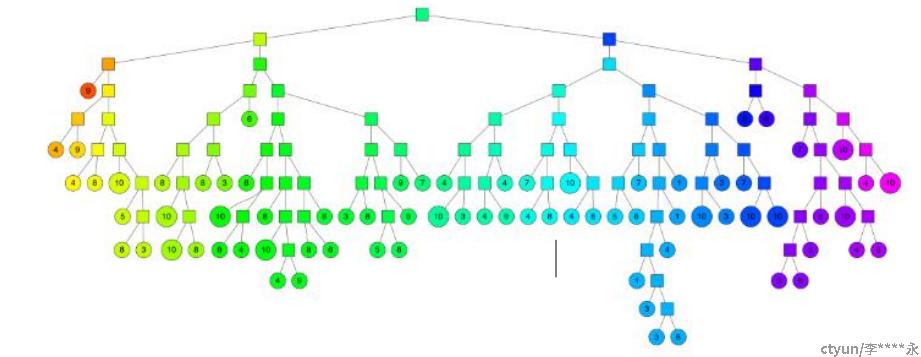
2 搜索查询过程

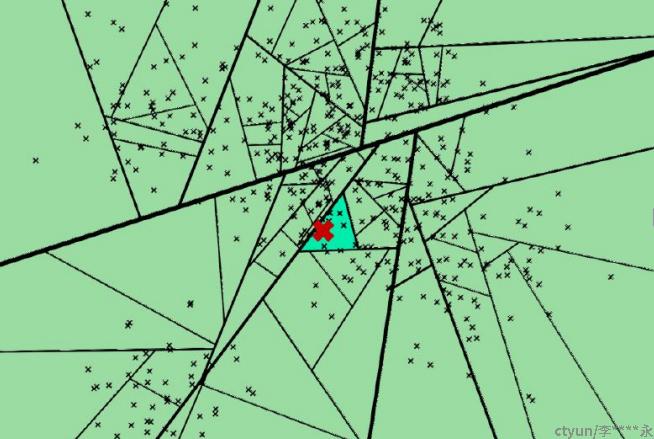
索引构建完成后，怎么用来查询呢？例如在上图中的红色节点。查找的过程就是不断看他在分割超平面的哪一边。从二叉树索引结构来看，如下图，就是从根节点不停的往叶子节点遍历的过程。通过对二叉树每个中间节点（分割超平面相关信息）和查询数据节点进行相关计算来确定二叉树遍历过程是往这个中间节点左孩子节点走还是右孩子节点走。通过以上方式完成查询过程。

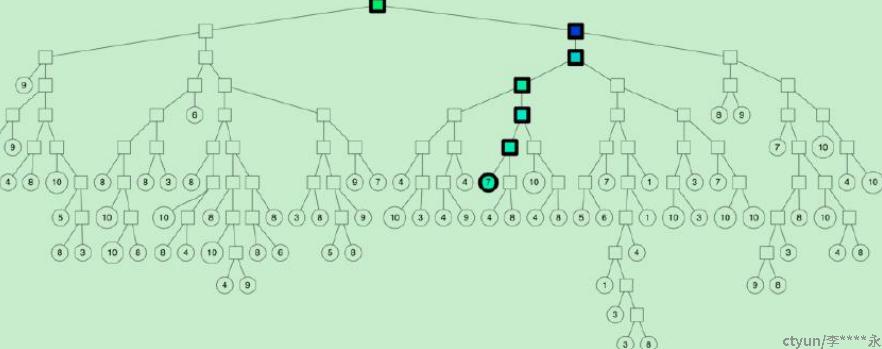
但是上述描述存在两个问题：

（1）查询过程最终落到叶子节点的数据节点数小于我们需要的TopN相似邻居节点数目怎么办？

（2）两个相近的数据节点划分到二叉树不同分支上怎么办？

针对这个问题可以通过两个方法来解决：

（1）采用优先队列机制：采用一个优先队列来遍历二叉树，从根节点往下的路径，根据查询节点与当前分割超平面距离（

margin）进行排序。如果分割超平面的两边都很相似，那可以两边都遍历；下面是是个示意图：

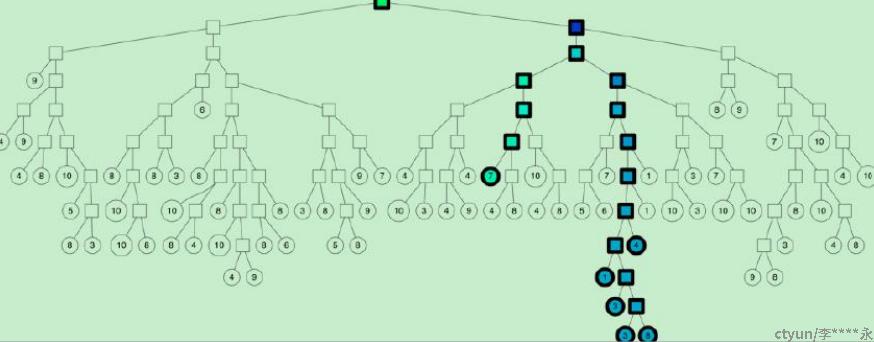
（2）建立多棵二叉树树，构成一个森林，每个树建立机制都如上面所述那样。多棵树示意图如下所示：

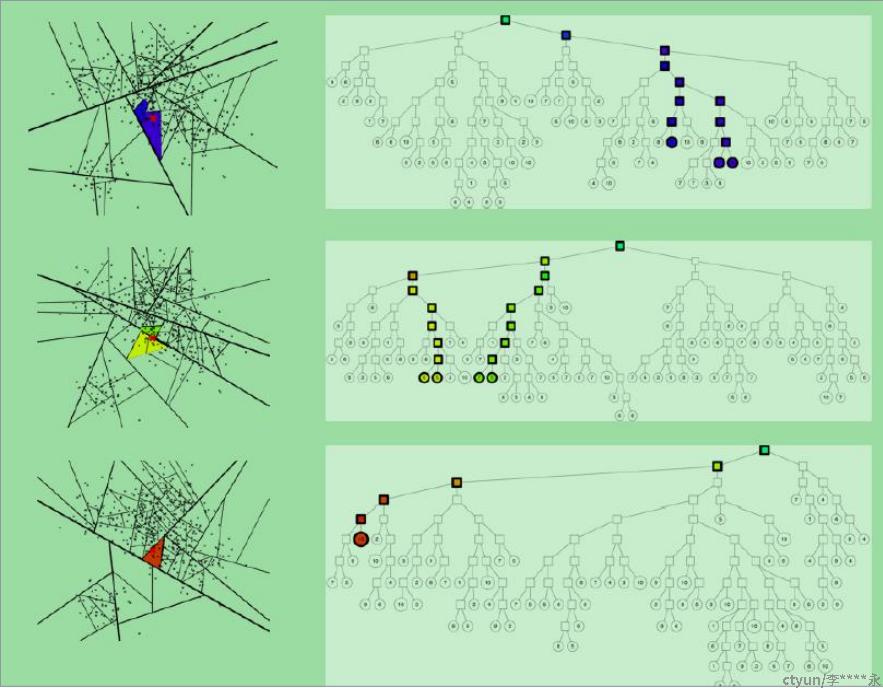
3 返回最终近邻节点

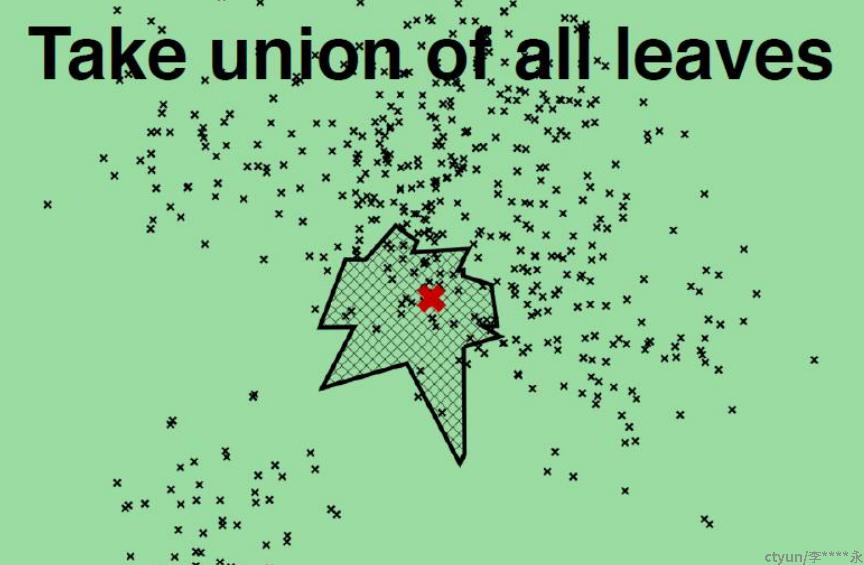
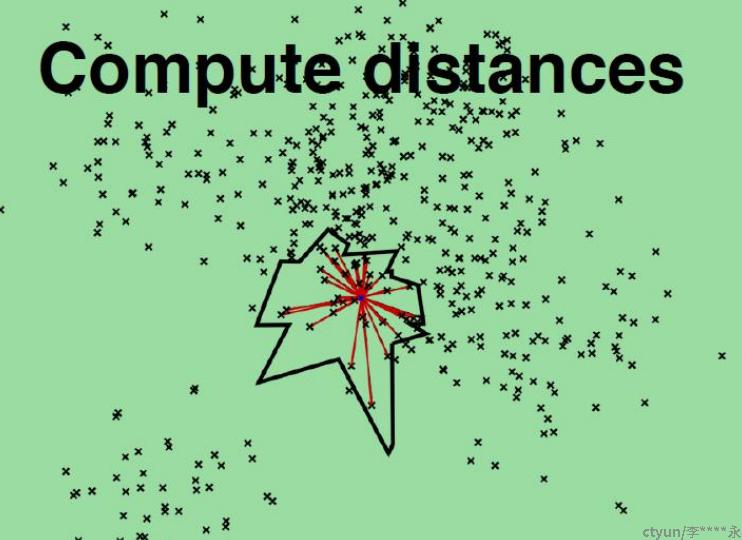
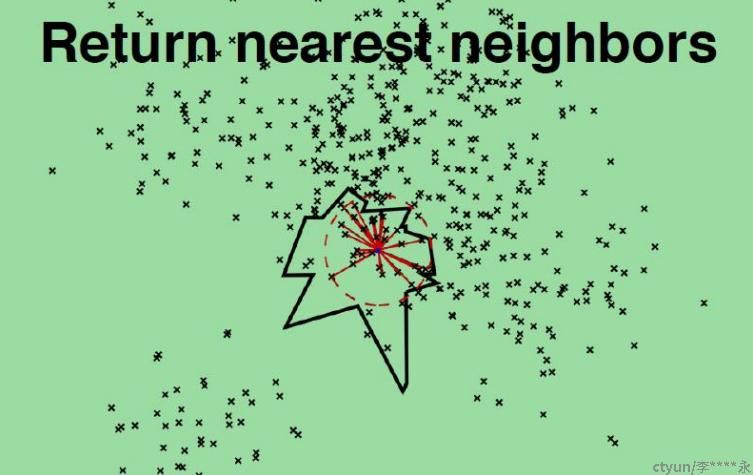
每棵树都返回一堆近邻点后，如何得到最终的TopN相似集合呢？首先所有树返回近邻点都插入到优先队列中，求并集去重,然后计算和查询点距

离，最终根据距离值从近距离到远距离排序，返回TopN近邻节点集合。

基于人脸搜索的算法实战

1. 距离计算，采用归一化的欧氏距离：distance=sqrt(2-2*cos(u,v))，等价于余弦距离。

2. 向量维度较小<100）,即使维度到达1000变现也不错

3. 索引创建与查找分离（特别是一旦树已经创建，就不能添加更多项）

4. 参数n_trees在构建时提供，并影响构建时间和索引大小。较大的值将给出更准确的结果，但更大的索引。search_k在运行时提供，并影响搜索性能。较大的值将给出更准确的结果，但将需要更长的时间返回。如果不提供search_k，它将默认为n*n_trees，其中n是近似最近邻的数目（topN)。否则，search_k和n_tree大致是独立的，即如果search_k保持不变，n_tree的值不会影响搜索时间，反之亦然。基本上，建议在可用负载量的情况下尽可能大地设置n_trees，并且考虑到查询的时间限制，建议将search_k设置为尽可能大。

5. 代码时间简洁清晰，方便定制化修改二次开发。

参考资料：

官网地址：https://github.com/spotify/annoy