当前已有的大部分图神经网络算法包括用于同构图的GCN、GraphSage、GAT等或者用于异构图的HAN等算法都是在建好图的基础上进行图表征的学习，也就是说建图和图表征是分离的。而 Deep Iterative and Adaptive Learning for Graph Neural Networks (DIAL-GNN)提出了一种图的构建和图的表征端到端进行学习的方法。

相比于Learning Discrete Structures for Graph Neural Networks（LDS-GNN）仅仅支持直推式学习（Transductive learning），DIAL-GNN既可以支持直推式学习（Transductive learning）也可以支持归纳式学习（Inductive learning）。

给定一个包含n个节点对象的集合V个一个特征矩阵X ∈ Rd×n，目标是自动的学习一个图结构G，通常是一种邻接矩阵A ∈ Rn×n 的形式。

 

1.1 相似度量学习

作者设计了一种多头的加权余弦相似度：

 

其中 ⊙ 表示哈达玛积，使用m个和输入向量相同维度的权重向量独立地计算m个余弦相似度，每一个权重向量代表一种语义，其实就是每一对节点从m个不同的语义或角度去分别去计算一个余弦相似度，然后取m个余弦相似度的均值作为这一对节点最终的相似度。最终得到一个相似度矩阵S， Sijk 是两个输入节点向量 vi 和 vj 在第k个语义上的相似性，其中权重参数w是通过学习得到的，这个思想类似于大家常用的多头注意力机制。

 

1.2 稀疏矩阵提取

一方面邻接矩阵通常是非负的，然而 Sij 的取值范围确实[-1, 1], 另一方面大部分图网络其实相对于全连接图来说是比较稀疏的，全连接图中有一些连接是无用的或无意义的，而且会增大计算量，因此作者通过设置一个非负阈值 （我该怎么来编辑这个字符呢，哎，这编辑器，yibuqige， 这样吧就）来从学习到的相似矩阵S中提取一个邻接矩阵A：

 

2 图正则化

在图信号处理中，一个被广泛采用的假设是图中相邻节点之间的变化是比较平滑的，给定一个无向图和对应的加权对称邻接矩阵A，一个包含n个图信号的集合 x1,...,x2 ∈ Rn 的平滑度通常通过狄利克雷能量（Dirichlet energy）来度量：

 

tr(.)是矩阵的迹，L = D - A 是图的拉普拉斯矩阵，D是各个节点度的矩阵，是一个对角矩阵。从上面的式子可以看出要最小化 Ω (A, X)是在强制相邻的节点有相同的特征，因此强制基于邻接矩阵A相关联的图信号趋于平滑。然而仅仅是最小化上面的平滑度损失，最终会得到一个无效解A = 0。而且通常是希望能够控制图的稀疏程度。因此根据 (Kalofolias 2016）对图的学习增加了额外的限制：

 

 

 

其中 ||.||F 是矩阵的范数。上式的第一项通过log屏障（根据log函数的性质，如果变量值太小，那么函数值会趋于无穷）对非联通图进行惩罚，即趋向于使图去建立连接，第二项控制了图的稀疏性，因为如果||A||越小图越稀疏，该惩罚即趋向于使图稀疏。

借助于上面的技术对通过等式（1）、（2）学到的图进行正则化，整个图正则化随时是上面两个损失的和，即控制了平滑性又控制了连通性和稀疏性：

 

其中 都是非负的超参数。

 

3 基于迭代的图学习方法

 

3.1 图结构和图表示学习相结合

 

一组节点的图结构需要满足两个目标：i）通过度量机制或度量函数（Eq. (1)）和平滑损失（Eq. (3)）的限制能够代表节点之间的语义信息；ii)能够满足下游的预测任务。不同于之前基于图正则化损失或具体任务的预测损失去直接优化邻接矩阵，DIAL是通过最小化图正则化损失和具体任务的预测损失的联合损失函数去学习，L = Lpred + Lg

可以发现这个图学习框架对各种GNN算法和预测任务的变量是不感知的，在这篇论文中，作者采用了一个两层的GCN，第一层将节点的特征映射到节点的嵌入空间(Eq. (6))，第二层将节点嵌入映射到输出空间 (Eq. (7)) 。

 

其中 A 是归一化的矩阵， 是具体任务的输出函数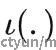， 是具体任务的损失函数

那么临界举着 A是怎么得到的呢？通过之前的实验显示完全抛弃图原来的拓扑结构，完全通过端到端的去学习效果并不好，因此在优化图结构就是在原有图结构的基础上做小的变换的假设下，论文中作者将学习到的图结构和图原来的图结构做结合得到最终的邻接矩阵 A ，

 

其中 L0 是图初始的归一化的邻接矩阵， L0=D0−1/2A0D0−1/2 ， D0 是节点的度的矩阵。通过Eqs. (1) and (2)学习到的邻接矩阵行归一化的，因此每一行的和为1。  是一个超参数用于平衡学习到的图结构和原始的图结构。如果原始的图结构不存在，那么可以基于余弦相似度通过KNN来构建图结构。

 

3.2 用于图学习的迭代方法

先前的一些研究仅仅基于一些注意力机制使用原始的节点特征去学习图结构，通过作者的实验这样并不能学习到很好的图结构，即使是通过和预测损失联合进行端到端的学习。因为相似度的度量是基于可能并不充分的原始节点特征来计算的。

为了解决这个限制，作者提出了深度迭代和适应学的学习框架（DIAL-GNN），算法如Algorithm 1。除了根据原始的特征计算节点的相似性，还引入了可学习的基于中间节点嵌入计算的度量机制或度量函数(Eq. (1))，如第10行所示，在该节点嵌入空间上定义的度量函数学习到的拓扑信息是仅基于原始节点特征学习到的拓扑信息的补充。

 

 

结合原始节点特征和节点嵌入的优点，将最终学习的图形结构做线性组合：

 

 

 

其中 A（t） 和 A（0）分别是通过Eq. (9)在第t次迭代和迭代之前的初始化步骤中学习到的归一化邻接矩阵。同时从第10行和第12行可以看到算法每次迭代都会用更新后的节点嵌入 Z（t-1）来改进邻接矩阵 A（t），然后用更新后的邻接矩阵 A（t）来改进节点嵌入 Z（t） ,当邻接矩阵收敛到阈值  或者达到最大的迭代次数的时候停止迭代。在每一次迭代中，任务的预测损失和图正则化损失通过BP（反向传播）到上一次的迭代去更新模型参数。

 

3.3 模型收敛性

当我们在自己设计loss的时候，只有loss是可收敛的，那么训练的时候模型才能收敛，学习到最有货局部最优的解，但正如论文中说的，由于所涉及的学习模型的复杂性，从理论上证明所提出的迭代学习过程的收敛性是一个挑战，所以作者没有通过理论推导去证明loss具有收敛性，而是从概念上去说明了它能够工作的原因，而且从作者的实验也可以看出模型可以很快的收敛。

下图展示了经过学习的邻接矩阵A和中间过程中节点的嵌入矩阵Z在迭代过程中的信息流：

 

 

 

 

 

4 为什么DIAL-GNN即支持直推式学习（Transductive learning）也可以支持归纳式学习（Inductive learning）而LDS-GNN却只支持直推式学习（Transductive learning）

因为DIAL学习图结构本质上还是机遇节点的相似性的，只不过在相似性度量上进行了扩展，加入了可学习的语义参数W，因此只要学习到了W，那么即使是推理预测是有不同与训练集的新的节点，那么也可通过W计算出新节点与其他节点的相似性的。而LDS学习图的结构本质上是在解决双层规划问题（Bilevel Programming），学习到的是节点与节点之间的一种伯努利分布，如果在推理预测是有新的节点加入，那么新的节点是不知道与其他节点的连接概率的，也没有通过学习到的参数来计算这个概率，因此需要重新训练。