二分查找的难点在于到底要给 mid 加⼀还是减⼀，while ⾥到底⽤ <= 还是 < 。
另外声明⼀下，计算 mid 时需要防⽌溢出，代码中 left + (right - left) / 2 就和 (left + right) / 2 的结果相同，但是有效防⽌了 left 和 right 太⼤直接相加导致溢出。
⼀、寻找⼀个数（基本的⼆分搜索）
示例代码1：
int binarySearch(int[] nums, int target) {
int left = 0;
int right = nums.length - 1; // 注意
while(left <= right) {
int mid = left + (right - left) / 2;
if(nums[mid] == target)
return mid;
else if (nums[mid] < target)
left = mid + 1; // 注意
else if (nums[mid] > target)
right = mid - 1; // 注意
}
return -1;
}示例代码2：【python】
def binary_search(lst, target):
left = 0
right = len(lst) - 1
while left <= right:
mid = int(left + (right - left) / 2)
if lst[mid] == target:
return mid
elif lst[mid] < target:
left = mid + 1
else:
right = mid - 1
return -1
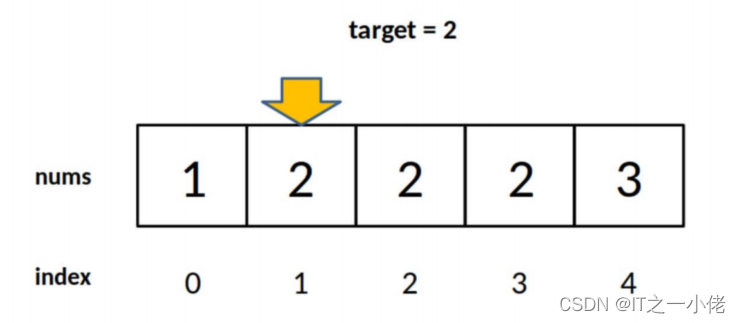
lst = [1, 2, 2, 2, 3]
target = 2
ret = binary_search(lst, target)
print(ret)
1、为什么 while 循环的条件中是 <=，⽽不是 <？
初始化 right 的赋值是 nums.length - 1 ，即最后⼀个元素的索引，⽽不是 nums.length 。
这⼆者可能出现在不同功能的⼆分查找中，区别是：前者相当于两端都闭区间 [left, right] ，后者相当于左闭右开区间 [left, right) ，因为索引⼤⼩为 nums.length 是越界的。
上述算法中使⽤的是前者 [left, right] 两端都闭的区间。 这个区间 其实就是每次进⾏搜索的区间 。
while(left <= right) 的终⽌条件是 left == right + 1 ，写成区间的形式就是 [right + 1, right] ，或者带个具体的数字进去 [3, 2] ，可⻅ 这时候 区间为空 ，因为没有数字既⼤于等于 3 ⼜⼩于等于 2 的吧。所以这时候while 循环终⽌是正确的，直接返回 -1 即可。
while(left < right) 的终⽌条件是 left == right ，写成区间的形式就是[left, right] ，或者带个具体的数字进去 [2, 2] ， 这时候区间⾮空 ，还有⼀个数 2 ，但此时 while 循环终⽌了。也就是说这区间 [2, 2] 被漏掉了，索引 2 没有被搜索，如果这时候直接返回 -1 就是错误的。
2 、为什么 left = mid + 1 ， right = mid - 1 ？我看有的代码是 right = mid 或者 left = mid ，没有这些加加减减，到底怎么回事，怎么判断 ？
这是⼆分查找的⼀个难点。 上个问题明确了「搜索区间」这个概念，⽽且本算法的搜索区间是两端都闭的，即 [left, right] 。那么当发现索引 mid 不是要找的 target 时，下⼀步应该去搜索哪⾥呢？当然是去搜索 [left, mid-1] 或者 [mid+1, right] 对不对？ 因为 mid 已 经搜索过，应该从搜索区间中去除 。
3 、二分搜索算法存在的缺陷 ？
⽐如有序数组 nums = [1,2,2,2,3] ， target 为 2 ，此算法返回的索引是 2 ，没错。但是如果想得到 target 的左侧边界，即索引 1 ，或者想得到 target 的右侧边界，即索引 3 ，这样的话此算法是⽆法处理的。
这样的需求很常⻅，你也许会说，找到⼀个 target ，然后向左或向右线性搜 索不⾏吗？可以，但是不好，因为这样难以保证⼆分查找对数级的复杂度 了 。
⼆、寻找左侧边界的⼆分搜索
示例代码1：
int left_bound(int[] nums, int target) {
if (nums.length == 0) return -1;
int left = 0;
int right = nums.length; // 注意
while (left < right) { // 注意
int mid = (left + right) / 2;
if (nums[mid] == target) {
right = mid;
} else if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid; // 注意
}
}return left;
}示例代码2： 【python】【此时代码中存在小问题，详见后面代码】
def binary_search(lst, target):
if len(lst) == 0:
return -1
left = 0
right = len(lst)
while left < right:
mid = int(left + (right - left) / 2)
if lst[mid] == target:
right = mid
elif lst[mid] < target:
left = mid + 1
else:
right = mid
return left
lst = [1, 2, 2, 2, 3]
target = 2
ret = binary_search(lst, target)
print(ret)
1 、为什么 while 中是 < ⽽不是 <= ?
因为 right = nums.length ⽽不是 nums.length - 1 。因此每次循环的「搜索区间」是 [left, right) 左闭右开。
while(left < right) 终⽌的条件是 left == right ，此时搜索区间 [left,left) 为空，所以可以正确终⽌。
2 、为什么没有返回 -1 的操作？如果 nums 中不存在 target 这个值，怎 么办 ？
答：因为要⼀步⼀步来，先理解⼀下这个「左侧边界」有什么特殊含义：
对于这个数组，算法会返回 1 。这个 1 的含义可以这样解读： nums 中⼩于 2 的元素有 1 个。
⽐如对于有序数组 nums = [2,3,5,7] , target = 1 ，算法会返回 0 ，含义是： nums 中⼩于 1 的元素有 0 个。
再⽐如说 nums = [2,3,5,7], target = 8 ，算法会返回 4 ，含义是： nums中⼩于 8 的元素有 4 个。
综上可以看出，函数的返回值（即 left 变量的值）取值区间是闭区间[0, nums.length] ，所以简单添加两⾏代码就能在正确的时候 return -1：
while (left < right) {
//...
}// target ⽐所有数都⼤
if (left == nums.length) return -1;
// 类似之前算法的处理⽅式
return nums[left] == target ? left : -1;将上述示例2python代码整体修改后为：
def binary_search(lst, target):
if len(lst) == 0:
return -1
left = 0
right = len(lst)
while left < right:
mid = int(left + (right - left) / 2)
if lst[mid] == target:
right = mid
elif lst[mid] < target:
left = mid + 1
else:
right = mid
# target比所有数都大
if left == len(lst):
return -1
# 类似之前的代码处理
return left if lst[left] == target else -1
lst = [1, 2, 2, 2, 3]
target = 5
ret = binary_search(lst, target)
print(ret)
3 、为什么 left = mid + 1 ， right = mid ？和之前的算法不⼀样 ？
答：这个很好解释，因为我们的「搜索区间」是 [left, right) 左闭右开，所以当 nums[mid] 被检测之后，下⼀步的搜索区间应该去掉 mid 分割成两个区间，即 [left, mid) 或 [mid + 1, right) 。
4 、为什么该算法能够搜索左侧边界 ？
答：关键在于对于 nums[mid] == target 这种情况的处理：
if (nums[mid] == target)
right = mid; 可⻅，找到 target 时不要⽴即返回，⽽是缩⼩「搜索区间」的上界right ，在区间 [left, mid) 中继续搜索，即不断向左收缩，达到锁定左侧边界的⽬的。
5 、为什么返回 left ⽽不是 right ？
答：都是⼀样的，因为 while 终⽌的条件是 left == right 。
示例代码：
def binary_search(lst, target):
if len(lst) == 0:
return -1
left = 0
right = len(lst)
while left < right:
mid = int(left + (right - left) / 2)
if lst[mid] == target:
right = mid
elif lst[mid] < target:
left = mid + 1
else:
right = mid
# target比所有数都大
if right == len(lst):
return -1
# 类似之前的代码处理
return right if lst[right] == target else -1
lst = [1, 2, 2, 2, 3]
target = 2
ret = binary_search(lst, target)
print(ret)
6 、能不能想办法把 right 变成 nums.length - 1 ，也就是继续使⽤两边都 闭的「搜索区间」？这样就可以和第⼀种⼆分搜索在某种程度上统⼀起来 了 。
答：当然可以，只要明⽩了「搜索区间」这个概念，就能有效避免漏掉元素，随便你怎么改都⾏。下⾯我们严格根据逻辑来修改：
因为你⾮要让搜索区间两端都闭，所以 right 应该初始化为 nums.length - 1 ， while 的终⽌条件应该是 left == right + 1 ，也就是其中应该⽤ <= ：
int left_bound(int[] nums, int target) {
// 搜索区间为 [left, right]
int left = 0, right = nums.length - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
// if else ...
}因为搜索区间是两端都闭的，且现在是搜索左侧边界，所以 left 和 right 的更新逻辑如下：
if (nums[mid] < target) {
// 搜索区间变为 [mid+1, right]
left = mid + 1;
} else if (nums[mid] > target) {
// 搜索区间变为 [left, mid-1]
right = mid - 1;
} else if (nums[mid] == target) {
// 收缩右侧边界
right = mid - 1;
} 由于 while 的退出条件是 left == right + 1 ，所以当 target ⽐ nums 中所有元素都⼤时，会存在以下情况使得索引越界：
因此，最后返回结果的代码应该检查越界情况：
if (left >= nums.length || nums[left] != target)
return -1;
return left;完整代码如下：
def binary_search(lst, target):
if len(lst) == 0:
return -1
left = 0
right = len(lst) - 1
while left <= right:
mid = int(left + (right - left) / 2)
if lst[mid] == target:
# 收缩右边界
right = mid - 1
elif lst[mid] < target:
# 搜索区间变为[mid + 1, right]
left = mid + 1
else:
# 搜索区间变为[left, mid - 1]
right = mid - 1
# 检查出界情况
if left >= len(lst) or lst[left] != target:
return -1
return left
lst = [1, 2, 2, 2, 3]
target = 2
ret = binary_search(lst, target)
print(ret)
三、寻找右侧边界的⼆分查找
类似寻找左侧边界的算法，这⾥也会提供两种写法，还是先写常⻅的左闭右开的写法，只有两处和搜索左侧边界不同，已标注：
示例代码1： 【注意：此时下面代码存在一些未考虑的细节，详见下面】
int right_bound(int[] nums, int target) {
if (nums.length == 0) return -1;
int left = 0, right = nums.length;
while (left < right) {
int mid = (left + right) / 2;
if (nums[mid] == target) {
left = mid + 1; // 注意
} else if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid;
}
}
return left - 1; // 注意
}示例代码2： 【python】【此时代码存在一些问题，详见后面代码】
def right_bound(lst, target):
if len(lst) == 0:
return -1
left = 0
right = len(lst)
while left < right:
mid = int(left + (right - left) / 2)
if lst[mid] == target:
left = mid + 1
elif lst[mid] < target:
left = mid + 1
else:
right = mid
return left - 1
lst = [1, 2, 2, 2, 3]
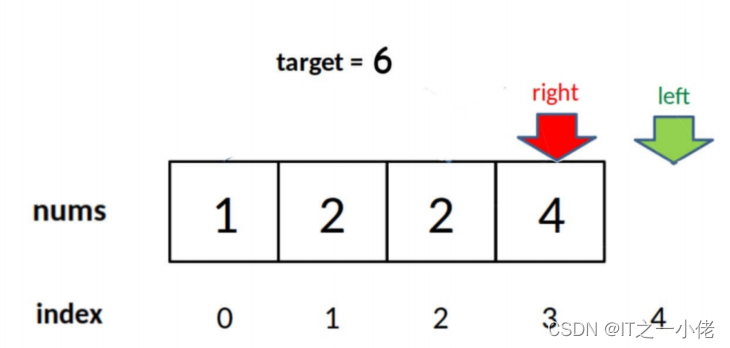
target = 2
ret = right_bound(lst, target)
print(ret)
1 、为什么这个算法能够找到右侧边界 ？
答：类似地，关键点还是这⾥：
if (nums[mid] == target) {
left = mid + 1; 当 nums[mid] == target 时，不要⽴即返回，⽽是增⼤「搜索区间」的下界 left ，使得区间不断向右收缩，达到锁定右侧边界的⽬的。
2 、为什么最后返回 left - 1 ⽽不像左侧边界的函数，返回 left ？⽽且 我觉得这⾥既然是搜索右侧边界，应该返回 right 才对 。
答：⾸先， while 循环的终⽌条件是 left == right ，所以 left 和 right是⼀样的，你⾮要体现右侧的特点，返回 right - 1 好了。
⾄于为什么要减⼀，这是搜索右侧边界的⼀个特殊点，关键在这个条件判断：
if (nums[mid] == target) {
left = mid + 1;
// 这样想: mid = left - 1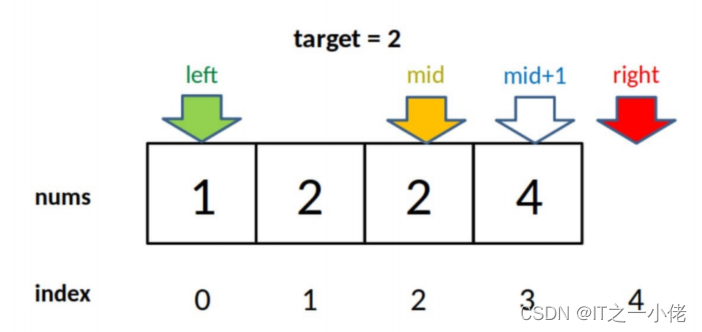
因为我们对 left 的更新必须是 left = mid + 1 ，就是说 while 循环结束时， nums[left] ⼀定不等于 target 了，⽽ nums[left-1] 可能是 target 。
3 、为什么没有返回 -1 的操作？如果 nums 中不存在 target 这个值，怎 么办 ？
答：类似之前的左侧边界搜索，因为 while 的终⽌条件是 left == right ，就是说 left 的取值范围是 [0, nums.length] ，所以可以添加两⾏代码， 正确地返回 -1 ：
while (left < right) {
// ...
}
if (left == 0) return -1;
return nums[left-1] == target ? (left-1) : -1;完整代码如下：
def right_bound(lst, target):
if len(lst) == 0:
return -1
left = 0
right = len(lst)
while left < right:
mid = int(left + (right - left) / 2)
if lst[mid] == target:
left = mid + 1
elif lst[mid] < target:
left = mid + 1
else:
right = mid
if left == 0:
return -1
return left - 1 if lst[left-1] == target else -1
lst = [1, 2, 2, 2, 3]
target = 5
ret = right_bound(lst, target)
print(ret)
4、是否也可以把这个算法的「搜索区间」也统⼀成两端都闭的形式呢？
示例代码： 【python】
def right_bound(lst, target):
if len(lst) == 0:
return -1
left = 0
right = len(lst) - 1
while left <= right:
mid = int(left + (right - left) / 2)
if lst[mid] == target:
# 这⾥改成收缩左侧边界即可
left = mid + 1
elif lst[mid] < target:
left = mid + 1
else:
right = mid - 1
# 这⾥改为检查right越界的情况，⻅下图
if left < 0 or lst[right] != target:
return -1
return right
lst = [1, 2, 2, 2, 3]
target = 2
ret = right_bound(lst, target)
print(ret)
当 target ⽐所有元素都⼩时， right 会被减到 -1 ，所以需要在最后防⽌越界：
