📚️1.朴素二分

🚀1.1二分查找

1.1.1题目解析

给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target  ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。

当然题目很好理解，就是寻找一个目标值，然后返回目标值的下标，若没有就返回-1；那么如下例题所示：

1. 输入: nums= [-1,0,3,5,9,12], target= 9

输出: 4 解释: 9 出现在 nums中并且下标为 4

2. 输入：nums = [-1,0,3,5,6]，target = 4

输出：-1

 接下来就是小编对于这道题的理解

1.1.2算法分析

第一种：利用暴力算法

思路：不断循环遍历枚举，然后进行比较，若找到了就返回数组的下标；若目标值小于此时遍历的数组的某个元素，那么由于数组的升序排序的缘故，直接返回-1即可

 这里小编就不在进行代码编写了，比较简单

第二种：二分查找

什么是二分查找：

其实所谓的二分查找就是找出一个数组的二段性，然后根据这个二段性将数组分为两个部分，然后其中一部分可以进行舍去；（所以不管数组是否是升序还是乱序，找到二段性就可以使用二分算法） 

思路分析：

 具体思路就是在数组的左边和右边端点设置两个指针，指针之间就是一个区间，然后算出两个指针的中点，和左右指针分为两个部分，其中一部分小于或者大于就要更新区间范围；

如下图所示：

 

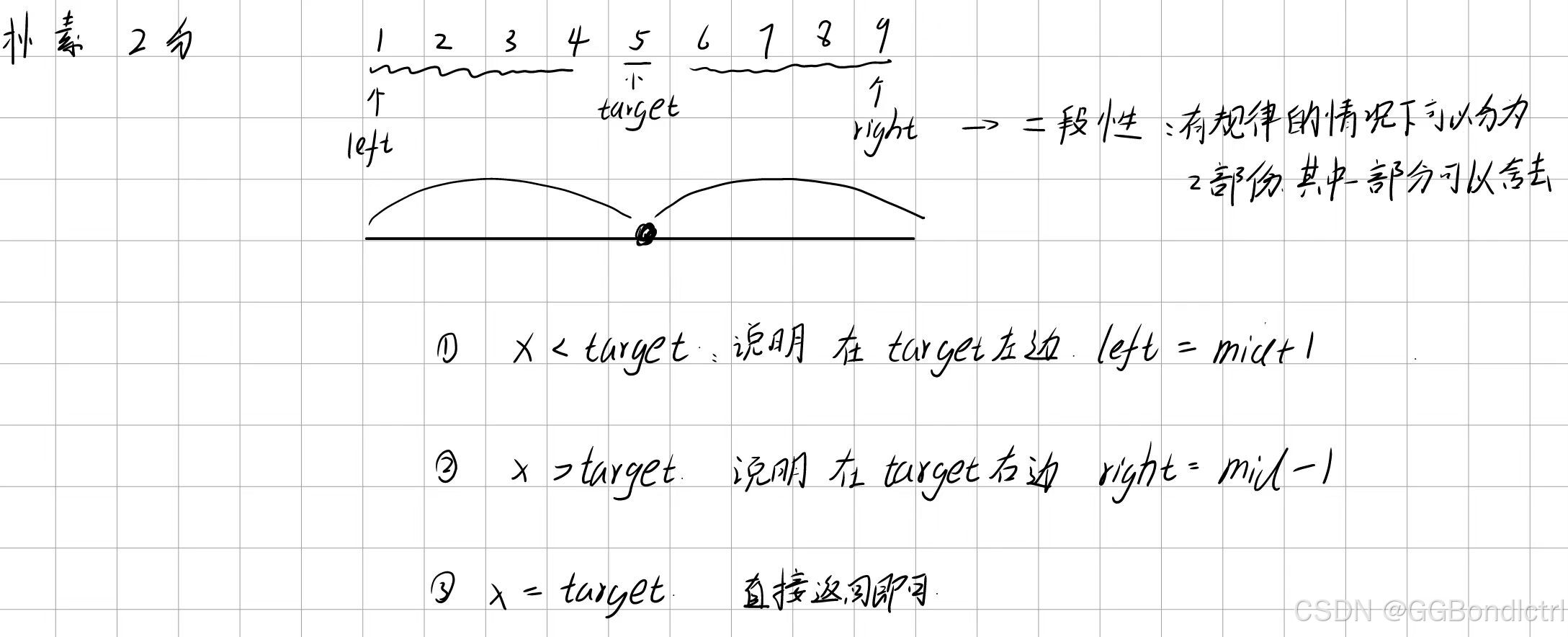
小编字写得不是很好，请见谅~~~

我们算出中点后，判断中点的值 nums[mid] 是否小于或者大于目标值target；

若小于target： 说明mid落在【left-target】之间，那么缩小范围就是left = mid + 1；

若大于target： 说明mid落在【target - right】之间，那么缩小范围就是right = mid - 1；

若等于目标值那么就可以直接返回即可；

我们举一个例子如下所示：

那么此时，一下就可以干掉一大部分的没有遍历意义的数据，直接快了许多；

1.1.3代码编写

具体的代码如下所示：

class Solution {
    public int search(int[] nums, int target) {
        // 二分查找算法
        int left = 0;
        int right = nums.length - 1;
        int mid = left + (right - left)/2;

        while (right >= left) {
            
            if(nums[mid] < target){
                left = mid + 1;
            }
            if(nums[mid] > target){
                right = mid -1;
            }
            if(nums[mid] == target){
                return mid;
            }
            mid = (left + right)/2;
        }
        return -1;
    }
}

这里的求中点的算法，为啥不直接left + right /2呢？小编这种是为了防止溢出的风险，所以小编使用减法实现的，就不会溢出了，这里使用的循环条件判断，假如所有的值都小于target，那么left会一直加，直到等于right，此时再次判断，那么不等于target，那么就直接返回-1即可了；

提示：一般优点难度的二分查找都不会使用这里的朴素二分，所以这道题模版就不进行编写了；

1.1.4时间复杂度

由于二分算法使用是每次干掉一半的数值；

• 第 1 次查找：在长度为  的区间内查找，比较中间元素后，剩余待查找区间长度变为n/2 。
• 第 2 次查找：基于上一次缩小后的区间，再比较中间元素，此时剩余待查找区间长度变为n/2*2 。
• 第 3 次查找：同理，剩余待查找区间长度变为n/2*2*2 。
• 以此类推：经过 k次查找后，剩余待查找区间长度变为n/2*2...... 。

所以经过变换后，两边同时以2为底的对数后，在算法复杂度分析中，通常忽略对数的底数（因为不同底数的对数之间仅相差一个常数因子）时间复杂度就是：logN

📚️2.非朴素二分

🚀2.1查找排列数组中元素第一个和最后一个位置

2.1.1题目解析

给你一个按照非递减顺序排列的整数数组 nums，和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。

如果数组中不存在目标值 target，返回 [-1, -1]。

你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。

其实大概意思就是：

在 5 5 7 7 8 8 8 9中查找8，那么开始位置为4，最后一个位置为6，那么输出就是[4 , 6]

2.1.2算法分析

 小编这里不进行暴力算法的分析了，直接步入正题

1.查找区间的左端点

其实这里的元素可以分为两部分：

 

如上图：第一部分是全部小于target的，那么另一部分就是全都大于或者等于target的；

所以根据二段性，此时就可调整区间了

 num[mid]  < target，在区间一号位，那么left = mid + 1，此时不肯能等于mid，因为mid指定的数本来就小于target，那么left 更新为mid + 1就可以了；

num[mid] >= target，那么在区间二号位，所以right = mid就可以了，为啥不是mid - 1，因为right刚好等于区间左端点的话，mid - 1就会超出正确区间；

细节问题：

 1.这里使用left < right ，还是 left < = right 呢？

答案是left  <  right ：

假如我们是left  <=  right，咱们看看一下例子：

 2   2    3      3    4      4, target = 1

那么此时就会满足大于 target ,此时right 就会一直加加，直到等于left ，那么此时一直等于left，mid又大于target，right = mid, 但是mid = right = left ，此时就会进入死循环 

2.取中点的时候使用left + (right - left)/2;还是left + (right - left + 1)/2;

此时我们还是举一个例子：

假如我们使用left + (right - left + 1)/2;

如下：

 

但是使用left + (right - left)/2;就不会出现这种情况；

2.查找区间右端点

如下图所示：

具体的步骤和上面区间左端点一致；

1.x <= target 的时候，在区间右端，那么left = mid，假如正好是花圈的位置，就不能+1，所以为left = mid;

 2.x > target的时候，子啊区间左端，right = mid - 1;

细节问题：

此时right  > left，这个是一致的，相遇了判断即可，无需进行循环；

但是在 left + (right - left)/2里会有一个缺陷：

 那么就直接使用 left + (right - left + 1)/2；

2.1.3代码编写

代码如下所示：

class Solution {
    public int[] searchRange(int[] nums, int target) {
        int[] ret = new int[2];
        ret[0] = ret[1] = -1;
        if (nums.length == 0) {
            return ret;
        }
        int left = 0;
        int right = nums.length - 1;

        //计算出左端点
        while(left < right){
            int mid = left + (right - left)/2;
            if(nums[mid] < target){
                left = mid + 1;
            }else{
                right = mid;
            }
        }
        if(nums[left] != target){
            return ret;
        }else{
            ret[0] = left;
        }

        //计算右端点
        right = nums.length-1;
        while(left < right){
            int mid = left + (right - left + 1)/2;
            if(nums[mid] > target){
                right = mid - 1;
            }else{
                left = mid;
            }
        }
        ret[1] = left; 
        
        return ret;
    }
}

 这里先求出左端点要用素组存储，然后计算出右端点后再进行存储；

🚀2.2总结非朴素二分模版

查找左端点：

  while(left < right){
            int mid = left + (right - left)/2;
            if(......){
                left = mid + 1;
            }else{
                right = mid;
            }
        }

查找右端点：

   while(left < right){
            int mid = left + (right - left + 1)/2;
            if(.....){
                right = mid - 1;
            }else{
                left = mid;
            }
        }

注意了：

1.循环条件一直就是right > left

2.不知道是否是left + (right - left + 1)/2还是left + (right - left )/2;观察如果right = mid - 1，那么就是left + (right - left + 1)/2;如果right = mid，没有减去一，那么就是left + (right - left )/2;

📚️3.总结

本期小编主要讲解了关于二分查找的两种类型题目，从题目分析，算法分析，到代码编写逐步解析，最重要的还是对于朴素二分的细节处理，以及模版总结；