位运算

判定字符是否唯一

有很多解法,比如hash表,或者给字符串排个序,然后遍历…

写这道题时没注意到如果出现奇数个相同字符,此时就应该返回false了.
而不是全部放到位图中,最后再判断…

应该在放进去的时候就进行判断~

    public boolean isUnique(String astr) {
        int n = astr.length();
        if(n > 26) {
            return false;
        }
        
        int bit = 0;
        for(int i = 0; i < n; i++) {
            int m = astr.charAt(i)-'a';
            if(((bit >> m) & 1) == 0) {
                bit ^= 1 << m;
            } else {
                return false;
            }

        }

        return true;
    }

丢失的数字

直接秒了~

    public int missingNumber(int[] nums) {
        int n = nums.length;
        int sum = 0;
        for (int i = 0; i < n; i++) {
            sum ^= i;
            sum ^= nums[i];
        }
        sum ^= n;

        return sum;
    }

两整数之和

看这个讲解看懂了~ 两整数之和

    public int getSum(int a, int b) {
        while(b != 0) {
            // 进位
            int carry = (a & b) << 1;
            // 无符号相加
            a = a ^ b;

            // 最终结果 = carry(进位) + a(无符号相加结果) 
            // 因为不能使用 + ,所以再进入循环
            b = carry;
        }
        return a;
    }

只出现一次的数字 II

这个解法以前没见过,涨知识了~

这有个题解: 只出现一次的数字 II（有限状态自动机 + 位运算，清晰图解）

    public int singleNumber(int[] nums) {
        int ret = 0;
        for(int i=0;i<32;i++) {
            int sum = 0;
            for(int j=0;j<nums.length;j++) {
                sum += (nums[j] >> i) & 1;
            }
            ret += (sum%3)<<i;
        }
        return ret;
    }

消失的两个数字

这道题跟 只出现一次的数字 III 差不多.

坑:

• 找最后的结果时不仅要异或数组,还要异或 1 ~ n+2 的数字,如果想把这两个放到同一个循环内,那么要注意 它们俩的条件不同 !!

    public int[] missingTwo(int[] nums) {

        int sum = 0;
        int n = nums.length;
        for (int i = 0; i < n; i++) {
            sum ^= nums[i];
            sum ^= i + 1;
        }
        sum ^= n + 1;
        sum ^= n + 2;

        int p = sum & (-sum);
        int ret1 = 0;
        for (int i = 0; i < n; i++) {
            if ((nums[i] & p) == 0) {
                ret1 ^= nums[i];
            }
        }
        for (int i = 1; i <= n + 2; i++) {
            if ((i & p) == 0) {
                ret1 ^= i;
            }
        }
        int ret2 = sum ^ ret1;
        return new int[]{ret1, ret2};
    }

我找两个数的二进制的不同的那一位用的是 sum & (-sum)

题解用的跟我不一样,他是一位一位检查的~

    public int[] missingTwo(int[] nums) {

        int sum = 0;
        int n = nums.length;
        for (int i = 0; i < n; i++) {
            sum ^= nums[i];
            sum ^= i + 1;
        }
        sum ^= n + 1;
        sum ^= n + 2;

        int p = 0;
        while (true) {
            if (((sum >> p) & 1) == 1)
                break;
            else
                p++;
        }

        int ret1 = 0;
        for (int i = 0; i < n; i++) {
            if ((nums[i] & (1 << p)) == 0) {
                ret1 ^= nums[i];
            }
        }
        for (int i = 1; i <= n + 2; i++) {
            if ((i & (1 << p)) == 0) {
                ret1 ^= i;
            }
        }
        int ret2 = sum ^ ret1;
        return new int[]{ret1, ret2};
    }

常见位运算总结

1. 基础位运算

   • << 左移
   • >> 右移
   • ~ 按位取反. 记忆方法: 0 变 1, 1 变 0.
   • & 按位与. 记忆方法: 有 0 就是 0.
   • | 按位或. 记忆方法: 有 1 就是 1.
   • ^ 按位异或. 记忆方法: 相同为0,相异为一. 无进位相加.

2. 给一个数 n,确定它的二进制表示中的第 x 位是 0 还是 1.
   n = (n >> x) & 1

3. 将一个数 n 的二进制表示中的第 x 位修改成 1.
   n = n | ( 1 << x )

4. 将一个数 n 的二进制表示中的第 x 位修改成 0.
   n = n & ( ~ (1 << x) )

5. 位图

6. 提前一个数 n 的二进制表示中的最右侧的 1
   n & - n

   - n 的含义其实就是把 n 的二进制表示中的最右侧的 1 的左侧区域全部变成相反.
   我们都知道 - n = ~ n + 1
   

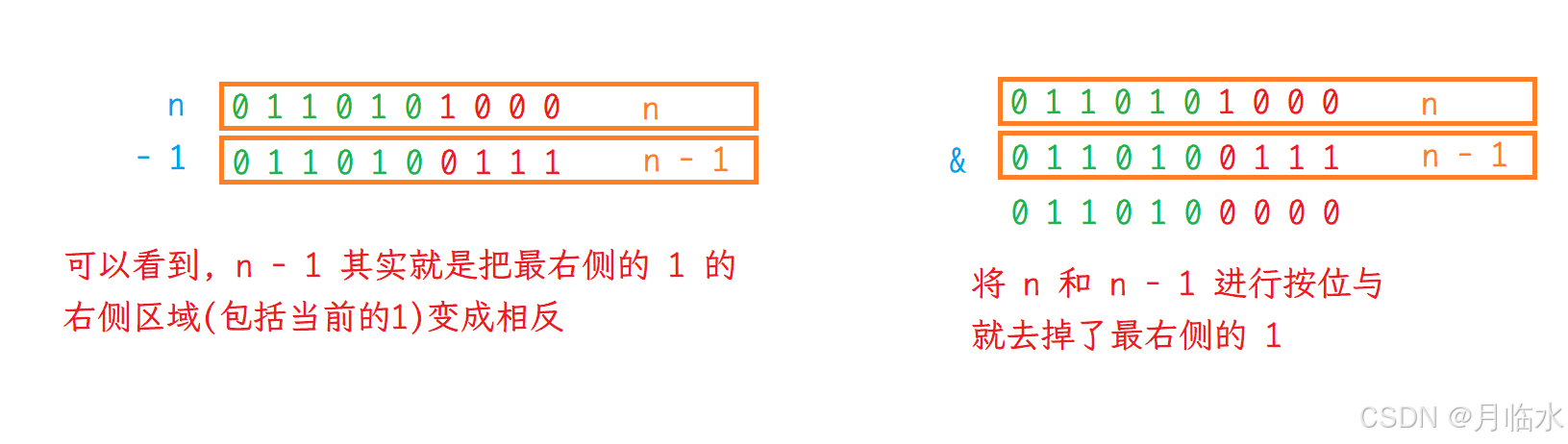
7. 干掉一个数 n 的二进制表示中最右侧的 1
   n & (n - 1)

   n - 1 其实是将 n 的二进制表示中的最右侧的 1 的右边区域(包括1) 全部变成相反
   

8. 位运算的优先级

   在使用时直接加括号,不要背优先级顺序 !!

9. 异或(^) 运算的运算律

   • a ^ 0 = a
   • a ^ a = 0 (消消乐)
   • a ^ b ^ c = a ^ (b ^ c)

练手题目:

1. 位 1 的个数
2. 比特位计数
3. 汉明距离
4. 只出现一次的数字
5. 只出现一次的数字 III