一、记忆化搜索vs动态规划
. - 力扣(LeetCode)

记忆化搜索:
class Solution {
public:
//记忆化搜索
//1、设置一个备忘录,要确保备忘录初始化的结果不能跟我们实际计算的结果相同
//2、添加备忘录,计算的时候,如果备忘录的位置是初始值,进行修改
//3、每次计算的时候,去备忘录瞅一瞅,找到的话,就可以不算了
int memory[31];
int fib(int n) {
memset(memory,-1,sizeof(memory)); //初始化成-1
return dfs(n);
}
int dfs(int n){
if(n<2) return n;
if(memory[n]!=-1) return memory[n];
memory[n]=dfs(n-1)+dfs(n-2);
return memory[n];
}
};动态规划:
class Solution {
public:
int fib(int n){
//改成动归
if(n<2) return n;
vector<int> dp(n+1);
dp[1]=1;
for(int i=2;i<=n;++i) dp[i]=dp[i-1]+dp[i-2];
return dp[n];
}
};动态规划优化滚动数组:
class Solution {
public:
int fib(int n) {
if (n < 2) return n;
int p = 0, q = 0, r = 1;
for (int i = 2; i <= n; ++i) {
p = q;
q = r;
r = p + q;
}
return r;
}
};
二、不同路径
62. 不同路径 - 力扣(LeetCode)
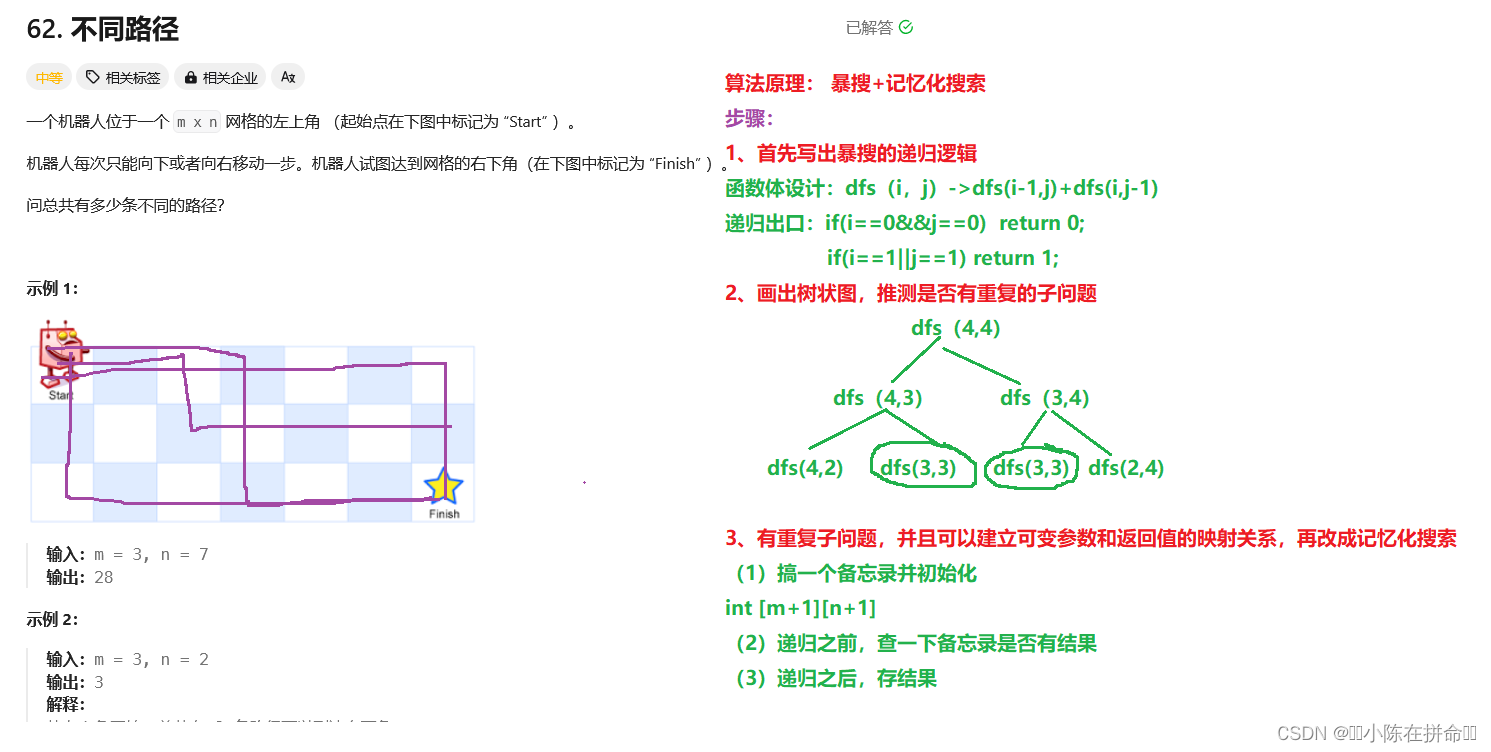
记忆化搜索:
class Solution {
public:
int uniquePaths(int m, int n) {
//dfs(i,j) =dp(i-1,j)+dp(i,j-1)
vector<vector<int>> memory(m,vector<int>(n,-1));
return dfs(m-1,n-1,memory);
}
int dfs(int i,int j,vector<vector<int>>&memory)
{
if(i<0||j<0) return 0;
if(i==0&&j==0) return 1;
if(memory[i][j]!=-1) return memory[i][j];
memory[i][j]=dfs(i-1,j,memory)+dfs(i,j-1,memory);
return memory[i][j];
}
};动态规划:
class Solution {
public:
int uniquePaths(int m, int n)
{
vector<vector<int>> dp(m+1,vector<int>(n+1));//创建一个dp数组
//初始化dp[0][1]
dp[0][1]=1;
//开始填表
for(int i=1;i<=m;++i)
for(int j=1;j<=n;++j)
dp[i][j]=dp[i-1][j]+dp[i][j-1];
return dp[m][n];
}
};动态规划优化滚动数组:
class Solution {
public:
int uniquePaths(int m, int n) {
vector<int> dp(n + 1); // 创建一个dp数组
dp[1] = 1;
// 开始填表
for (int i = 1; i <= m; ++i)
for (int j = 1; j <= n; ++j)
dp[j] += dp[j - 1];
return dp[n];
}
};三、最长的递增子序列
300. 最长递增子序列 - 力扣(LeetCode)
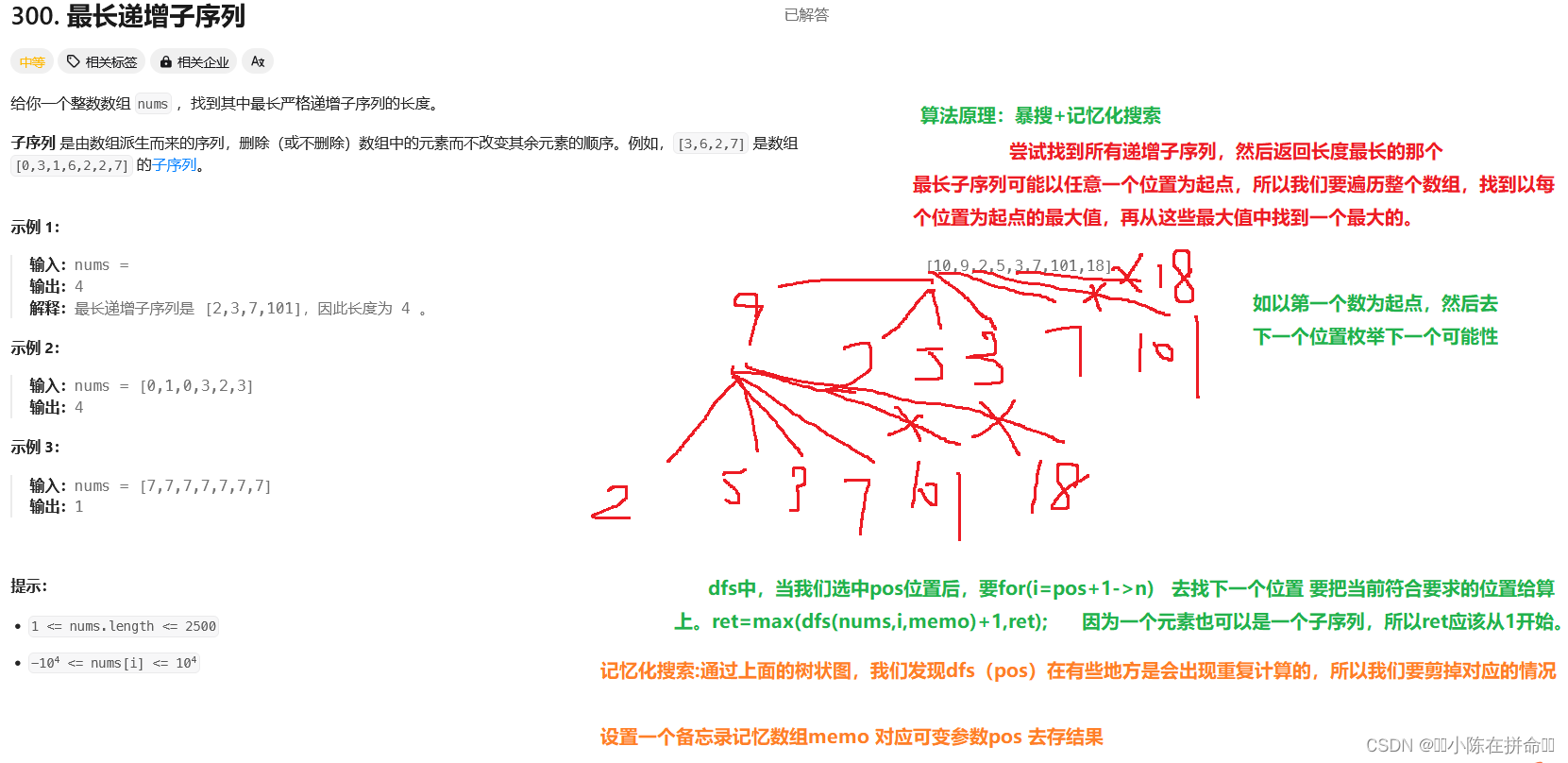
记忆化搜索:
class Solution {
public:
//记忆化搜索
//不用记忆化搜索的话会超时,因为本身就是一个多叉树
int n;
int lengthOfLIS(vector<int>& nums) {
n=nums.size();
vector<int> memory(n);
int ret=1;
for(int i=0;i<n;++i) ret=max(dfs(nums,i,memory),ret);
return ret;
}
int dfs(vector<int>& nums,int pos,vector<int>&memory){ //帮我们返回以pos位置为起点的最长递增子序列
if(memory[pos]) return memory[pos];
int ret=1;
for(int i=pos+1;i<n;++i)
if(nums[i]>nums[pos]) ret=max(dfs(nums,i,memory)+1,ret);
return memory[pos]=ret;
}
};动态规划:
class Solution {
public:
//记忆化搜索改动归 以i结尾时的最长递增子序列 nums[j]<nums[i]时dp[i]=max(dp[i-j]+1)
int lengthOfLIS(vector<int>& nums) {
int n=nums.size();
vector<int> dp(n,1);
for(int i=1;i<n;++i)
for(int j=0;j<i;++j)
if(nums[j]<nums[i]) dp[i]=max(dp[j]+1,dp[i]);
return*max_element(dp.begin(), dp.end());
}
};四、猜数字大小II
375. 猜数字大小 II - 力扣(LeetCode)
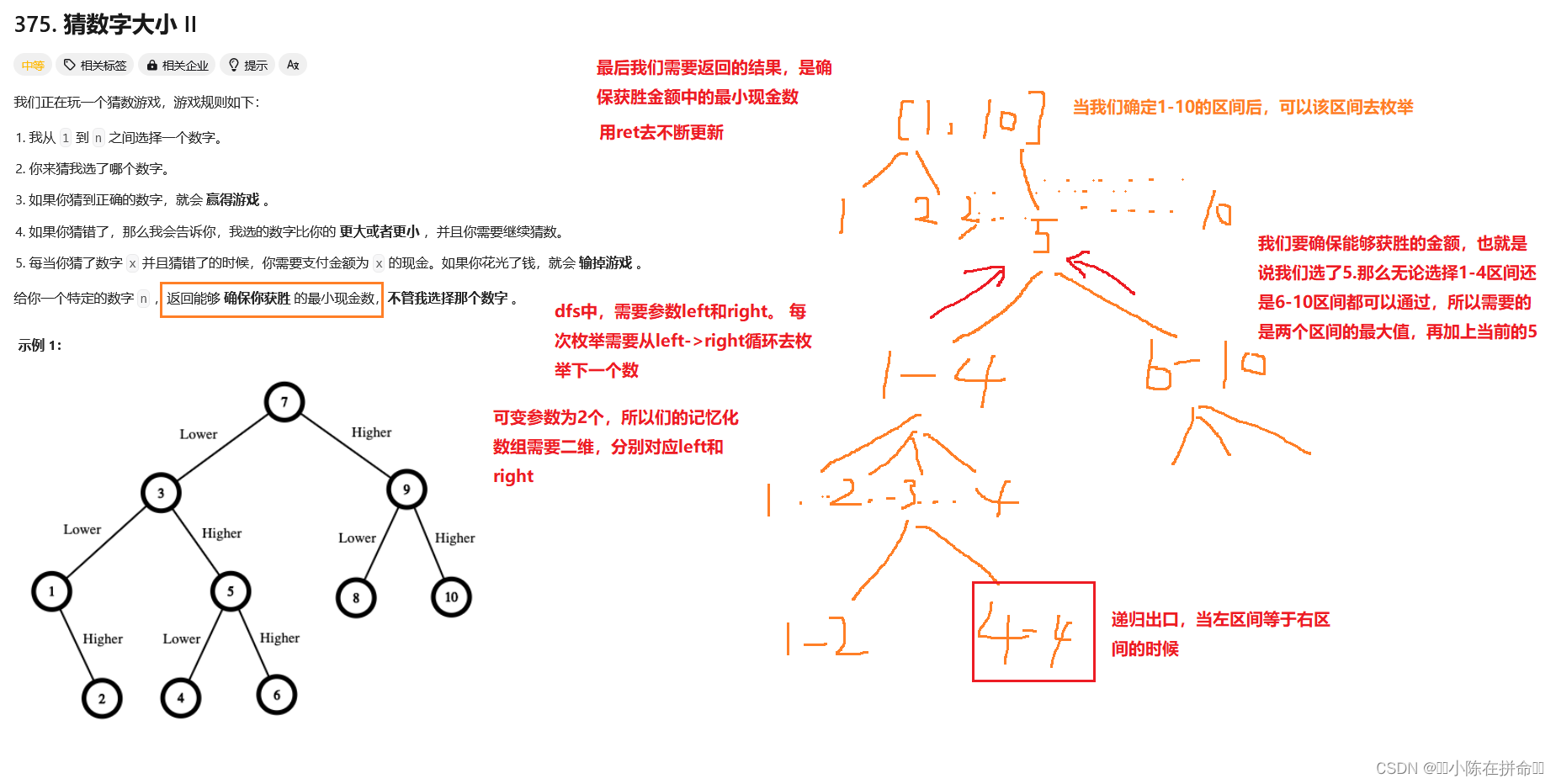
记忆化搜索:
class Solution {
public:
int getMoneyAmount(int n) {
vector<vector<int>> memory(n+1,vector<int>(n+1));//边界才会为0 所以不需要初始化为-1
return dfs(1,n,memory);
}
int dfs(int left,int right,vector<vector<int>>&memory){
if(left>=right) return 0;//边界情况才为0
if(memory[left][right]) return memory[left][right];//说明不是第一次进来了
int ret=INT_MAX;
for(int i=left;i<=right;++i){ //尝试去选1-10
int l=dfs(left,i-1,memory);
int r=dfs(i+1,right,memory);
ret=min(ret,max(l,r)+i);
}
return memory[left][right]=ret;
}
};动态规划:
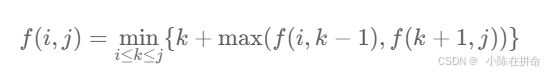
class Solution {
public:
int getMoneyAmount(int n) {
//dp[i][j]表示[i,j]内确保胜利的最小金额 我们要求的是dp[1][n]
//假设第一次猜x dp[1][n]=x+max(dp[1][x-1],dp[x+1][n]) i>=j时 dp[i][j]=0
//如果在i j范围内选择了k 那么dp[i][j]=k+max(f(i,k−1),f(k+1,j))
//然后我们要遍历i-j内所有k的可能 找到其中最小的那个
vector<vector<int>> dp(n+1,vector<int>(n+1));
for(int i=n-1;i>=1;--i) //dp[1][n] 要从做下角往右上角填
for(int j=i+1;j<=n;++j){
dp[i][j]=j+dp[i][j-1];//把边界领出来
for(int k=i;k<j;++k) //k-1不会越界 但是k+1会越界!!
dp[i][j]=min(dp[i][j],k+max(dp[i][k-1],dp[k+1][j]));
}
return dp[1][n];
}
};五、矩阵的最长递增路径
329. 矩阵中的最长递增路径 - 力扣(LeetCode)
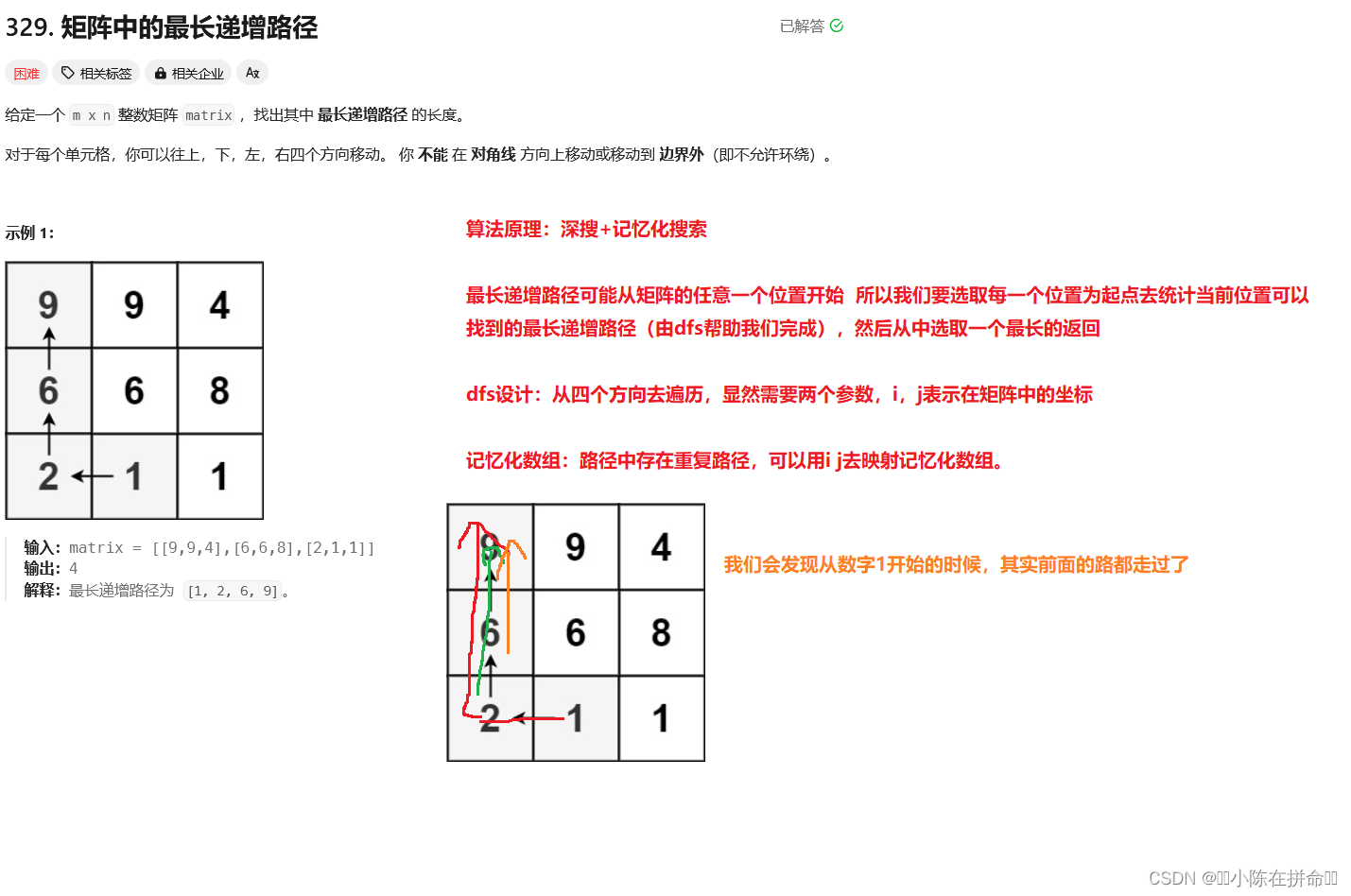
class Solution {
public:
int m,n;
int longestIncreasingPath(vector<vector<int>>& nums) {
m=nums.size(),n=nums[0].size();
vector<vector<int>> memory(m,vector<int>(n));
int ret=1;
for(int i=0;i<m;++i)
for(int j=0;j<n;++j)
ret=max(ret,dfs(nums,i,j,memory));//以任意位置为起点 dfs帮我们去找
return ret;
}
int dx[4]={-1,1,0,0};
int dy[4]={0,0,-1,1};
int dfs(vector<vector<int>>& nums,int i,int j,vector<vector<int>>& memory){
if(memory[i][j]) return memory[i][j];
int ret=1;
for(int k=0;k<4;++k){
int x=dx[k]+i,y=dy[k]+j;
if(x>=0&&x<m&&y>=0&&y<n&&nums[x][y]>nums[i][j])
ret=max(ret,dfs(nums,x,y,memory)+1);
}
return memory[i][j]=ret;
}
};六、分割回文串
131. 分割回文串 - 力扣(LeetCode)

动归预处理+回溯
class Solution {
public:
vector<vector<string>> ret;//记录返回结果
vector<string> path;//记录路径
vector<vector<bool>> dp;//预处理的dp数组
int n;
vector<vector<string>> partition(string&s) {
n=s.size();
//先用dp数组进行预处理
dp.resize(n,vector<bool>(n));
for(int i=n-1;i>=0;--i)
for(int j=i;j<n;++j)
if(s[i]==s[j]) dp[i][j]=i+1<j?dp[i+1][j-1]:true;
dfs(s,0); //以i位置为起点 去帮我们确认哪些是回文子串
return ret;
}
void dfs(string&s,int i)
{
if(i==n) ret.emplace_back(path);
for(int j=i;j<n;++j)
if(dp[i][j]) {
path.emplace_back(s.substr(i,j-i+1));
dfs(s,j+1);
path.pop_back();
}
}
};记忆化搜索+回溯
class Solution {
public:
vector<vector<int>> memory;//记忆化数组 -1表示非回文 0表示未搜索 1表示是回文
vector<vector<string>> ret;
vector<string> path;
int n;
vector<vector<string>> partition(string&s) {
n=s.size();
memory.resize(n,vector<int>(n));
dfs(s,0);
return ret;
}
void dfs(string&s,int i){
if(i==n) ret.emplace_back(path);
for(int j=i;j<n;++j)
if(ispal(s,i,j)==1) {
path.emplace_back(s.substr(i,j-i+1));
dfs(s,j+1);
path.pop_back();
}
}
int ispal(const string&s,int i,int j)
{
if(memory[i][j]) return memory[i][j];//如果是-1或者1 就直接返回
if(s[i]!=s[j]) return memory[i][j]=-1;
return memory[i][j]=i+1<j?ispal(s,i+1,j-1):1;
}
};
