852. 山脉数组的峰顶索引
题目:
给定一个长度为
n的整数 山脉 数组arr,其中的值递增到一个 峰值元素 然后递减。返回峰值元素的下标。
你必须设计并实现时间复杂度为
O(log(n))的解决方案。
示例 1:
输入:arr = [0,1,0] 输出:1示例 2:
输入:arr = [0,2,1,0] 输出:1示例 3:
输入:arr = [0,10,5,2] 输出:1提示:
3 <= arr.length <= 1050 <= arr[i] <= 106- 题目数据 保证
arr是一个山脉数组
思路:题目就是让我们找出数组中的最大值。暴力枚举应该是非常容易想到的。
代码实现:
暴力枚举:
class Solution {
public int peakIndexInMountainArray(int[] arr) {
// 遍历数组寻找最大值
int max = 0;
for (int i = 1; i < arr.length; i++) {
if (arr[i] > arr[max]) {
max = i;
} else { // max此时就是最大值
break;
}
}
return max;
}
}我们仔细观察会发现数组有一个特点:先是按照严格的升序排列,再是按照严格的降序排列。这也就是我们所说的二段性,即可以使用二分查找算法来解决问题。
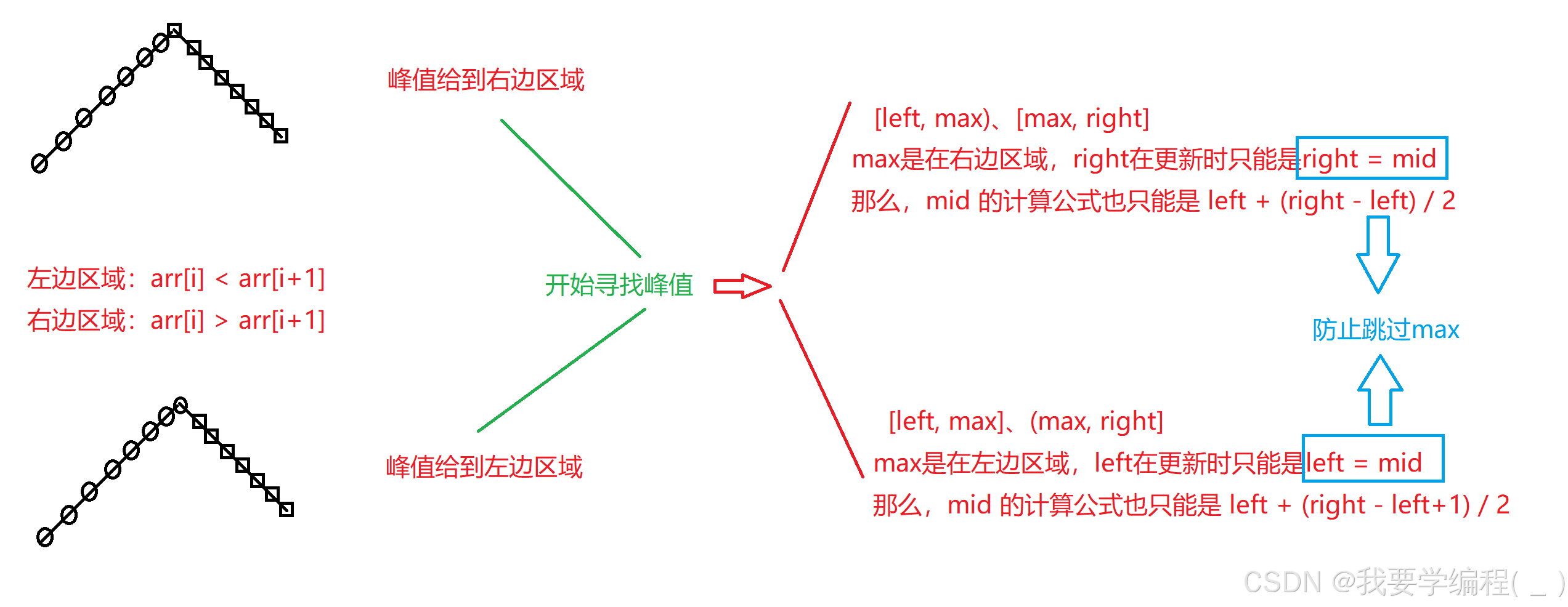
代码实现:
峰值在右边区域:
class Solution {
public int peakIndexInMountainArray(int[] arr) {
// 二分查找寻找峰值
int left = 1;
int right = arr.length-2;
while (left < right) {
int mid = left + (right - left) / 2;
// 峰值存在于右边区间,因此只能和右区间进行比较,而不能跑到左边区间去
if (arr[mid] < arr[mid+1]) {
// 落在左边区域
left = mid+1;
} else {
// 落在右边区域
right = mid;
}
}
return left;
}
}峰值在左边区域:
class Solution {
public int peakIndexInMountainArray(int[] arr) {
// 二分查找寻找峰值
int left = 1;
int right = arr.length-2;
while (left < right) {
int mid = left + (right - left + 1) / 2;
// 峰值存在于左边区间,因此只能和左边区间进行比较,而不能跑到右边区间去
if (arr[mid-1] < arr[mid]) {
// 落在左边区域
left = mid;
} else {
// 落在右边区域
right = mid-1;
}
}
return left;
}
}注意:
1、由于题目说了,数组长度是大于等于3并且一定存在峰值的,因此第一个元素和最后一个元素肯定不是峰值。
2、在比较时,一定要清楚我们是将峰值分在哪个区域,继而再进行正确的分值(left、right、mid)和比较。
162. 寻找峰值
题目:
峰值元素是指其值严格大于左右相邻值的元素。
给你一个整数数组
nums,找到峰值元素并返回其索引。数组可能包含多个峰值,在这种情况下,返回 任何一个峰值 所在位置即可。你可以假设
nums[-1] = nums[n] = -∞。你必须实现时间复杂度为
O(log n)的算法来解决此问题。
示例 1:
输入:nums = [1,2,3,1] 输出:2 解释:3 是峰值元素,你的函数应该返回其索引 2。示例 2:
输入:nums = [1,2,1,3,5,6,4] 输出:1 或 5 解释:你的函数可以返回索引 1,其峰值元素为 2; 或者返回索引 5, 其峰值元素为 6。提示:
1 <= nums.length <= 1000-231 <= nums[i] <= 231 - 1- 对于所有有效的
i都有nums[i] != nums[i + 1]
思路:题目让我们随机找到一个严格大于左右两边的峰值元素即可。暴力枚举的做法也是很轻易能够想到的。
代码实现:
暴力枚举:
class Solution {
public int findPeakElement(int[] nums) {
// 找到严格大于左右元素即可
int max = -1;
for (int i = 0; i < nums.length; i++) {
if (i-1 < 0) { // 只需判断右边的
if (i+1 >= nums.length) {
max = 0; // 当只有一个元素时
break;
} else {
if (nums[i] > nums[i+1]) {
max = i;
break;
}
}
} else { // 只需判断右边
if (i+1 >= nums.length) {
// 判断左边
if (nums[i-1] < nums[i]) {
max = i;
break;
}
} else {
// 判断两边
if (nums[i] > nums[i-1] && nums[i] > nums[i+1]) {
max = i;
break;
}
}
}
}
return max;
}
}由于题目只需要让我们随机返回一个峰值即可,因此只要是找到符合要求的就不需要再遍历数组了。
由于题目要求我们应使用时间复杂度为log N的算法来解决,因此这里我们联想到二分查找算法。
那有小伙伴可能会有疑惑:二分查找不是只适用于有序的数据的情况下吗?
认识二分查找算法的二段性:
1、有一个条件将数组可以分成两部分。
例如:在一个有序数组中查找某个元素是否存在。
1 2 3 4 5 6 7 8
找到中间值mid,将数组分成两部分:一部分全部大于等于mid,一部分全部小于mid。
这里就是利用一个条件将数组分成了两部分。
而在本题中:找到中间值mid,根据-∞到mid和mid+1的特性(下面的图片所示),将数组分为两部分:
一部分,肯定存在峰值;一部分,可能存在峰值。 ----> 二段性。2、确定二分查找的中间值取法、left与right的取法(可以去看第一篇关于二分查找的博客)
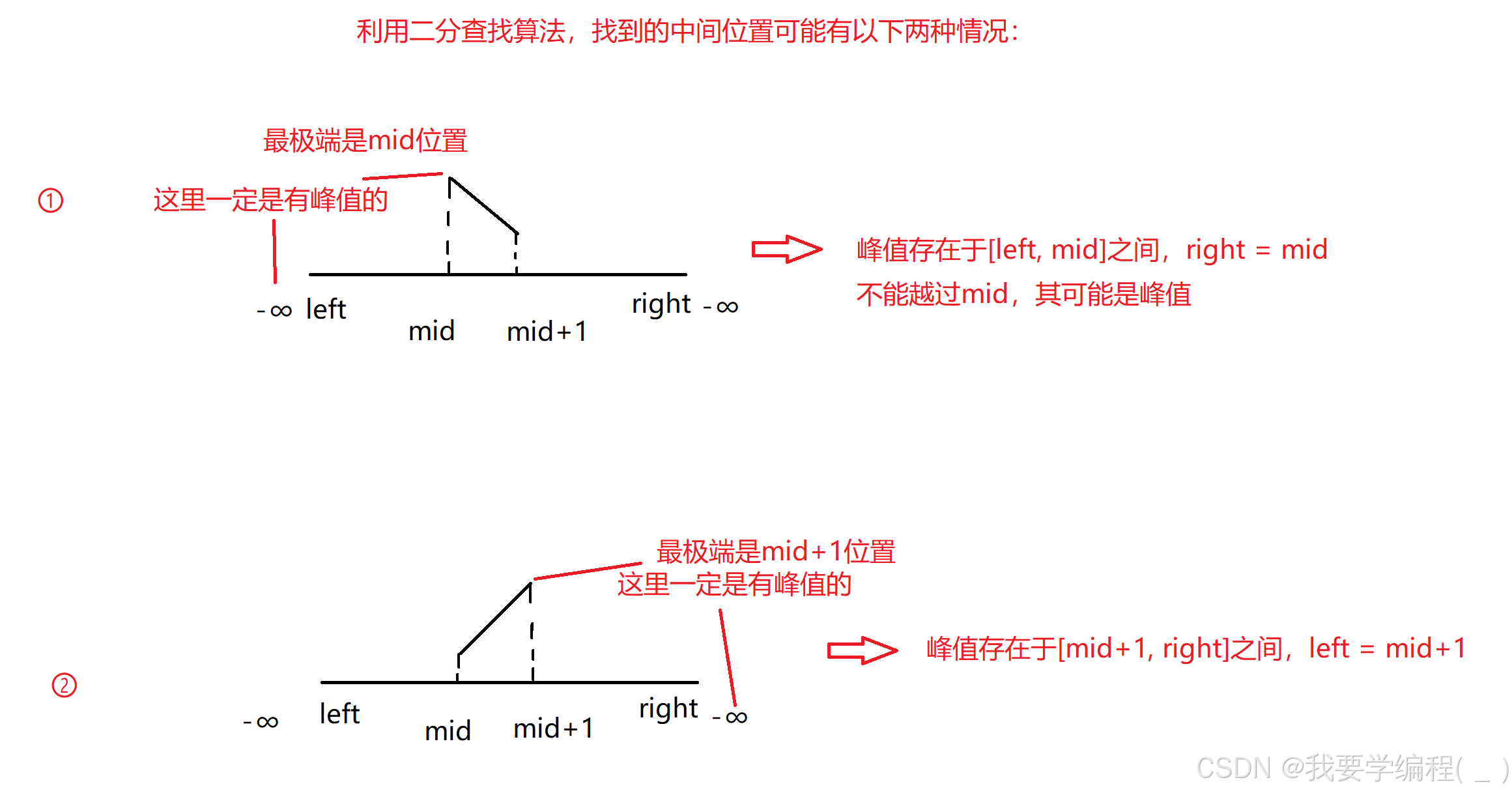
因此,我们确定一个题目是否可以使用二分查找算法来解决的前提是:我们可以找到一个条件,将数组划分为两部分,即确定数组是否存在二段性。而这个二段性则是最难发现的。
代码实现:
class Solution {
public int findPeakElement(int[] nums) {
int left = 0;
int right = nums.length-1;
while (left < right) {
int mid = left + (right-left) / 2;
if (nums[mid] > nums[mid+1]) {
right = mid;
} else {
left = mid+1;
}
}
return left; // 也可以是right
}
}当然上面是拿 mid 和 mid+1进行比较,也可以拿 mid-1 和 mid 进行比较
class Solution {
public int findPeakElement(int[] nums) {
int left = 0;
int right = nums.length-1;
while (left < right) {
int mid = left + (right-left+1) / 2;
if (nums[mid-1] < nums[mid]) {
left = mid;
} else {
right = mid-1;
}
}
return left; // 也可以是right
}
}代码总体实现的功能是一样的,只是细节的处理和站的角度不同而已。
这里我们看出,二分查找重在思想(怎么找到二段性),代码的实现是非常简单的。 并且我们也知道了二分查找并不是只适用于有序的数据了。
153. 寻找旋转排序数组中的最小值
题目:
已知一个长度为
n的数组,预先按照升序排列,经由1到n次 旋转 后,得到输入数组。例如,原数组nums = [0,1,2,4,5,6,7]在变化后可能得到:
- 若旋转
4次,则可以得到[4,5,6,7,0,1,2]- 若旋转
7次,则可以得到[0,1,2,4,5,6,7]注意,数组
[a[0], a[1], a[2], ..., a[n-1]]旋转一次 的结果为数组[a[n-1], a[0], a[1], a[2], ..., a[n-2]]。给你一个元素值 互不相同 的数组
nums,它原来是一个升序排列的数组,并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。你必须设计一个时间复杂度为
O(log n)的算法解决此问题。
示例 1:
输入:nums = [3,4,5,1,2] 输出:1 解释:原数组为 [1,2,3,4,5] ,旋转 3 次得到输入数组。示例 2:
输入:nums = [4,5,6,7,0,1,2] 输出:0 解释:原数组为 [0,1,2,4,5,6,7] ,旋转 3 次得到输入数组。示例 3:
输入:nums = [11,13,15,17] 输出:11 解释:原数组为 [11,13,15,17] ,旋转 4 次得到输入数组。提示:
n == nums.length1 <= n <= 5000-5000 <= nums[i] <= 5000nums中的所有整数 互不相同nums原来是一个升序排序的数组,并进行了1至n次旋转
思路:题目罗里吧嗦地说了一大推其实就是在一个旋转数组中求最小值的问题。直接遍历即可。
代码实现:
暴力枚举:
class Solution {
public int findMin(int[] nums) {
int min = nums[0];
for (int i = 1; i < nums.length; i++) {
if (nums[i] < min) {
min = nums[i];
}
}
return min;
}
}这个暴力枚举,简直就是初学C语言的语法题,不能算是算法题。
根据题目所说的 log N 的时间复杂度,就应该联想到使用二分查找的思路。
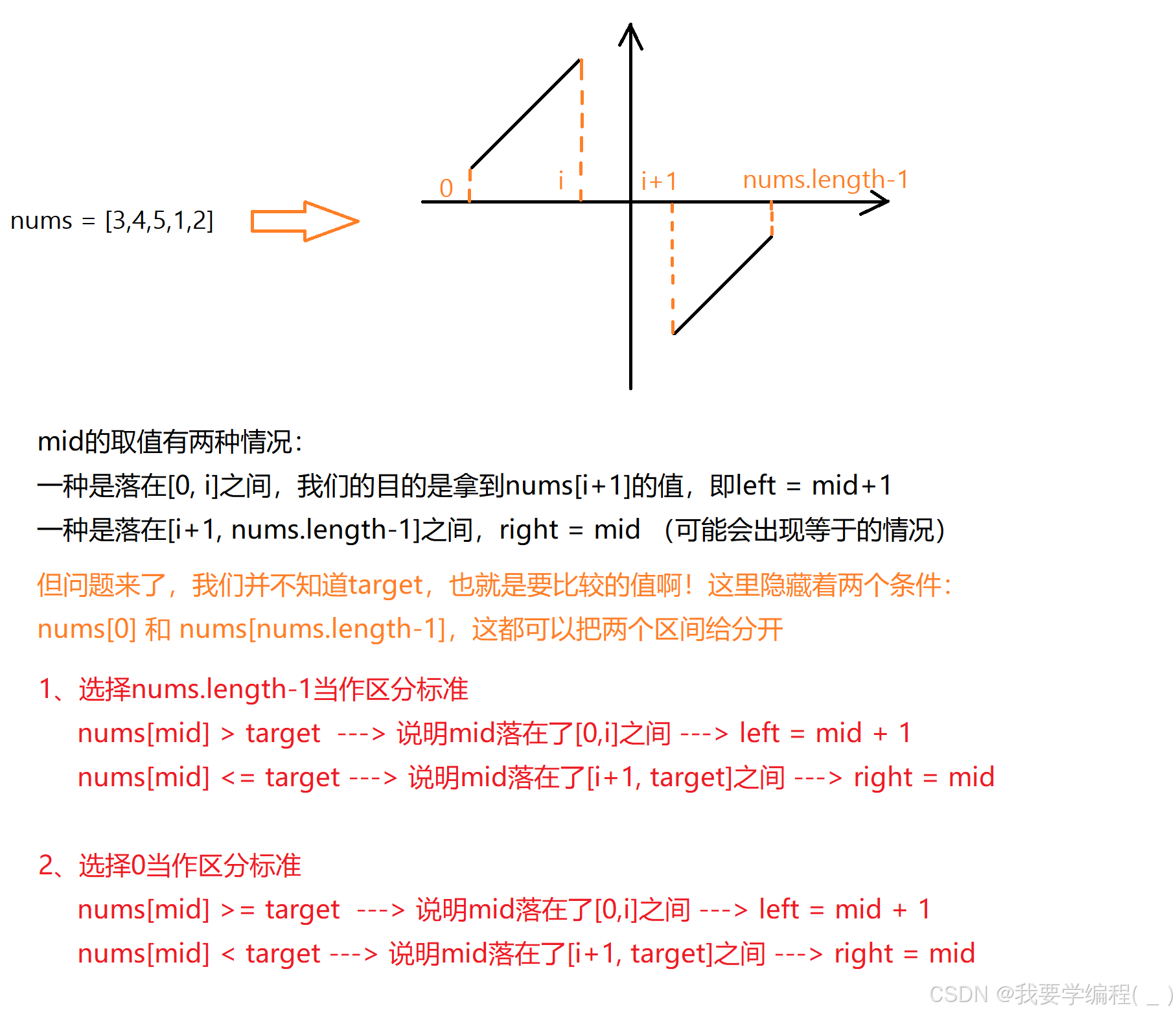
1、选择 nums.length-1当作区分标准:
class Solution {
public int findMin(int[] nums) {
int left = 0;
int right = nums.length-1;
// 选择nums.length-1当作标准
int target = nums[nums.length-1];
while (left < right) {
int mid = left + (right-left) / 2;
if (nums[mid] > target) {
left = mid+1;
} else {
right = mid;
}
}
return nums[left];
}
}2、选择 0 当作区分标准:
class Solution {
public int findMin(int[] nums) {
int left = 0;
int right = nums.length-1;
// 选择0当作标准
int target = nums[0];
while (left < right) { // 这个只适合有断层的数据
int mid = left + (right-left) / 2;
if (nums[mid] >= target) {
left = mid+1;
} else {
right = mid;
}
}
// 当数组本身是有序时,上面的方法不适合。得特判一下
return nums[left] > nums[0] ? nums[0] : nums[left];
}
}LCR. 173.点名
题目:
某班级 n 位同学的学号为 0 ~ n-1。点名结果记录于升序数组
records。假定仅有一位同学缺席,请返回他的学号。
示例 1:
输入: records = [0,1,2,3,5] 输出: 4示例 2:
输入: records = [0, 1, 2, 3, 4, 5, 6, 8] 输出: 7提示:
1 <= records.length <= 10000
思路:
总共有五种解法:
1、哈希表
用一个数组模拟哈希表去记录 records 数组中的元素,接着再遍历哈希表,找出其中值为0的下标
代码实现:
class Solution {
// 哈希表
public int takeAttendance(int[] records) {
int n = records.length;
int[] hash = new int[n+1]; // 要多申请一个空间
for (int i = 0; i < records.length; i++) {
hash[records[i]]++;
}
// 值为0的就是丢失的数字
int num = 0;
// 这里要遍历哈希表
for (int i = 0; i < hash.length; i++) {
if (hash[i] == 0) {
num = i;
}
}
return num;
}
}2、位运算
利用异或运算符的特性(相同的数异或为0)去查找丢失的数字。
代码实现:
class Solution {
// 位运算
public int takeAttendance(int[] records) {
int n = records.length;
int num = 0;
for (int i = 0; i < n; i++) {
num ^= (records[i] ^ i);
}
return num ^ n;
}
}3、直接遍历查找
直接遍历数组,查找丢失的数字
代码实现:
class Solution {
// 直接遍历查找
public int takeAttendance3(int[] records) {
int n = records.length;
int num = -1; // 取0可能会误判
for (int i = 0; i < n; i++) {
if (records[i] != i) {
num = i;
break;
}
}
// 排除特殊情况
return num == -1 ? n : num;
}
}注意:
1、当数组处于 [0,1,2,3,4] 这种有序的状态时, 缺少的 n 是循环查找不出来的,因此得去进行特殊处理。
2、当数组处于 [1,2,3,4] 这种状态时,如果 num 初始化为 0,那么更新之后的结果还是 0,容易和上面一种情况混淆,因此 num 的初始值只能是负数。
4、数学方法(高斯求和、等差数列的求和)
将数组的值全部加起来再减去对应的下标,最后再加上数组的长度,得到的就是丢失的数字
代码实现:
class Solution {
// 高斯求和
public int takeAttendance(int[] records) {
int sum = 0;
int i = 0;
for (; i < records.length; i++) {
sum += (i-records[i]);
}
sum += i;
return sum;
}
}上面方法都可以通过题目测试,但是时间复杂度还是不少的,不是最优解法。
5、二分查找
在直接遍历查找的过程中,是直接去从头开始遍历,会将一些无效的数据也查找一遍。因此可以尝试用二分查找来优化。首先,二分查找得找到数据的二段性。

代码实现:
class Solution {
// 二分查找
public int takeAttendance(int[] records) {
int left = 0;
int right = records.length-1;
while (left < right) {
int mid = left + (right-left) / 2;
if (records[mid] == mid) {
left = mid+1;
} else {
right = mid;
}
}
// 也要特判
return left == records[left] ? left+1 : left;
}
}注意:因为二分查找 是对 暴力枚举的优化,因此也要避免 有序数组的情况。(二分查找只是优化在查找效率上面,其余的和暴力枚举没啥区别)
以上就是 关于二分查找的 经典题目集合了,相信通过这篇文章,咱们以后遇到二分的题目,肯定能AC的(但首先得找到二段性,这个过程是比较难的)。
好啦!本期 二分查找算法专题(2)的学习之旅 就到此结束啦!我们下一期再一起学习吧!

