前言

什么是路径规划

路径规划是指在一个给定的环境中，找到一条从起点到终点的有效路径，同时避免遇到障碍物和满足一定的优化条件，如最短距离、最低能耗、最快时间等。

应用场景
机器人导航：在工业、服务或探测机器人中，路径规划帮助机器人有效避开障碍物，到达目的地。
自动驾驶汽车：自动驾驶汽车需要实时路径规划来选择最佳路线，同时遵守交通规则和避免碰撞。
无人机飞行：无人机在执行任务时，路径规划可以帮助其避开建筑物、山脉等障碍，并优化飞行路径。
物流与运输：在物流行业中，路径规划用于优化配送路线，减少运输成本和时间。
网络路由：在计算机网络中，数据包的路由也需要进行路径规划，以确保数据高效、安全地传输。

路径规划通常涉及以下几种方法：
图搜索算法：如Dijkstra算法、A算法、D算法等，它们在图中寻找最短路径。
采样方法：如RRT（快速随机树）、PRM（概率路线图）等，它们通过随机采样来构建可行路径。
基于模型的方法：这种方法会建立一个环境的模型，然后在该模型上规划路径。
机器学习方法：近年来，深度学习等机器学习方法也被用于路径规划，尤其是对于复杂环境。
路径规划是一个不断发展的领域，随着技术的进步，将会出现更多高效、智能的规划方法。

在学习该算法之前，我们要了解什么是最短路径，该算法是求最短路径的一个方法。

1.什么是最短路径

最短路径（Shortest Path）是指在加权图中，从起点到终点经过的路径中，边的权重之和最小的那条路径。在不同的应用场景中，权重可以代表距离、时间、成本、能耗等不同的度量。
以下是最短路径的一些关键特点：
图的结构：最短路径问题通常在一个图（Graph）上进行研究，图由节点（Vertices）和连接节点的边（Edges）组成。边可以是有向的或无向的，并且可以带有权重。
权重：每条边都有一个权重，表示从一个节点到另一个节点的“代价”。最短路径问题就是在所有可能的路径中找到总权重最小的路径。
单源最短路径：从一个特定的起点到图中所有其他节点的最短路径。例如，Dijkstra算法和Bellman-Ford算法可以解决单源最短路径问题。
所有节点对最短路径：找出图中每一对节点之间的最短路径。Floyd-Warshall算法是解决所有节点对最短路径问题的算法之一。
无权图：在无权图中，最短路径问题简化为找到从起点到终点的最少边数路径，这可以通过广度优先搜索（Breadth-First Search, BFS）算法来解决。
算法：有多种算法可以用来寻找最短路径，包括但不限于Dijkstra算法、Bellman-Ford算法、Floyd-Warshall算法和A*算法。
应用：最短路径问题在现实世界中有着广泛的应用，例如在地图导航、网络路由、交通规划、物流配送等领域。

举例来说，如果你需要从家出发去一个公园，最短路径问题就是要找到从你家到公园的最短路程，这通常是通过考虑所有可能的路线，并选择总路程（权重之和）最短的那条路线来实现的。 

2. Dijkstra算法

Dijkstra算法是一种著名的图搜索算法，用于在加权图中找到从单一源点出发到所有其他节点的最短路径。该算法由荷兰计算机科学家艾兹赫尔·戴克斯特拉（Edsger W. Dijkstra）在1959年提出，是解决单源最短路径问题的经典算法之一。
算法基本原理
Dijkstra算法基于贪心策略，它每次都选择当前未处理节点中距离源点最近的节点，然后更新从这个节点出发到其邻接节点的最短路径长度。这个过程一直重复，直到所有节点的最短路径都被找到。

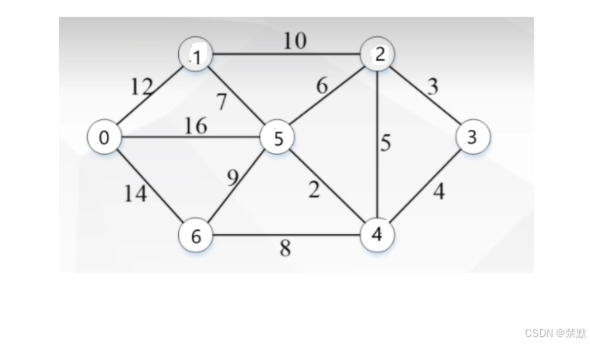
数学图形模型展示（b站上找的课件图片）

 

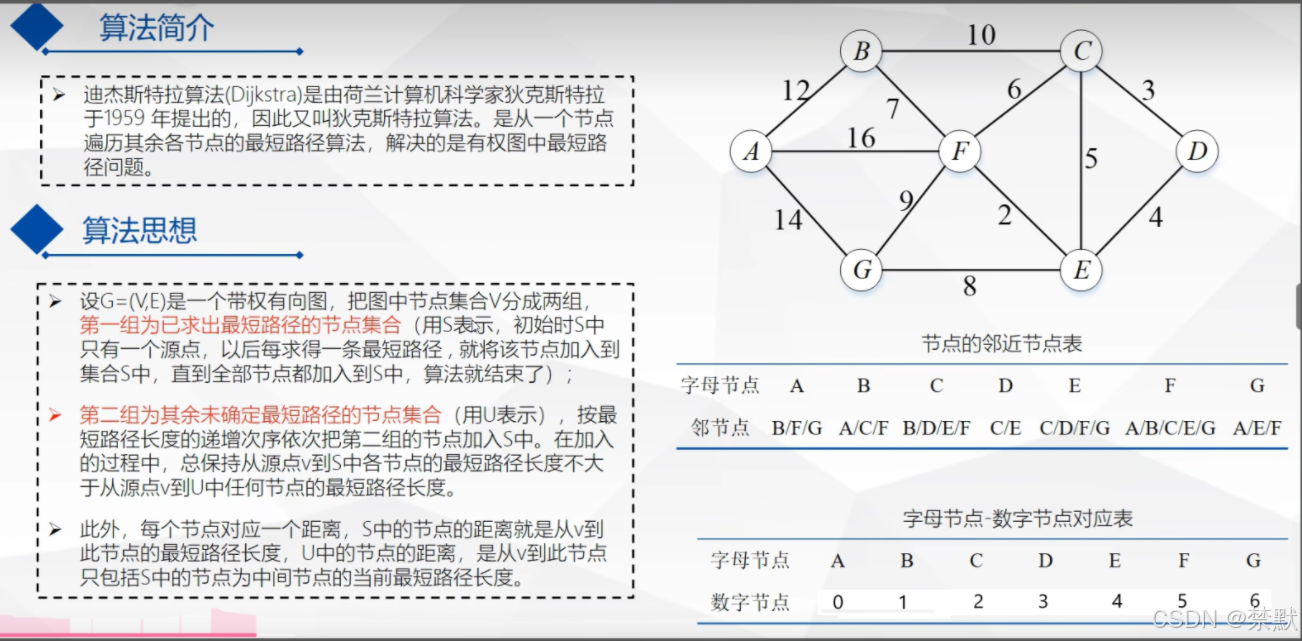
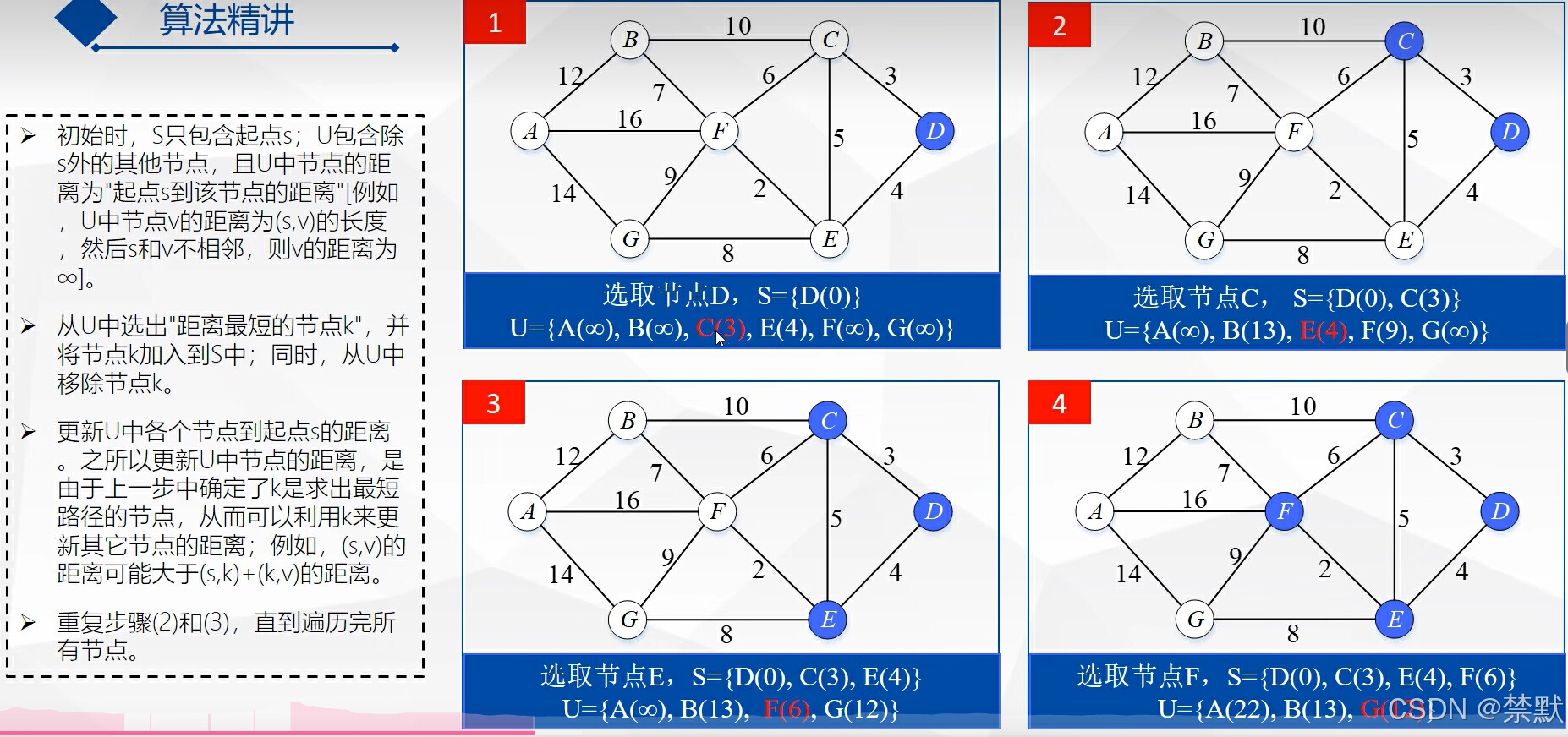
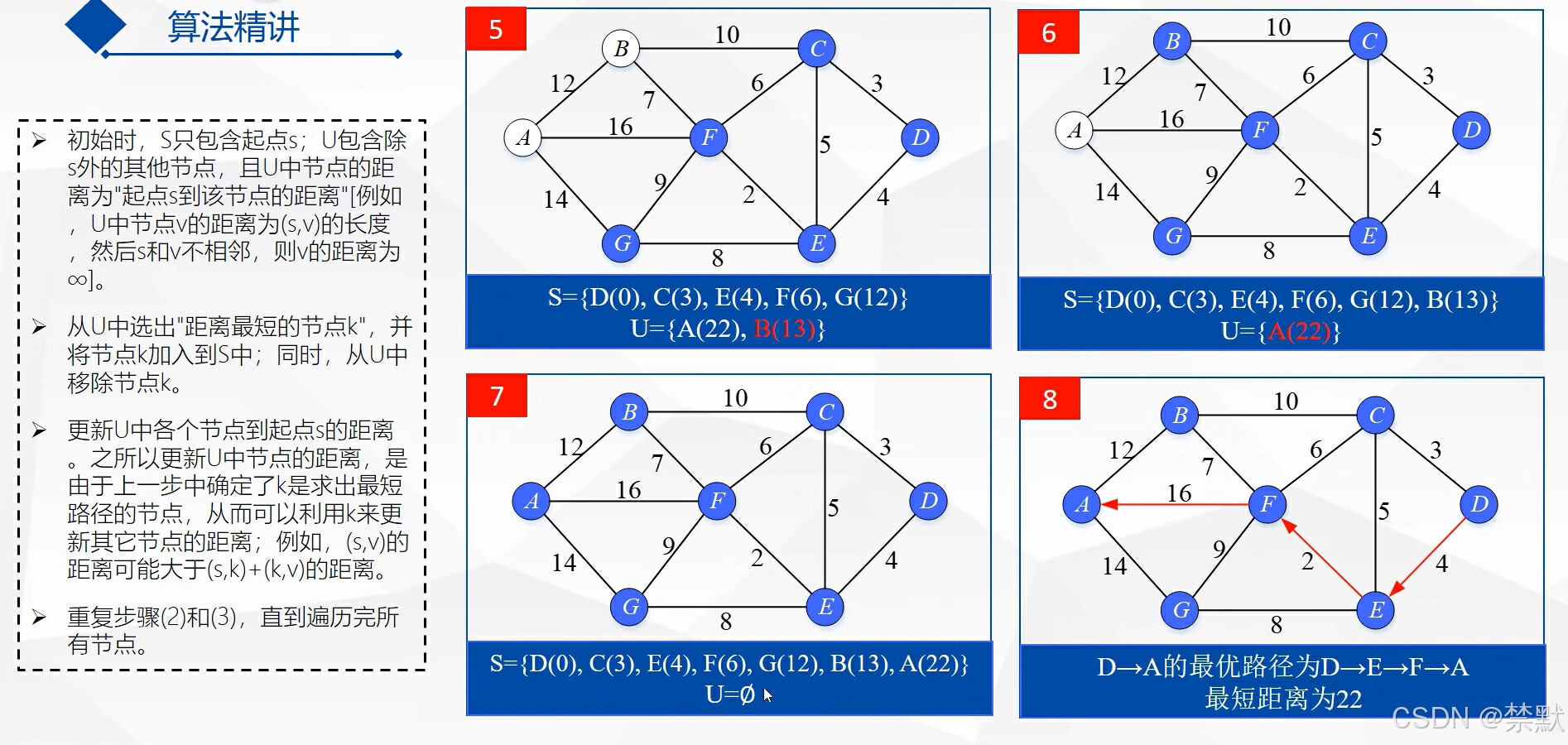
算法步骤

以下是Dijkstra算法的步骤（方便叙述，将数组和函数都说了对应名字）

• 初始化：

  • 创建一个数组 例如 dist[] 来存储源点到每个节点的最短距离，所有节点的距离初始化为无穷大（INF），源点的距离设置为0。
  • 创建一个数组 sptSet[]，用于标记哪些节点已经被处理（即已确定最短路径）。
  • 选择一个源点，首先将源点的距离设置为0，其它节点的距离保持为无穷大。

• 选择距离最小的未处理节点：

  • 在每一步中，从尚未处理的节点中选择一个距离最小的节点（即最短路径的节点）。这一步通过 minDistance 函数实现。

• 更新邻接节点的距离：

  • 对于当前选中的节点，遍历它所有的邻接节点，检查通过当前节点是否可以找到更短的路径。如果是，就更新邻接节点的最短距离。

• 重复过程：

  • 重复步骤2和步骤3，直到所有节点都被处理完毕。每次都会选出一个新的节点并更新它的邻接节点。

• 结束：

  • 当所有节点的最短路径都被确定（即 sptSet[] 中所有节点都标记为已处理），算法结束。此时，dist[] 中存储了从源点到其他所有节点的最短路径。

 

算法特点

贪心算法：Dijkstra算法是一种贪心算法，它总是选择当前未处理节点中距离源点最近的节点。
逐步构建：算法逐步构建最短路径树，最终形成从源点到所有其他节点的最短路径。
非负权重：Dijkstra算法仅适用于边权重非负的图。

算法限制

不支持负权重：如果图中存在负权重边，Dijkstra算法可能无法找到正确的最短路径。
效率问题：在稠密图中，算法的时间复杂度可能较高，因为它需要检查所有邻接节点。

时间复杂度

Dijkstra算法的时间复杂度通常为O(V^2)，其中V是图中节点的数量。使用优先队列（如二叉堆）可以优化到O((V+E)logV)，其中E是边的数量。

应用场景

Dijkstra算法广泛应用于需要找到最短路径的场合，如地图导航、网络路由、交通规划等。它的简单性和效率使其成为解决单源最短路径问题的首选算法之一。

3.算法代码展示

C++版本

#define _CRT_SECURE_NO_WARNINGS
#include <iostream>
#include <vector>
#include <climits>

using namespace std;

#define V 7  // 图中节点的数量
#define INF INT_MAX  // 无穷大

// 选择未处理的节点中距离最小的节点
int minDistance(vector<int>& dist, vector<int>& sptSet) {
    int min = INF, min_index;
    for (int v = 0; v < V; v++) {
        if (!sptSet[v] && dist[v] <= min) {
            min = dist[v];
            min_index = v;
        }
    }
    return min_index;
}

// Dijkstra算法
void dijkstra(vector<vector<int>>& graph, int start) {
    vector<int> dist(V, INF);  // 最短距离数组
    vector<int> sptSet(V, 0);  // 最短路径树集合（标记已处理的节点,未处理设置成0）

    dist[start] = 0;  // 源点的距离为0

    for (int count = 0; count < V - 1; count++) {
        int u = minDistance(dist, sptSet);  // 选择未处理节点中距离最小的节点
        sptSet[u] = 1;  // 标记为已处理

        // 更新相邻节点的最短距离
        for (int v = 0; v < V; v++) {
            if (!sptSet[v] && graph[u][v] != 0 && dist[u] != INF && dist[u] + graph[u][v] < dist[v]) {
                dist[v] = dist[u] + graph[u][v];
            }
        }
    }

    // 打印最短路径
    cout << "从节点 " << start << " 到各节点的最短路径：" << endl;
    for (int i = 0; i < V; i++) {
        cout << "到节点 " << i << ": " << dist[i] << endl;
    }
}

int main() {
    // 图的邻接矩阵表示，假设无向图
    /*vector<vector<int>> graph = {
        {0, 1, 4, 0},
        {1, 0, 2, 5},
        {4, 2, 0, 1},
        {0, 5, 1, 0}
    };*/
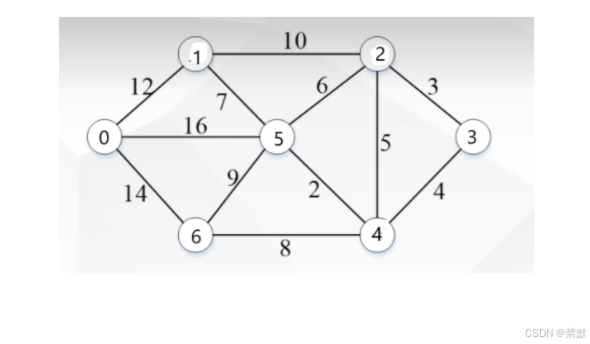
    vector<vector<int>> graph = {
        {0, 12, 0, 0, 0, 16,14},
        {12, 0, 10,0, 0, 7, 0},
        {0, 10, 0, 3, 5, 6, 0},
        {0,  0, 3, 0, 4, 0, 0},
        {0,  0, 5, 4, 0, 2, 8},
        {16, 7, 6, 0, 2, 0, 9},
        {14, 0, 0 ,0, 8, 9, 0},
    };
    dijkstra(graph, 3);  // 从节点0开始
    return 0;
}

C版本（与C++几乎没有区别）

#include <stdio.h>
#include <limits.h>

#define V 7  // 图中节点的数量
#define INF INT_MAX  // 无穷大

// 选择未处理的节点中距离最小的节点
int minDistance(int dist[], int sptSet[]) {
    int min = INF, min_index;
    for (int v = 0; v < V; v++) {
        if (!sptSet[v] && dist[v] <= min) {
            min = dist[v];
            min_index = v;
        }
    }
    return min_index;
}

// Dijkstra算法
void dijkstra(int graph[V][V], int start) {
    int dist[V];  // 最短距离数组
    int sptSet[V];  // 最短路径树集合（标记已处理的节点）

    // 初始化所有距离为无穷大，已处理节点标记为0
    for (int i = 0; i < V; i++) {
        dist[i] = INF;
        sptSet[i] = 0;
    }

    dist[start] = 0;  // 源点的距离为0

    for (int count = 0; count < V - 1; count++) {
        int u = minDistance(dist, sptSet);  // 选择未处理节点中距离最小的节点
        sptSet[u] = 1;  // 标记为已处理

        // 更新相邻节点的最短距离
        for (int v = 0; v < V; v++) {
            if (!sptSet[v] && graph[u][v] != 0 && dist[u] != INF && dist[u] + graph[u][v] < dist[v]) {
                dist[v] = dist[u] + graph[u][v];
            }
        }
    }

    // 打印最短路径
    printf("从节点 %d 到各节点的最短路径：\n", start);
    for (int i = 0; i < V; i++) {
        printf("到节点 %d: %d\n", i, dist[i]);
    }
}

int main() {
    // 图的邻接矩阵表示，假设无向图
    int graph[V][V] = {
        {0, 12, 0, 0, 0, 16,14},
        {12, 0, 10,0, 0, 7, 0},
        {0, 10, 0, 3, 5, 6, 0},
        {0,  0, 3, 0, 4, 0, 0},
        {0,  0, 5, 4, 0, 2, 8},
        {16, 7, 6, 0, 2, 0, 9},
        {14, 0, 0 ,0, 8, 9, 0},
    };

    dijkstra(graph, 3);  // 从节点0开始

    return 0;
}

若自己控制输入输出，在函数中增加一个参数就行，将节点数传入函数即可！