前言：在二叉搜索树（BST）中，查找、插入和删除操作的效率依赖于树的高度。如果树不平衡，它的性能可能会大大降低，接近 O(n)。为了解决这个问题，AVL 树也就应运而生。

在开始学习之前，先让我们看一下本文大致的讲解内容：

1.AVL树的概念

        在正式的学习Java中的AVL树之前，先让我们了解一下什么是AVL树：

        AVL 树是一种自平衡的二叉搜索树（BST），以其发明者 G. M. Adelson-Velsky 和 E. M. Landis 的名字命名。

        与普通的二叉搜索树不同，AVL 树在每次插入和删除节点后会自动进行调整，以保证树的平衡。

        AVL 树通过控制每个节点的左右子树高度差不超过 1 来保持平衡。这样的设计保证了在最坏情况下，AVL 树的高度为 O(log n)，从而提高了查找、插入和删除操作的效率。

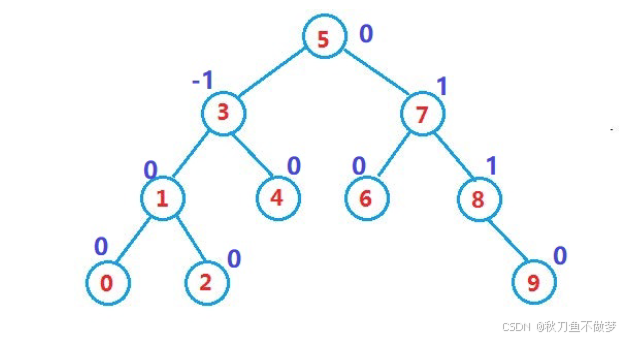
        就跟前言中提及的一样，AVL树的出现就是为了解决在二叉搜索树中，查找、插入和删除操作的性能降低问题，提高搜索效率。

        当然，看完上述有关AVL树的简介之后，我们还是不能很好的理解Java中的AVL树，接下来让我们一层一层的拨开其神秘的面纱。

 

2.AVL树节点的定义

        AVL树是一棵平衡二叉搜索树，既然是树，那么就会有节点的定义，而AVL树的节点的定义如下：

public static class AVLTreeNode {
    public int val;           // 节点的值
    public AVLTreeNode left;   // 左子节点
    public AVLTreeNode right;  // 右子节点
    public AVLTreeNode parent; // 父节点
    public int bf;             // 平衡因子 (Balance Factor)

    // 构造函数，用于创建带有指定值的节点
    public AVLTreeNode(int val) {
        this.val = val;        // 初始化节点的值
    }
}

这里我们在进行解释一下：

AVL 树节点类解释：

1. val：节点的值，表示存储在该节点中的整数。

2. left：左子节点，指向该节点的左孩子。如果没有左孩子，则为 null。

3. right：右子节点，指向该节点的右孩子。如果没有右孩子，则为 null。

4. parent：父节点，指向该节点的父节点。如果该节点是根节点，则 parent 为 null。

5. bf：平衡因子（Balance Factor），表示当前节点左右子树的高度差。平衡因子的值可以是 -1、0 或 1，用于决定是否需要旋转以保持 AVL 树的平衡性。

        这样我们就了解了Java中AVL树的节点的定义了！接下来让我们将一个一个的节点插入二叉树中创建一棵AVL树吧。

 

3.AVL树的插入操作

         AVL树就是在二叉搜索树的基础上引入了平衡因子，因此AVL树也可以看成是二叉搜索树。那么AVL树的插入过程可以分为两步：

1. 按照二叉搜索树的方式插入新节点

2. 调整节点的平衡因子

Java中AVL树的插入操作代码：

public void insertAVLTreeNode(int val) {
    // 插入节点
    AVLTreeNode node = new AVLTreeNode(val); // 创建一个新的 AVL 树节点
    if (root == null) { // 如果根节点为空，直接将新节点设为根节点
        root = node;
        return;
    }
    
    AVLTreeNode prev = null; // prev 用于保存当前遍历节点的父节点
    AVLTreeNode cur = root; // 从根节点开始查找插入位置
    
    // 寻找插入位置
    while (cur != null) {
        if (cur.val < val) { // 如果当前节点的值小于待插入值，移动到右子树
            prev = cur;
            cur = cur.right;
        } else if (cur.val > val) { // 如果当前节点的值大于待插入值，移动到左子树
            prev = cur;
            cur = cur.left;
        } else {
            // 如果当前节点的值等于待插入值，不做任何操作，直接返回（不允许重复节点）
            return;
        }
    }

    // 插入新节点
    if (prev.val < val) {
        prev.right = node; // 将新节点作为父节点的右子节点
    } else {
        prev.left = node;  // 将新节点作为父节点的左子节点
    }

    cur = node; // 当前节点指向新插入的节点
    AVLTreeNode parent = cur.parent; // 获取当前节点的父节点

    // 修改平衡因子 + 检查是否满足 AVL 树的平衡条件
    while (parent != null) { // 从新插入的节点向上更新平衡因子
        if (parent.left == node) {
            parent.bf--; // 如果新节点是左子树，平衡因子减 1
        } else {
            parent.bf++; // 如果新节点是右子树，平衡因子加 1
        }

        // 如果平衡因子为 0，子树高度没有变化，树保持平衡，直接返回
        if (parent.bf == 0) {
            return;
        } 
        // 如果平衡因子为 1 或 -1，树还是平衡的，继续向上更新
        else if (parent.bf == 1 || parent.bf == -1) {
            cur = parent;  // 向上移动
            parent = cur.parent; // 更新父节点
        } 
        // 如果平衡因子为 2 或 -2，表示需要进行旋转操作来保持平衡
        else {
            if (parent.bf == 2) { // 左子树高，需要左旋
                if (cur.bf == 1) {
                    rotateLeft(parent); // 单左旋
                } else {
                    rotateRL(parent); // 先右后左旋 (RL)
                }
            } else {
                // parent.bf == -2, 右子树高，需要右旋
                if (cur.bf == -1) {
                    rotateRight(parent); // 单右旋
                } else {
                    rotateLR(parent); // 先左后右旋 (LR)
                }
            }
        }
    }
}

上述代码的总梳理：

1. 节点插入：首先找到合适的位置，插入新节点到二叉搜索树的正确位置。

2. 更新平衡因子：在插入新节点后，需要从插入节点开始逐层向上更新其祖先节点的平衡因子（bf）。

3. 检查是否需要旋转

   ：如果某个祖先节点的平衡因子绝对值大于 1，就需要通过旋转操作恢复平衡。

   • 左旋（rotateLeft）：当插入导致某个节点的左子树过高时。

   • 右旋（rotateRight）：当插入导致某个节点的右子树过高时。

   • 左右旋（rotateRL）：当插入到右子树的左子树时，需要先右旋再左旋。

   • 右左旋（rotateLR）：当插入到左子树的右子树时，需要先左旋再右旋。

        当然，读者读到此处会问，什么是左旋，什么又是右旋，左右旋又是什么东西？这些东西又是干什么用的呢？接着往下看即可。

 

4.AVL树旋转操作

        在AVL树的创建中，旋转使AVL树平衡是必不可少的，如果在一棵原本是平衡的AVL树中插入一个新节点，就可能造成不平衡，此时必须调整树的结构，使之平衡化。

        根据节点插入位置的不同，AVL树的旋转分为四种：

        （1）新节点插入较高右子树的右侧---左单旋

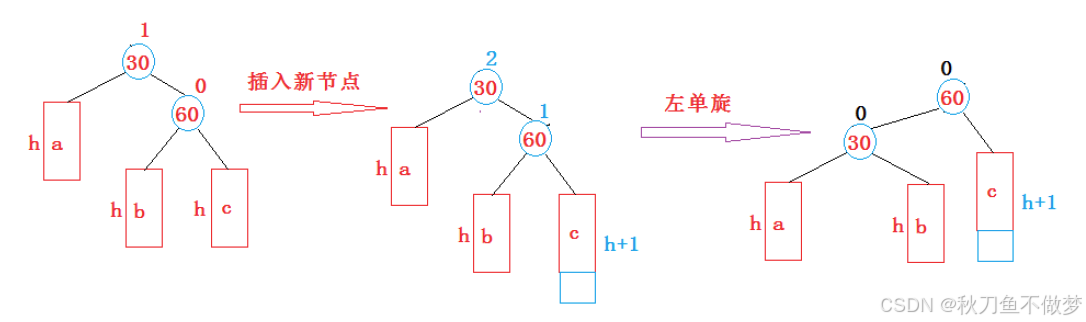
以下为Java中实现AVL树左单旋的代码：

public void rotateLeft(AVLTreeNode parent) {
    // 获取当前失衡节点的右子节点
    AVLTreeNode subR = parent.right; 
    // 获取右子节点的左子节点，因为旋转后这个节点将成为父节点的右子节点
    AVLTreeNode subRL = subR.left;

    // 执行左旋：将 parent 的右子节点指向 subR 的左子节点
    parent.right = subRL;
    // 将 subR 的左子节点指向 parent
    subR.left = parent;

    // 如果 subR 的左子节点存在，更新其父节点为 parent
    if (subRL != null) {
        subRL.parent = parent;
    }

    // 获取 parent 的父节点，以便更新连接
    AVLTreeNode parParent = parent.parent;
    // 将 parent 的父节点指向 subR
    parent.parent = subR;

    // 如果 parent 是根节点，更新根节点为 subR
    if (parent == root) {
        root = subR;
        subR.parent = null; // 新根节点的父节点应为空
    } else {
        // 如果 parent 不是根节点，根据 parent 是其父节点的左子节点还是右子节点，更新父节点的指针
        if (parParent.left == parent) {
            parParent.left = subR; // 如果 parent 是左子节点，更新为 subR
        } else {
            parParent.right = subR; // 如果 parent 是右子节点，更新为 subR
        }
        subR.parent = parParent; // 更新 subR 的父节点为 parent 的父节点
    }

    // 更新平衡因子，旋转后 parent 和 subR 的平衡因子都恢复为 0
    parent.bf = subR.bf = 0;
}

代码解释：

1. 获取右子节点：subR = parent.right 表示我们要对 parent 节点进行左旋操作，旋转的是 parent 的右子节点。
2. 重新连接节点：在左旋操作中，parent 的右子节点（subR）上升，成为新的父节点，原来的 parent 降为 subR 的左子节点。
3. 处理子树：如果 subR 的左子节点存在，左旋后需要将这个左子节点接到 parent 的右子树上。
4. 根节点的特殊处理：如果 parent 是根节点，则旋转后 subR 成为新的根节点，否则，更新 parent 的父节点（parParent）的子节点指向。
5. 更新平衡因子：由于旋转操作恢复了子树的平衡，parent 和 subR 的平衡因子都设置为 0。

 

        （2）新节点插入较高左子树的左侧---右单旋

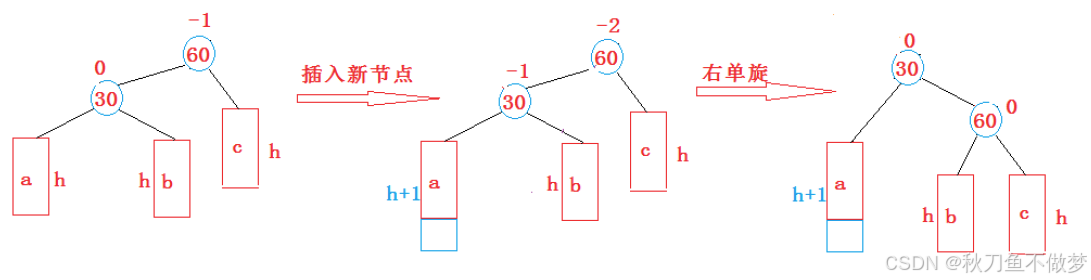
以下为Java中实现AVL树左单旋的代码：    

public void rotateRight(AVLTreeNode parent) {
    // 获取parent的左子节点
    AVLTreeNode subL = parent.left;
    // 获取subL的右子节点，用于更新parent的左子节点
    AVLTreeNode subLR = subL.right;

    // 将parent的左子节点更新为subL的右子节点
    parent.left = subLR;
    // 将subL的右子节点设为parent，完成右旋
    subL.right = parent;

    // 如果subLR不为空，将其父节点设为parent
    if (subLR != null) {
        subLR.parent = parent;
    }

    // 获取parent的父节点parParent
    AVLTreeNode parParent = parent.parent;
    // 更新parent的父节点为subL
    parent.parent = subL;

    // 如果parent是根节点，更新根节点为subL
    if (parent == root) {
        root = subL;
        subL.parent = null;  // subL成为新的根节点，没有父节点
    } else {
        // 否则，判断parent是parParent的左子节点还是右子节点
        if (parParent.left == parent) {
            parParent.left = subL;  // 如果parent是左子节点，更新parParent的左子节点为subL
        } else {
            parParent.right = subL; // 如果parent是右子节点，更新parParent的右子节点为subL
        }
        // 更新subL的父节点为parParent
        subL.parent = parParent;
    }

    // 更新平衡因子，旋转后平衡因子都归为0
    subL.bf = parent.bf = 0;
}

代码解释：

1. subL、subLR的获取：首先获取 parent 节点的左子节点 subL，并从 subL 获取其右子节点 subLR。这些节点用于旋转过程中重新构建子树。
2. 子节点指针的更新：在旋转时，parent 的左子节点被更新为 subL 的右子节点，而 subL 的右子节点被更新为 parent。
3. 父节点更新：在旋转过程中，必须更新 parent 和 subL 的父节点关系。如果 parent 是根节点，旋转后的根节点需要更新为 subL。

 

        （3）新节点插入较高左子树的右侧：先左单旋再右单旋（左右双旋）

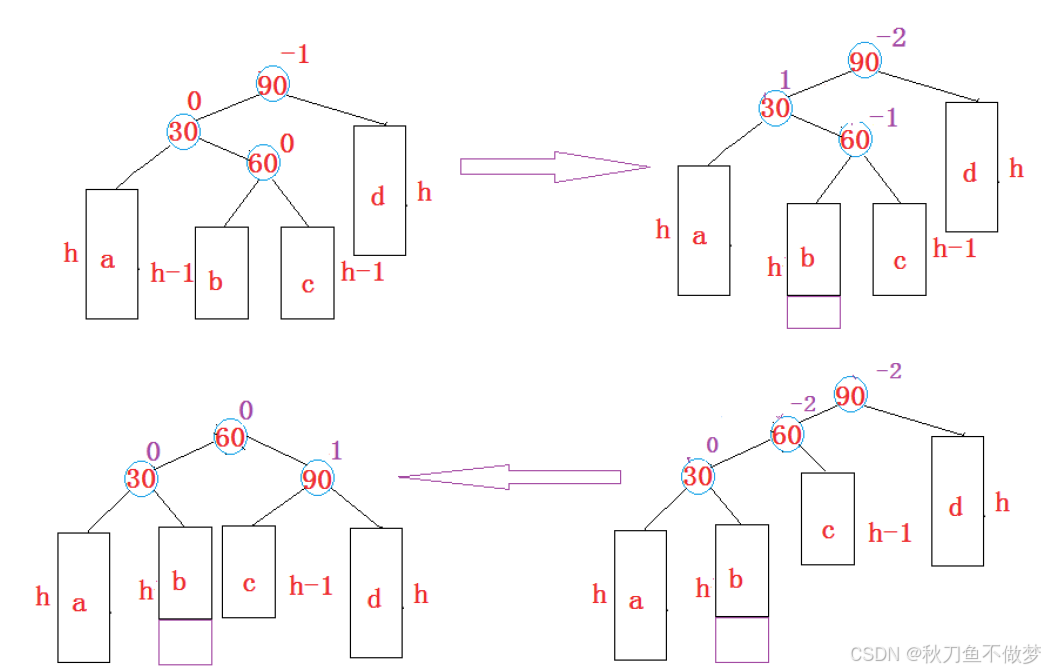
以下为Java中实现AVL树左右双旋的代码： 

public void rotateLR(AVLTreeNode parent) {
    // 获取parent的左子节点
    AVLTreeNode subL = parent.left;
    // 获取subL的右子节点
    AVLTreeNode subLR = subL.right;
    // 记录subLR的平衡因子
    int valBF = subLR.bf;

    // 先对subL进行左旋转
    rotateLeft(subL);
    // 然后对parent进行右旋转
    rotateRight(parent);

    // 根据subLR的平衡因子更新旋转后的节点平衡因子
    if (valBF == -1) {
        // 如果subLR的平衡因子为-1，更新parent的平衡因子为1，subLR和subL的平衡因子为0
        parent.bf = 1;
        subLR.bf = 0;
        subL.bf = 0;
    } else if (valBF == 1) {
        // 如果subLR的平衡因子为1，更新subL的平衡因子为-1，parent的平衡因子为0，subLR的平衡因子为0
        subL.bf = -1;
        parent.bf = 0;
        subLR.bf = 0;
    }
}

代码解释：

1. 获取子节点：首先获取 parent 的左子节点 subL 和 subL 的右子节点 subLR，并记录 subLR 的平衡因子。
2. 旋转操作：先对 subL 进行左旋转，然后对 parent 进行右旋转。这两次旋转是处理左-右情况（LR）的标准操作。
3. 更新平衡因子：根据 subLR 的原始平衡因子（valBF），更新旋转后节点的平衡因子。subLR 的平衡因子决定了旋转后的树的平衡状态。

 

        （4）新节点插入较高右子树的左侧---右左：先右单旋再左单旋（右左双旋）

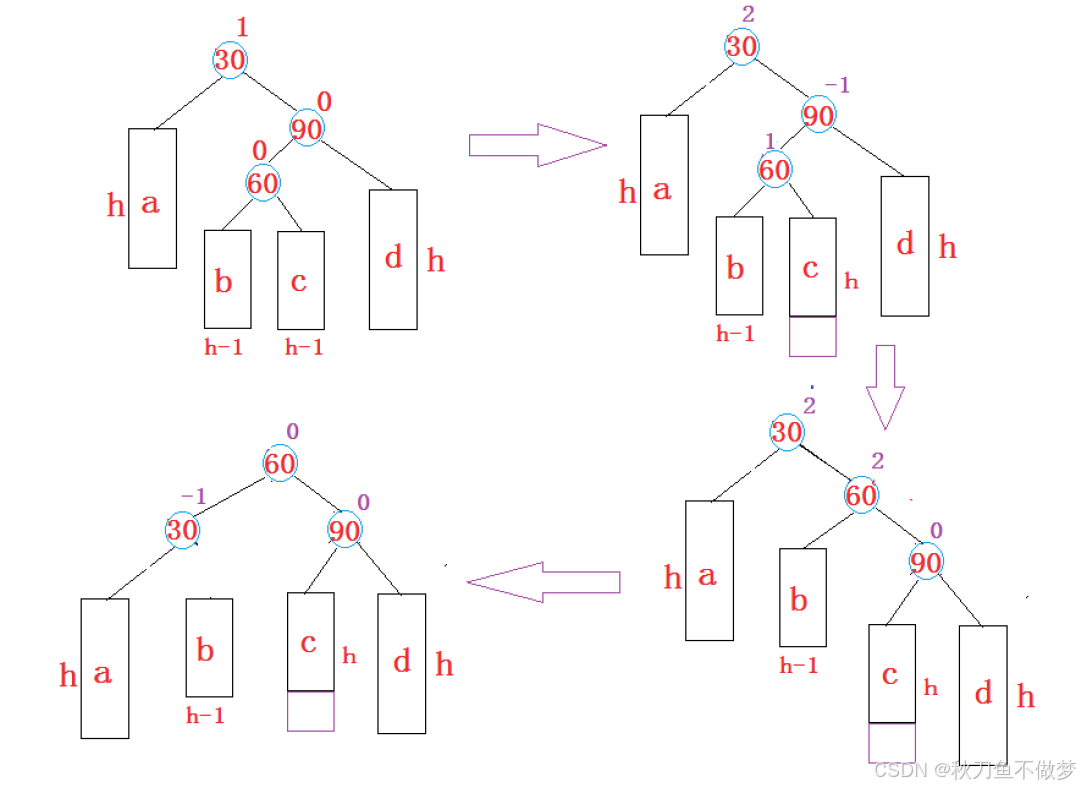
以下为Java中实现AVL树右左双旋的代码： 

public void rotateRL(AVLTreeNode parent) {
    // 获取parent的右子节点
    AVLTreeNode subR = parent.right;
    // 获取subR的左子节点
    AVLTreeNode subRL = subR.left;
    // 记录subRL的平衡因子
    int valBF = subRL.bf;

    // 先对subR进行右旋转
    rotateRight(subR);
    // 然后对parent进行左旋转
    rotateLeft(parent);

    // 根据subRL的平衡因子更新旋转后的节点平衡因子
    if (valBF == -1) {
        // 如果subRL的平衡因子为-1，更新parent的平衡因子为0，subRL的平衡因子为0，subR的平衡因子为1
        parent.bf = 0;
        subRL.bf = 0;
        subR.bf = 1;
    } else if (valBF == 1) {
        // 如果subRL的平衡因子为1，更新parent的平衡因子为-1，subRL的平衡因子为0，subR的平衡因子为0
        parent.bf = -1;
        subRL.bf = 0;
        subR.bf = 0;
    }
}

代码解释：

1. 获取子节点：首先获取 parent 的右子节点 subR 和 subR 的左子节点 subRL，并记录 subRL 的平衡因子。
2. 旋转操作：先对 subR 进行右旋转，然后对 parent 进行左旋转。这两个旋转操作用于处理右-左情况（RL）。
3. 更新平衡因子：根据 subRL 的原始平衡因子（valBF），更新旋转后节点的平衡因子。subRL 的平衡因子决定了旋转后树的平衡状态。

        通过以上的讲解，读者应该大致的了解了Java中AVL树的旋转操作了，也正是通过上述的旋转操作，解决了普通的二叉搜索树的单枝问题（时间复杂度O(N)）。

 

5.AVL树的验证

        AVL树是在二叉搜索树的基础上加入了平衡性的限制，因此要验证AVL树，可以分两步：

1. 验证其为二叉搜索树 如果中序遍历可得到一个有序的序列，就说明为二叉搜索树

2. 验证其为平衡树 每个节点子树高度差的绝对值不超过1(注意节点中如果没有平衡因子) 节点的平衡因子是否计算正确

那么我们就根据上述的原理，来对AVL树进行验证：

// 中序遍历树，按顺序打印节点值
public void inorder(TreeNode root) {
    if (root == null) {
        return; // 如果当前节点为空，直接返回
    }
    inorder(root.left); // 递归遍历左子树
    System.out.println(root.val); // 打印当前节点的值
    inorder(root.right); // 递归遍历右子树
}

// 判断一棵树是否为 AVL 树
public boolean isAVLTree(TreeNode root) {
    if (root == null) {
        return true; // 空树被认为是 AVL 树
    }

    // 获取当前节点的左子树和右子树的高度
    int left = getHeight(root.left);
    int right = getHeight(root.right);

    // 检查当前节点的平衡因子是否与计算的高度差一致
    if (right - left != root.bf) {
        return false; // 平衡因子计算错误，不是 AVL 树
    }

    // 递归检查左子树和右子树是否都是 AVL 树，并且当前节点的左右子树高度差不超过 1
    return Math.abs(right - left) <= 1 && isAVLTree(root.left)
            && isAVLTree(root.right);
}

// 获取树的高度
private int getHeight(TreeNode root) {
    if (root == null) {
        return 0; // 空节点高度为 0
    }
    if (root.left == null && root.right == null) {
        return 1; // 叶节点高度为 1
    }
    // 递归计算左子树和右子树的高度，取较大值并加 1
    return Math.max(getHeight(root.left), getHeight(root.right)) + 1;
}

解释：

1. inorder 方法：

   • 功能：中序遍历一棵树并打印每个节点的值。中序遍历的顺序是先左子树、再当前节点、最后右子树。
   • 实现：递归遍历左子树，打印当前节点的值，然后递归遍历右子树。

2. isAVLTree 方法：

   • 功能：判断给定的树是否为 AVL 树。
   • 实现：
     • 先计算当前节点的左右子树高度。
     • 检查节点的平衡因子是否与计算的高度差一致。
     • 递归检查左右子树是否都是 AVL 树，并确保左右子树高度差不超过 1。

3. getHeight 方法：

   • 功能：计算树的高度。
   • 实现：
     • 对于空节点，返回高度 0。
     • 对于叶节点（没有子节点），返回高度 1。
     • 对于其他节点，递归计算左右子树的高度，返回较大值加 1。

        通过上述的代码的返回值，我们就可以判断一棵树是否为AVL树了！

 

6.AVL树的删除操作

        对于Java中AVL树的删除操作，因为AVL树也是二叉搜索树，可按照二叉搜索树的方式将节点删除，然后再更新平衡因子，只不过与删除不同的是，删除节点后的平衡因子更新，最差情况下一直要调整到根节点的位置。

        其删除的基本思路为：

1、找到需要删除的节点
2、按照搜索树的删除规则删除节点
3、更新平衡因子，如果出现了不平衡，进行旋转。--单旋，双旋

        由于AVL书的删除操作过于庞大与复杂，这里我们不做过多的解释，如果读者有兴趣，可以上网查阅资料或者可以参考《算法导论》这本书中的推演。

 

7.AVL树性能分析

        AVL树是一棵绝对平衡的二叉搜索树，其要求每个节点的左右子树高度差的绝对值都不超过1，这样可以保证查询时高效的时间复杂度。

        但是如果要对AVL树做一些结构修改的操作，性能非常低下，比如：插入时要维护其绝对平衡，旋转的次数比较多，更差的是在删除时，有可能一直要让旋转持续到根的位置。

        因此如果需要一种查询高效且有序的数据结构，而且数据的个数为静态的(即不会改变)，可以考虑AVL树，但一个结构经常修改，就不太适合。