前言：Java 提供了丰富的数据结构来处理和管理数据，其中 TreeSet 和 TreeMap 是基于红黑树实现的集合和映射接口。它们有序地存储数据，提供高效的搜索、插入和删除操作。

先让我们看一下本文大致的讲解内容

1.二叉搜索树的认识

        （1）二叉搜索树的概念

        在开始学习TreeSet与TreeMap之前，我们需要先学习一下Java中的二叉搜索树，二叉搜索树是一种特殊的二叉树，其中每个节点都有一个值，并满足以下性质：

• 对于每个节点，左子树所有节点的值都小于该节点的值。

• 对于每个节点，右子树所有节点的值都大于该节点的值。

如图：

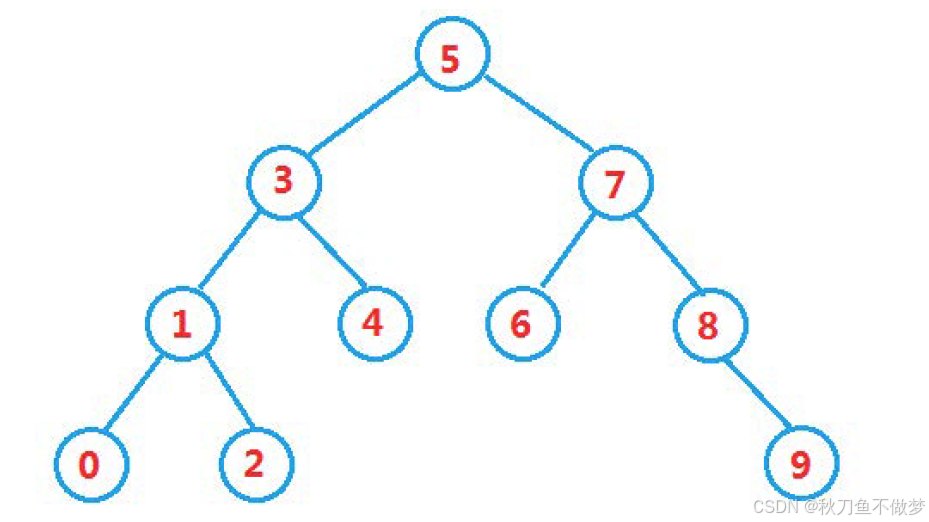
从上图中我们可以很明显的观察出二叉搜索树的上述两个特性。

 

        （2）二叉搜索树的性质

        在了解完了二叉搜索树的概念之后，我们需要学习一下有关二叉搜索树的性质，对于一棵二叉搜索树而言，其都有以下三个性质：

• 有序性：二叉搜索树的中序遍历结果是一个递增的有序序列。

• 动态性：二叉搜索树支持动态插入和删除操作，适用于需要频繁更新的数据集合。

• 查找效率：在理想情况下，二叉搜索树的查找、插入和删除操作的时间复杂度为 O(log n)。

        ——这里读者可能会对其中的一些性质不是很理解，没有关系，继续向下进行阅读即可，在后续的文本中，我们会慢慢的理解其中的意思。

 

2.有关二叉搜索树的常用操作

        【1】插入操作

        插入操作用于向二叉搜索树中插入新值。插入过程从根节点开始，根据当前节点的值与新值的比较结果，决定将新值插入到左子树还是右子树。

以下是实现该操作的代码：

public void insertNode(int key) {
    // 如果根节点为空，直接插入新节点作为根节点
    if (root == null) {
        root = new TreeNode(key);
        return;
    }

    // 初始化当前节点为根节点，父节点为null
    TreeNode cur = root;
    TreeNode parent = null;
    TreeNode node = new TreeNode(key);

    // 寻找合适的位置插入节点
    while (cur != null) {
        if (cur.val < key) { // 当前值小于插入值，向右子树移动
            parent = cur;
            cur = cur.right;
        } else if (cur.val > key) { // 当前值大于插入值，向左子树移动
            parent = cur;
            cur = cur.left;
        } else { // 当前值等于插入值，直接返回，不插入重复值
            return;
        }
    }

    // 根据父节点值与插入值的比较结果，插入新节点到左子树或右子树
    if (parent.val > key) {
        parent.left = node;
    } else {
        parent.right = node;
    }
}

 

读者可以跟着下面的解释来对上边的代码进行理解：

1. 根节点为空检查：

   • 如果 root 为空，直接将新节点 TreeNode(key) 作为根节点插入，并返回。

2. 初始化当前节点和父节点：

   • cur 用于遍历树，从 root 开始。
   • parent 用于记录 cur 的父节点。

3. 寻找合适的插入位置：

   • 当 cur 不为空时，比较 cur.val 与 key：
     • 如果 cur.val 小于 key，移动到右子树。
     • 如果 cur.val 大于 key，移动到左子树。
     • 如果 cur.val 等于 key，直接返回，不插入重复值。

4. 插入新节点：

   • 根据 parent.val 与 key 的比较结果，将新节点插入到 parent 的左子树或右子树。

        ——这样我们就学会了插入操作了！

 

        【2】查找操作

        查找操作用于在二叉搜索树中查找特定值。查找过程从根节点开始，根据当前节点的值与目标值的比较结果，决定在左子树还是右子树继续查找。

以下是实现该操作的代码：

public TreeNode search(int key) {
    // 初始化当前节点为根节点
    TreeNode cur = root;
    
    // 遍历树，直到找到目标节点或遍历到空节点
    while (cur != null) {
        if (cur.val < key) { // 当前节点值小于目标值，移动到右子树
            cur = cur.right;
        } else if (cur.val > key) { // 当前节点值大于目标值，移动到左子树
            cur = cur.left;  // 这里应修正为cur = cur.left;
        } else { // 找到目标节点
            return cur;
        }
    }
    // 如果没有找到目标节点，返回 null
    return null;
}

读者可以跟着下面的解释来对上边的代码进行理解：

1. 初始化当前节点：

   • cur 用于遍历树，从 root 开始。

2. 遍历树：

   • 当 cur 不为空时，比较 cur.val 与 key：
     • 如果 cur.val 小于 key，移动到右子树 (cur = cur.right)。
     • 如果 cur.val 大于 key，移动到左子树 (cur = cur.left)。
     • 如果 cur.val 等于 key，返回当前节点。

3. 返回结果：

   • 如果遍历完整棵树没有找到目标节点，返回 null。

 

        【3】删除操作

        删除操作用于从二叉搜索树中删除指定值。删除节点分为三种情况：叶子节点、只有一个子节点的节点和有两个子节点的节点。

        由于删除操作比较哦啊复杂，所以我们这里重点讲解一下，对于删除操作，我们可能会有以下的可能情况：

——现在我们假设待删除结点为 cur, 待删除结点的双亲结点为 parent：

1.cur.left == null

        1. cur 是 root，则 root = cur.right
        2. cur 不是 root，cur 是 parent.left，则 parent.left = cur.right
        3. cur 不是 root，cur 是 parent.right，则 parent.right = cur.right

2.cur.right == null

        1. cur 是 root，则 root = cur.left
        2. cur 不是 root，cur 是 parent.left，则 parent.left = cur.left

        3. cur 不是 root，cur 是 parent.right，则 parent.right = cur.left

3.cur.left != null && cur.right != null

        这时我们就需要使用替换法进行删除，即在它的右子树中寻找中序下的第一个结点(关键码最小)，用它的值填补到被删除节点中，再来处理该结点的删除问题

我们大致了解了删除的三种可能的大情况之后，现在让我们尝试着编写一下代码：

public void remove(int key) {
    TreeNode parent = null; // 父节点初始化为 null
    TreeNode cur = root; // 当前节点初始化为根节点
    // 遍历树，寻找要删除的节点
    while (cur != null) {
        if (cur.val < key) { // 当前值小于目标值，移动到右子树
            parent = cur;
            cur = cur.right;
        } else if (cur.val > key) { // 当前值大于目标值，移动到左子树
            parent = cur;
            cur = cur.left;
        } else { // 找到目标节点
            removeNode(parent, cur); // 调用辅助方法删除节点
            return; // 删除节点后退出方法
        }
    }
}

private void removeNode(TreeNode parent, TreeNode cur) {
    if (cur.right == null) { // 当前节点没有右子树
        if (cur == root) { // 当前节点是根节点
            root = root.left; // 根节点指向左子树
        } else if (parent.left == cur) { // 当前节点是父节点的左子节点
            parent.left = cur.left; // 父节点左子节点指向当前节点的左子树
        } else { // 当前节点是父节点的右子节点
            parent.right = cur.left; // 父节点右子节点指向当前节点的左子树
        }
    } else if (cur.left == null) { // 当前节点没有左子树
        if (cur == root) { // 当前节点是根节点
            root = root.right; // 根节点指向右子树
        } else if (parent.left == cur) { // 当前节点是父节点的左子节点
            parent.left = cur.right; // 父节点左子节点指向当前节点的右子树
        } else { // 当前节点是父节点的右子节点
            parent.right = cur.right; // 父节点右子节点指向当前节点的右子树
        }
    } else { // 当前节点有两个子节点
        TreeNode targetParent = cur; // 目标节点的父节点初始化为当前节点
        TreeNode target = cur.right; // 目标节点初始化为当前节点的右子节点
        // 寻找右子树中的最左节点
        while (target.left != null) {
            targetParent = target;
            target = target.left;
        }
        cur.val = target.val; // 用右子树中最左节点的值替换当前节点的值
        // 调整指针以删除目标节点
        if (targetParent.left == target) {
            targetParent.left = target.right;
        } else {
            targetParent.right = target.right;
        }
    }
}

——这里我们给每一条代码都加上了注释，读者可以根据注释来对上述代码进行理解！！！

这样我们就了解了二叉搜索树中常用的操作了.

 

3.二叉树的应用场景

        学习完二叉树的概念以及其基本的使用之后，让我们来学习一些二叉树的应用场景，二叉树（Binary Tree）在日常中有着广泛的应用。以下是一些主要的实际应用场景：

1. 数据结构和算法

• 二叉搜索树（BST）：用于实现高效的搜索、插入和删除操作，时间复杂度平均为 O(log n)。

• 平衡树（如AVL树、红黑树）：这些是自平衡二叉搜索树，确保树的高度保持在 O(log n)，从而提供高效的操作。

• 堆（Heap）：二叉堆用于实现优先队列。最大堆用于实现高效的最大值查找，最小堆用于最小值查找。

2. 数据库和文件系统

• B树和B+树：这些是多路搜索树，常用于数据库索引和文件系统索引，以提高查询和检索的效率。

• Trie树：一种多叉树，用于实现前缀匹配，常用于字典存储和自动补全功能。

3. 图形和游戏开发

• 四叉树和八叉树：用于空间分割，以提高碰撞检测、渲染和其他空间查询操作的效率。

• 场景图（Scene Graph）：在3D图形引擎中，场景图是一个树状结构，用于管理和渲染场景中的对象。

这样我们就大致的了解了二叉树在今后的日常中有哪些用武之地了！！！