1.如何衡量算法好坏
小编认为衡量算法的好坏，主要是看算法的效率之时间复杂度和空间复杂度。
2.算法效率
算法效率分析分为两种：第一种是时间效率，第二种是空间效率 。 时间效率被称为时间复杂度 而空间效率被称作 空间复杂度 。 时间复杂度主要衡量的是一个算法的运行速度，而空间复杂度主要衡量一个算法所需要的额外空间。
3.时间复杂度
3.1.时间复杂度概念
时间复杂度的定义：在计算机科学中， 算法的时间复杂度是一个数学函数，它定量描述了该算法的运行时间。一个 算法执行所耗费的时间，从理论上说，是不能算出来的，只有你把你的程序放在机器上跑起来，才能知道。算法中的基本操作的执行次数，为算法的时间复杂度。
3.2.大O渐进的表示法
如下代码：
int N=9;
int count = 0;
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
count++;
}
}
for (int k = 0; k < 2 * N ; k++) {
count++;
}
int M = 10;
while ((M--) > 0) {
count++;
}
System.out.println(count);
}代码执行次数是（N^2+2*N+10）
实际中我们计算时间复杂度时，我们其实并不一定要计算精确的执行次数，而只需要 大概执行次
数，那么这里我们 使用大 O 的渐进表示法。
3.3.大O渐进法的计算
1、用常数1取代运行时间中的所有加法常数。2、在修改后的运行次数函数中，只保留最高阶项。3、如果最高阶项存在且不是1，则去除与这个项目相乘的常数。得到的结果就是大O阶。
那么用大O渐进法表示上述代码的时间复杂度是O（ N^2）
通过上面举例我们发现大O渐进法帮我们去掉了对我们影响不大的项，简化了时间复杂度的表达方式。
另外有些算法的时间复杂度存在最好、平均和最坏情况：最坏情况：任意输入规模的最大运行次数 ( 上界 )平均情况：任意输入规模的期望运行次数最好情况：任意输入规模的最小运行次数 ( 下界 )
但是一般以最坏的情况来表示。
3.4.常见的时间复杂度
代码一：
void func2(int N) {
int count = 0;
for (int k = 0; k < 2 * N ; k++) {
count++;
}
int M = 10;
while ((M--) > 0) {
count++;
}
System.out.println(count);
}此时就是：2*N+10；那么按照大O渐进法来算，去掉底次项，以及高次项的常数，其时间复杂度是O（N）。
代码二：
void func3(int N, int M) {
int count = 0;
for (int k = 0; k < M; k++) {
count++;
}
for (int k = 0; k < N ; k++) {
count++;
}
System.out.println(count);
}此时就是：M+N；那么大O渐进法，保留两个高次项后为：O（M+N）;
代码三：
void func4(int N) {
int count = 0;
for (int k = 0; k < 100; k++) {
count++;
}
System.out.println(count);
}此时就是：100；那么按照大O渐进法来说，将常数变为1，保留高次项后且其常数项变为1，所以这段代码的时间复杂度就是O（1）；
代码四：
void bubbleSort(int[] array) {
for (int end = array.length; end > 0; end--) {
boolean sorted = true;
for (int i = 1; i < end; i++) {
if (array[i - 1] > array[i]) {
Swap(array, i - 1, i);
sorted = false;
}
}
if (sorted == true) {
break;
}
}
}
此时就是:因为每次内部循环的条件都要减去1，所以就有一下表达式；
N+(N-1)+(N-2)+(N-3)+............(N-(N-1))+(N-N)，求和后：N^2/2;所以根据大O渐进法，这段代码的时间复杂度是O（N^2）；
代码五：
int binarySearch(int[] array, int value) {
int begin = 0;
int end = array.length - 1;
while (begin <= end) {
int mid = begin + ((end-begin) / 2);
if (array[mid] < value)
begin = mid + 1;
else if (array[mid] > value)
end = mid - 1;
else
return mid;
}
return -1;
}
如图所示：代码的执行次数如上，通过过折纸查找的方式：
所以时间复杂度为：O（x）.
代码六：
long factorial(int N) {
return N < 2 ? N : factorial(N-1) * N;
}此段代码，分析发现基本操作递归了N次，时间复杂度为O(N)。
代码七：
int fibonacci(int N) {
return N < 2 ? N : fibonacci(N-1)+fibonacci(N-2);
}
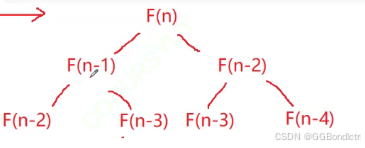
如上图：分别执行1次，2次，4次，.........,2^N;所以等比数列求和：为2^N-1;所以根据大O渐进法，保留高次项后，此段代码的时间复杂度为O（2^N）；
4.空间复杂度
空间复杂度是对一个算法在运行过程中 临时占用存储空间大小的量度 。空间复杂度不是程序占用了多少 bytes 的空 间，因为这个也没太大意义，所以空间复杂度算的是变量的个数。空间复杂度计算规则基本跟时间复杂度类似，也 使用大 O 渐进表示法 。
代码一：
void bubbleSort(int[] array) {
for (int end = array.length; end > 0; end--) {
boolean sorted = true;
for (int i = 1; i < end; i++) {
if (array[i - 1] > array[i]) {
Swap(array, i - 1, i);
sorted = false;
}
}
if (sorted == true) {
break;
}使用了常数个额外空间,所以空间复杂度为O（1）；
代码二：
int[] fibonacci(int n) {
long[] fibArray = new long[n + 1];
fibArray[0] = 0;
fibArray[1] = 1;
for (int i = 2; i <= n ; i++) {
fibArray[i] = fibArray[i - 1] + fibArray [i - 2];
}
return fibArray;动态开辟了N个空间，所以空间复杂度为O（N）；
