聚类是一种机器学习技术，它涉及到数据点的分组。给定一组数据点，我们可以使用聚类算法将每个数据点划分为一个特定的组。理论上，同一组中的数据点应该具有相似的属性或特征，而不同组中的数据点应该具有高度不同的属性或特征。

聚类算法在很多场景下都有应用，例如新闻自动分组，用户分群，图像分割等等。很多时候，无监督的聚类算法，得到的聚类结果还可以作为特征在后续监督学习中应用，提升整体效果。本文将介绍2种常用的聚类算法K-means与DBSCAN。

K-means算法

K-means是最经典的聚类算法之一。由于该算法的效率高，所以在对大规模数据进行聚类时被广泛应用。目前，许多算法均围绕着该算法进行扩展和改进。

K-means算法处理过程如下：

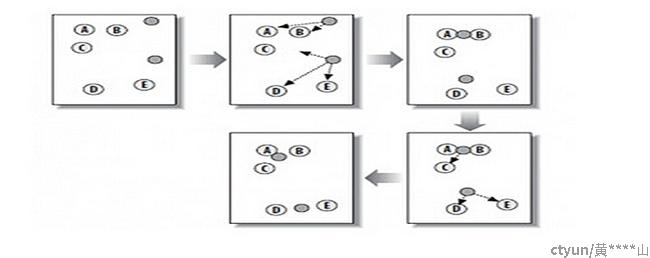
1. 确定聚类类别数k，在样本集中随机地选择k个样本，每个样本初始地代表了一个簇的平均值或质心；
2. 对剩余的每个样本，根据其与各簇中心的距离，将它划分到距离最短的簇，当所有样本都划分以后，就形成了K个数据集（即K个簇）；
3. 重新计算每个簇的数据对象的均值，将均值作为新的聚类中心；
4. 通过质心位置是否发生变化判断模型是否收敛，若收敛，则迭代结束，聚类完成；若不收敛，则进入步骤2，继续迭代，直到模型收敛；

K-means算法具有以下优点：

• 解决聚类问题的经典算法，简单、快速
• 当处理大数据集时，该算法保持可伸缩性和高效率
• 当簇为高斯分布时，它的效果较好

K-means算法具有以下缺点：

• 在簇的平均值可被定义的情况下才能使用，可能不适用于某些应用；
• 必须给出k的数值（要生成簇的数目），而且对初值敏感，即对于不同的初值，可能会导致不同结果；
• 不适合非凸形状的簇或者大小差别很大的簇；
• 对噪声和孤立点敏感；

DBSCAN算法

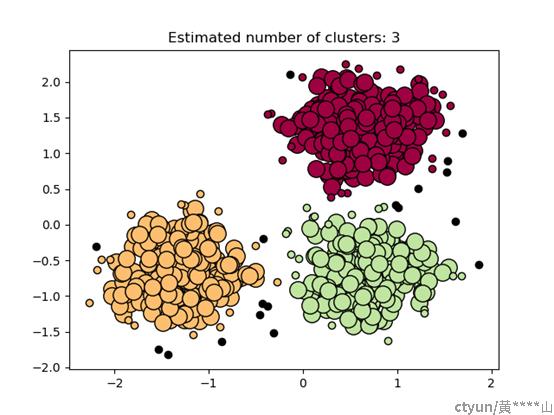
DBSCAN是一种非常著名的基于密度的聚类算法。其英文全称是 Density-Based Spatial Clustering of Applications with Noise，意思就是：一种基于密度，对噪声鲁棒的空间聚类算法。直观效果上看，DBSCAN算法可以找到样本点的全部密集区域，并把这些密集区域当做一个一个的聚类簇。

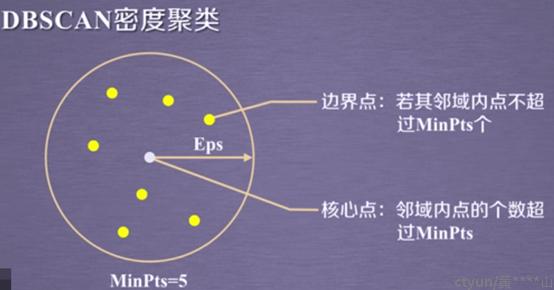
基本概念：

1. ϵ -邻域：对于xj∈D，其ϵ-邻域包含样本集D中与xj的距离不大于ϵ的子样本集，即Nϵ(xj)={xi∈D|distance(xi,xj)≤ϵ}, 这个子样本集的个数记为|Nϵ(xj)|。　
2. 核心对象：对于任一样本xj∈D，如果其ϵ-邻域对应的Nϵ(xj)至少包含MinPts个样本，即如果|Nϵ(xj)|≥MinPts，则xj是核心对象。
3. 密度直达：如果xi位于xj的ϵ-邻域中，且xj是核心对象，则称xi由xj密度直达。注意反之不一定成立，即此时不能说xj由xi密度直达, 除非xi也是核心对象。
4. 密度可达：对于xi和xj,如果存在样本序列p1,p2,...,pT,满足p1=xi,pT=xj, 且pt+1由pt密度直达，则称xj由xi密度可达。也就是说，密度可达满足传递性。此时序列中的传递样本p1,p2,...,pT−1均为核心对象，因为只有核心对象才能使其他样本密度直达。注意密度可达也不满足对称性，这个可以由密度直达的不对称性得出。
5. 密度相连：对于xi和xj,如果存在核心对象样本xk，使xi和xj均由xk密度可达，则称xi和xj密度相连。注意密度相连关系是满足对称性的。

有了以上基本概念，算法实现步骤就很简单了，主要分为3步：

1. 确定参数领域半径Eps及核心点领域最小样本数MinPts；
2. 从数据集中任意选取一个数据点p；
3. 如果对于参数Eps和MinPts，所选取的数据点p为核心点，则找出所有从p密度可达的数据点，形成一个簇。若选取的数据对象点p是边界点，则回到步骤2重新选取另一个数据点，重复上述过程直到数据选取完成。

算法优点：

• 可以对任意形状的稠密数据集进行聚类
• 可以在聚类的同时发现异常点，对数据集中的异常点不敏感
• 可以根据数据特点自行决定聚类类别数

算法缺点：

• 如果样本集的密度不均匀、聚类间距差相差很大时，聚类质量较差
• 如果样本集较大时，聚类收敛时间较长
• 调参相对于传统的K-Means之类的聚类算法稍复杂