1 神经网络的主要思想

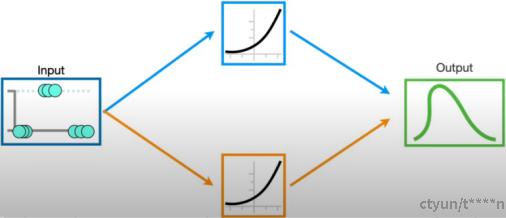
图. 模型训练基本结构

       如图1所示，我们对输入点集合数据，去制作一个曲线函数，使得这个曲线能尽量的覆盖所有的输入点。曲线函数由中间两个已经确定基本函数单元构成。最终通过训练，让中间的函数单元涉及到的参数最优，用于拟合逼近真实的所有的数据。其中两个中间函数曲线是通用的训练曲线(激活函数，activation function)。它们主要的特点就是通过不同的参数和其它曲线的结合能够转换模拟任何的曲线，越灵活的曲线就越适合做激活函数。有分别Soft Plus,Rectified Linear Unit, Sigmoid，Tanh函数的基本曲线趋势。

一般的神经网络有多层，并且更加的复杂。在输入和出处层之间的每一层都称之为中间层。每一条线和对应的激活函数可以简化为下图的过程，输入先*(-34.4)再加2.14再作为激活函数的输入，得到输出结果，作为下一层的输入。

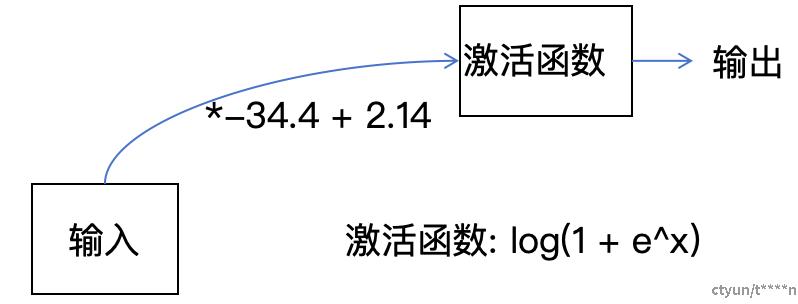
图. 单个激活函数的具体运算逻辑

增加激活函数和分支，可以通过两个简单的激活函数去拟合的绿色的曲线。

2 梯度下降算法

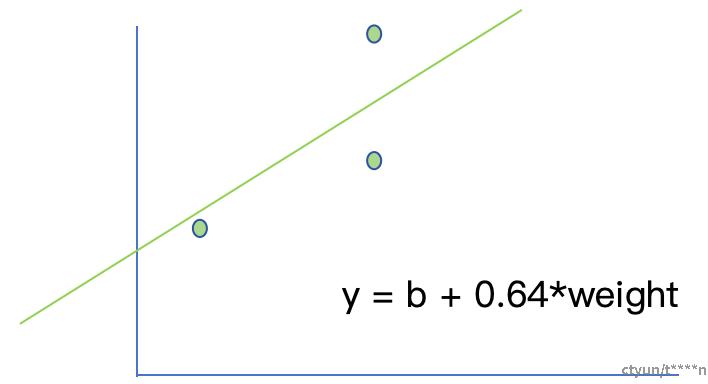
图. 使用直线函数预测点集

如图我们对现有的三个样本数据点，求它的预测直线。其中这个直线我们暂时固定一个斜率参数为0.64,只训练一个参数就是截距（intercept,b)。带变量b的误差函数如下。

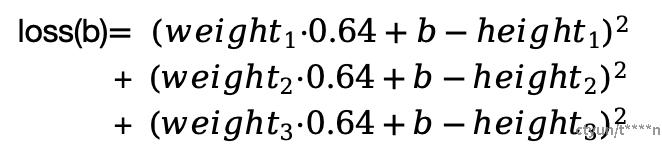
图. 损失函数公式

比如当截距为0的时候误差值为3.1。想要得到最好的预测函数，最简单的方法是对每个可能的b值进行计算，当所有的b值中loss(b)最小，那么这个时候得到的函数就是最好的函数。而b值就是我们一个训练得到的参数。但是这种方式计算量大，属于排查式计算。此外，也可以用如下方程用去解b的二次函数的最小值。

这里将介绍一种万能的算法，就是梯度下降算法。它可以让我们不用逐点的去找损失函数的值，也不需要要求这个损失函数是可以直接数学求解的。我们写出损失函数。

图. 双参数损失函数和其导数

求导数函数之后，初始化一个截距值。例如b = 0，这个时候得到的导数函数值就是-5.7。这就代表函数如果b减去-5.7，是非常可能降低loss值的。一般我们会对-5.7乘上一个学习率，比如0.1。那么本次可以b - (-5.7)·0.1得到新的b值。反复的进行这个过程，可以发现梯度大，它跑得快，梯度小就跑得慢。一般而言，循环不是无限制的，一般循环的次数是有限制的，超过一定的次数就会停止。或者当计算的梯度已经很小了，也就是步长很少了，也可以作为结束的条件。

举例一个最简单的例子，y=x^2,我们为了寻找函数的最低点，我们计算梯度函数（导数）为y=2x，如果当前点在-1处，那么-1*2=-2, 反向就是2，也就是说当前节点应该向右边走是降低函数值的方向。

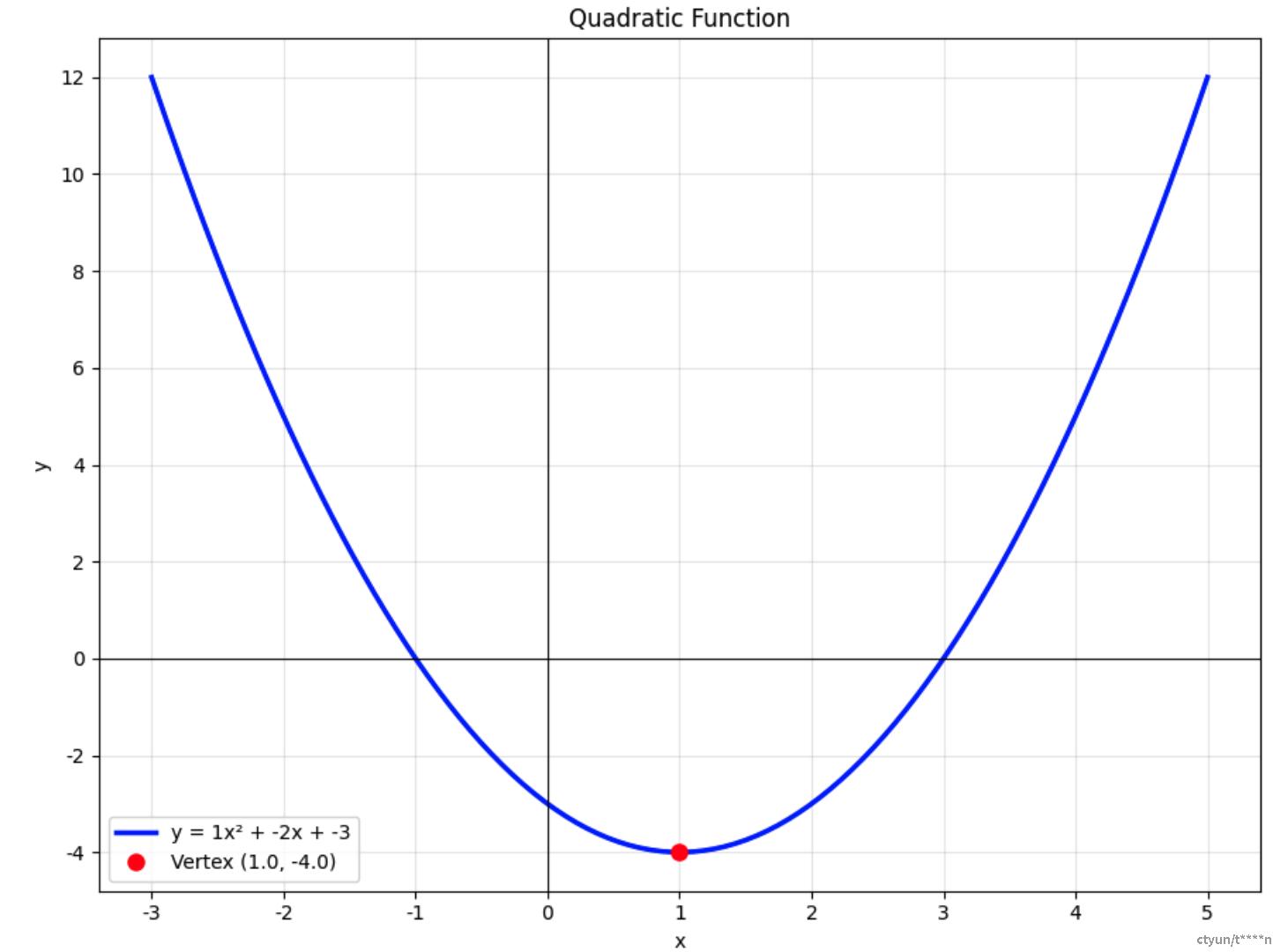
图. y=x^2函数曲线

以上是一个参数，拓展到两个参数也是一样的，考虑上斜率也是训练的参数之一。这个时候这个损失函数就是一个3D图片。一个x,y轴是截距和斜率，z就是损失函数的值。我们目标是求最小值。当然也有数学的解法，但是我们还是可以用梯度下降的办法，因为梯度下降算法是可以拓展的n个参数的。计算偏导的时候，就把另外一个作为常数带入就可以。

图. 双参数的损失函数和其导数公式

有了损失函数关于每个参数的梯度函数之后，就可以算初始点的梯度（例如1,1）。然后每个参数都按照类似的梯度*学习率去调整这个参数得到新的学习到的参数。这个时候直线就会旋转+移动的调整一次。如果是1,1那么代表斜率可以减少1*学习率，截距也可以减少1*学习率。如果有n个参数的时候，整个过程是一样的。虽然还存在很多的其他的损失函数，但是计算梯度，训练参数的过程也是一样的。另外我们这里演示的损失函数是把所有的点都考虑进去了，但是实际的时候每次算梯度的时候，损失函数都可以随机的选择一部分点就可以。比如我们的样本集合有1000个点，我们并不需要每次计算损失函数都用上1000个点，每次用上10个（batch_size），然后计算梯度更新参数。

神经网络反向传递算法

链式求导法则

多级链式求导法则，例如定义了g(x)和f(x) 函数

f(x) = (2x - 1)^2, g(x) = 2x - 1

对于f(x)的求导可以推导为如下:

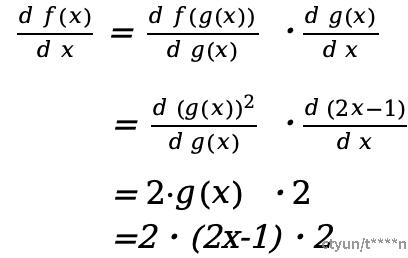
神经网络的反向传递

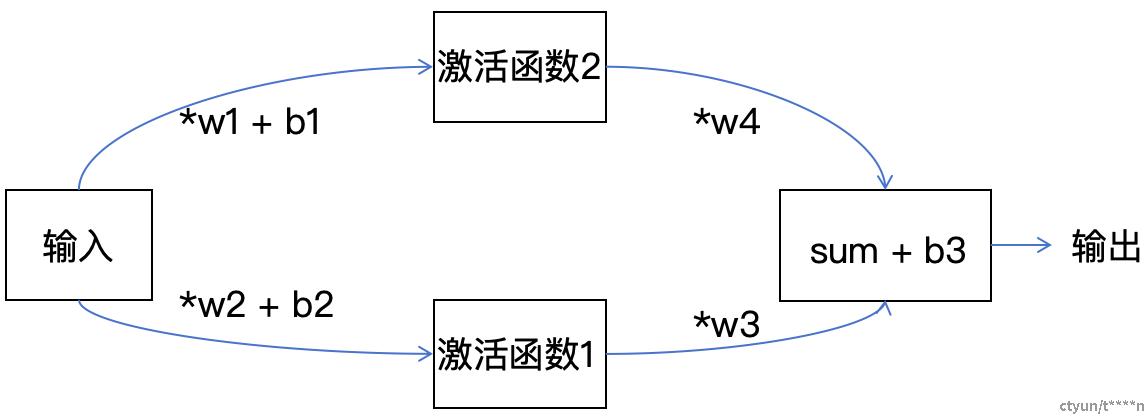
图. 神经网络参数结构

这里有总共7个参数，我们需要求解每一个参数的梯度函数。然后计算每个参数在当前位置的梯度值。每次使用1个数据作为损失函数，定义损失函数为

1 可以看到它和前向计算区别在于，前向计算想算出后面的数据的时候必须先算出它的前面的输入值。并且只有当所有决定当前值的输入值算出来之后才能前进计算。反向计算，如果想算出靠近输入侧的梯度的值的话，那么输出侧计算的导数值是可以直接利用的，只要右侧的参数的梯度值算出来了。那么左侧的梯度值也就出来了。

2 反向计算的时候会使用大量的前向计算的结果，例如标红的语句就会使用到输入1。所以前向计算的每一层的输入输出是需要保存的，而中间的那个激活函数的值不用保存。