算法基础之回溯（C++示例）

回溯法（BackTracking）也叫试探法，是一种选优搜索法，按选优条件向前搜索，以达到目标。若探索到某一步，发现原先选择并不优或达不到目标，就退回一步重新选择，这种走不通就退回再走的技术为回溯法，而满足回溯条件的某个状态的点称为“回溯点”。

回溯算法类似于枚举的过程，当搜索时遇到不满足条件，回退到上一个，尝试别的路径。

回溯法从问题本身出发，寻找可能实现的所有情况。和穷举法的思想相近，不同在于穷举法是将所有的情况都列举出来以后再一一筛选，而回溯法在列举过程如果发现当前情况根本不可能存在，就停止后续的所有工作，返回上一步进行新的尝试。

回溯法常与和递归法结合使用，在回溯法中可以看到有递归的身影。

八皇后问题、迷宫问题是回溯算法的应用场景。

 

例1、列举集合 {1,2,3} 中所有子集的问题

这个问题就可以使用回溯算法。从集合的开头元素开始，对每个元素都有两种选择：取还是舍。当确定了一个元素的取舍之后，再进行下一个元素，直到集合最后一个元素。其中的每个操作都可以看作是一次尝试，每次尝试都可以得出一个结果。将得到的结果综合起来，就是集合的所有子集。

源码如下：

#include <stdio.h>
//设置一个数组，数组的下标表示集合中的元素，所以数组只用下标为1，2，3的空间
int set[5];
//i代表数组下标，n表示集合中最大的元素值
void PowerSet(int i,int n){
    //当i>n时，说明集合中所有的元素都做了选择，开始判断
    if (i>n) {
        for (int j=1; j<=n; j++) {
            //如果树组中存放的是 1，说明在当初尝试时，选择取该元素，即对应的数组下标，所以，可以输出
            if (set[j]==1) {
                printf("%d ",j);
            }
        }
        printf("\n");
    }else{
        //如果选择要该元素，对应的数组单元中赋值为1；反之，赋值为0。然后继续向下探索
        set[i]=1;PowerSet(i+1, n);
        set[i]=0;PowerSet(i+1, n);
    }
}
int main() {
    int n=3;
    for (int i=0; i<5; i++) {
        set[i]=0;
    }
    PowerSet(1, n);
    return 0;
}

运行结果如下：

1 2 3
1 2
1 3
1
2 3
2
3

 

例2、八皇后问题

该问题由国际西洋棋棋手马克斯·贝瑟尔于 1848 年提出：在 8×8 格的国际象棋上摆放八个皇后，使其不能互相攻击，即任意两个皇后都不能处于同一行、同一列或同一斜线上，问有多少种摆法。其中一种放法（0代表皇后）：

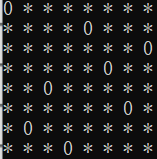
算法解决思路：

1. 从棋盘的第一行开始，从第一个位置开始，依次判断当前位置是否能够放置皇后，判断的依据为：同该行之前的所有行中皇后的所在位置进行比较，如果在同一列，或者在同一条斜线上（斜线有两条，为正方形的两个对角线），都不符合要求，继续检验后序的位置。
2. 如果该行所有位置都不符合要求，则回溯到前一行，改变皇后的位置，继续试探。
3. 如果试探到最后一行，所有皇后摆放完毕，则直接打印出 8*8 的棋盘。最后一定要记得将棋盘恢复原样，避免影响下一次摆放。

源码如下：

#include<iostream>
using namespace std;

int count = 0;
int chess[8][8] = {0};

void Print(){
	printf("解法%d：\n", count);
	for(int i = 0; i < 8; i++){
		for(int j = 0; j < 8; j++){
			if(chess[i][j] == 1)
				cout << "0 ";//皇后
			else cout << "* ";
		}
		cout << endl;
	}
	cout << endl;
}

bool notDanger(int row, int col){
	int i, j;
	for(i = 0; i < 8; i++){	//检查列 
		if(chess[i][col] == 1)
			return false;
	}	
	for(i = row, j = col; i >=0 && j >=0; i--, j--){	//左对角线 
		if(chess[i][j] == 1)
			return false;
	}	
	for(i = row, j = col; i >= 0 && j < 8; i--, j++){	//右对角线 
		if(chess[i][j] == 1)
			return false;
	}	
	return true;
}

void EightQueen(int row){
	if(row > 7){	//8行遍历结束 
		count++;
		Print();
		return;
	}
	for(int col = 0; col < 8; col++){	//对第row行的每一列尝试赋值 
		if(notDanger(row, col)){
			chess[row][col] = 1;
			EightQueen(row+1);	//每行只有一个 
			chess[row][col] = 0; //复原 
		}
	}
}

int main(){
	EightQueen(0);
	printf("共%d种解法\n", count);
	return 0; 
}

运行效果如下：

 

例3、迷宫问题

问题描述

迷宫问题是回溯法的一种应用。迷宫问题的描述为：假设主体放在一个迷宫地图入口处，迷宫中有许多墙，使得大多数的路径都被挡住而无法行进。主体可以通过遍历所有可能到出口的路径来到达出口。当主体走错路时需要将走错的路径记录下来，避免下次走重复的路径，直到找到出口。主体需遵从如下三个原则：

    一次步进只能走一格；
    遇到路径堵塞后，退后直到找到另一条路径可行；
    走过的路径记录下来，不会再走第二次。

先创建一个二维数组Map[][]并进行初始化，Map[i][j]=1表示该位置是墙体，Map[i][j]=0 表示该位置是路。假设主体（人、动物或者飞行器）放在一个迷宫地图入口处，按上述原则在寻找出口路径。

源码如下：

#include <iostream>
using namespace std;

# define UP 0 //定义上
# define DOWN 1 //定义下
# define LEFT 2 //定义左
# define RIGHT 3 //定义右

# define MAP_MAX 10 //定义最大地图
int map[MAP_MAX][MAP_MAX] =
{
    {1,1,1,2,1,1,1,1,1,1},
    {1,0,0,0,1,0,1,1,1,1},
    {1,0,1,0,1,0,1,1,1,1},
    {1,0,1,0,0,0,0,0,1,1},
    {1,0,1,0,1,1,0,1,1,1},
    {1,0,1,0,0,1,0,1,1,1},
    {1,0,1,1,0,1,0,0,0,1},
    {1,0,1,1,1,1,1,1,0,1},
    {1,0,0,0,0,0,0,0,0,1},// 
    {1,1,1,1,1,1,1,1,0,1}//1是墙 ，0是路 ；出发点标2【注*】 
};

/*
    打印地图
*/
void print_map()
{
    int i,j;
    char emt[]=" #R";
    //定义显示的数组
    putchar(' ');
    for(j=0; j<MAP_MAX; j++)
    {
        printf(" %d", j);
    }
    putchar('\n');
    for(i=0; i<MAP_MAX; i++)
    {
        printf("%d ", i);
        for(j=0; j<MAP_MAX; j++)
        {
            printf("%c ", emt[map[i][j]]);
        }
        putchar('\n');
    }
}

/*
    单纯的移动，并且进行值的改变
*/
void move(int &x, int &y, int d)
{
    switch(d)
    {
    case UP:
        x--;
        break;
    case DOWN:
        x++;
        break;
    case LEFT:
        y--;
        break;
    case RIGHT:
        y++;
        break;
    }
}
/*
    检查下一步是否可行
    x，y点开始
    d方向
*/
int inspect(int x,int y,int d)
{
    // printf("%d %d %d\n", x,y,d);
    move(x,y,d);

    if(x<0 || y<0|| x>=MAP_MAX || y>=MAP_MAX || map[x][y]!=0)
    {
        return 0;
    }

    return 1;
}

void print_pro(int s[2], int e[2], int n){
    /*打印过程*/
    putchar('\n'); //
    printf("当前:(%d, %d) 终点:(%d, %d) 步数:%d\n", s[0],s[1],e[0],e[1],n);
    print_map();
}

/*
    走迷宫（递归回溯所有可能都走）
    s是开始坐标
    e是结束坐标
    n当前第几步
*/
int mazes(int s[2],int e[2],int n)
{
    if(s[0]==e[0] && s[1]==e[1]){
        print_pro(s,e,n);
    }

    int i;
    for(i=0; i<4; i++)//向四个方向同时走
    {
        if(inspect(s[0],s[1],i))//检查i方向是否可以行得通
        {
            int tx = s[0], ty = s[1];//设置临时变量，防止数据混乱
            move(tx,ty,i);//向i方向移动一步
            map[tx][ty] = 2;//标记已走
            int ta[2] = {tx,ty};//传值变量
            mazes(ta,e,n+1);
            map[tx][ty] = 0;//取消标记
        }
    }
}

int main()
{
    int n = 0;//初始步数
    int s[2] = {0,3};//s初始位置【注*】 
    int e[2] = {9,8};//e终止位置 
    mazes(s,e,n);//调用走迷宫
    putchar('\n');
    return 0;
}

运行效果如下：