前缀和算法总结:
常规的前缀和分为两种(也是练习1、2):
-
一维前缀和:比较简单,在我们需要快速的算出某一数组中的数据时,可以想想是否能使用前缀和,它的使用条件:
- 一维数组
- 求数组中任意连续的值
- 对于满足上述条件后就能考虑使用前缀和数组
- 其中前缀和数组存储
dp[ i ]的是:从1~ i区域内的元素值之和 - 其中下标从1开始算,每次创建的数组大小为 n + 1 保证从 1 开始(从1开始是因为: 计算 dp[i] 需要使用 dp[i - 1],假设 i 不从1开始,若 i 为0,就会越界访问)
- 具体当我们拥有了一个前缀和数组dp后,使用前缀和数组算出结果,当要求
r ~ l这段区间时它的计算方法就是:dp[ r ] - dp[ l -1 ]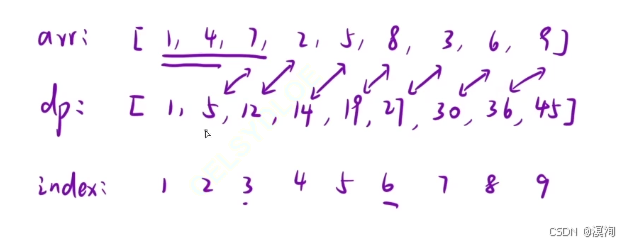
-
二维前缀和:
-
条件类似:二维数组,当要求某一块区间的值时 可以考虑使用二维前缀和
-
该二维前缀和数组
dp[ i ][ j ]中存储的是:从(0,0) ~ (i,j)区域的所有元素值的和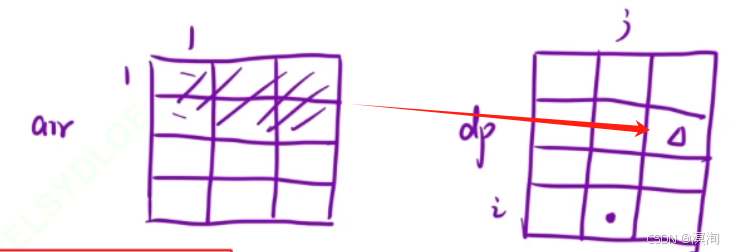
-
使用:对于二维前缀和的使用稍微对比起来有点难度,一般来说需要使用到两个公式
- 计算出二维前缀和数组中的值的公式:dp[ i ][ j ] = dp[ i ][ j - 1] + dp[ i-1 ][ j ] + arr[ i ][ j ] - dp[ i - 1 ][ j - 1 ]
对于该公式,切记一定不要死记
通过下图右边图记忆:
理解:当我们我们要求的空间可以分为右边图形中的四块:A、B、C、D,其中假如我们从上往下,从左往右的去填写当前的dp数组时,本质上 A、B、C三个区域的值都是已经算好了的,而对于 D 来说他就是自身当前位置的值 arr[ i ][ j ],所以这样我们就能得出上面的公式:
A = dp[ i - 1][ j - 1 ]、B = dp[ i - 1][ j ]、C = dp[ i ][ j - 1 ]、D = arr[ i ][ j ]
- 使用二维前缀和公式快速算出任意两点
(x1,y1) ~ (x2,y2)区域的公式:dp[ x2 ][ y2 ] - dp[ x1 - 1 ][ y2 ] - dp[ x2 ][ y1 - 1 ] - dp[ x2 ][ y1 - 1] + dp[ x1 - 1][ y1 - 1 ]
而对于这个公式来说同样,也是通过一张图进行记忆:
具体如下就过诉了,这里本质要求的就是 D 区域,如何通过 提前准备好的 二维前缀和数组 求出 D区域的值(同样还是记忆下面右图逻辑即可,必要时画个图)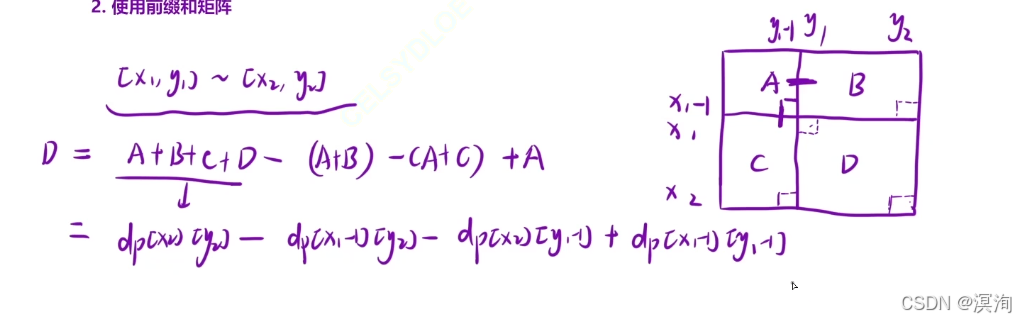
-
-
其中前缀和只是个思想,它使用一个数组的形式提前存储一段区间的值,其中这个 区间的值的求法,可能并不一样
- 比如存储了
1 ~ i区间的和、 - 存储了
1 ~ i区间的乘积、 - 存储了
1 ~ i区间的某个数的出现个数… - 再或者是一个后缀和(从后往前的记录其中的值)
- 比如存储了
- 始终记住前缀和可以用来求出某一段连续区域的值的思想,后面首先会通过两道简单的题(一维和二维前缀和练手),后面将会逐步递增难度(也就代表这个前缀和中存储的并不是 前缀的和)
- 过程中一般都是求某段连续区域中的某个值,对于感觉大脑不够想的时候一定要画图!通过简单的图示更方便的理解和写出公式
具体训练:
1. 一维前缀和【模板】
题目:
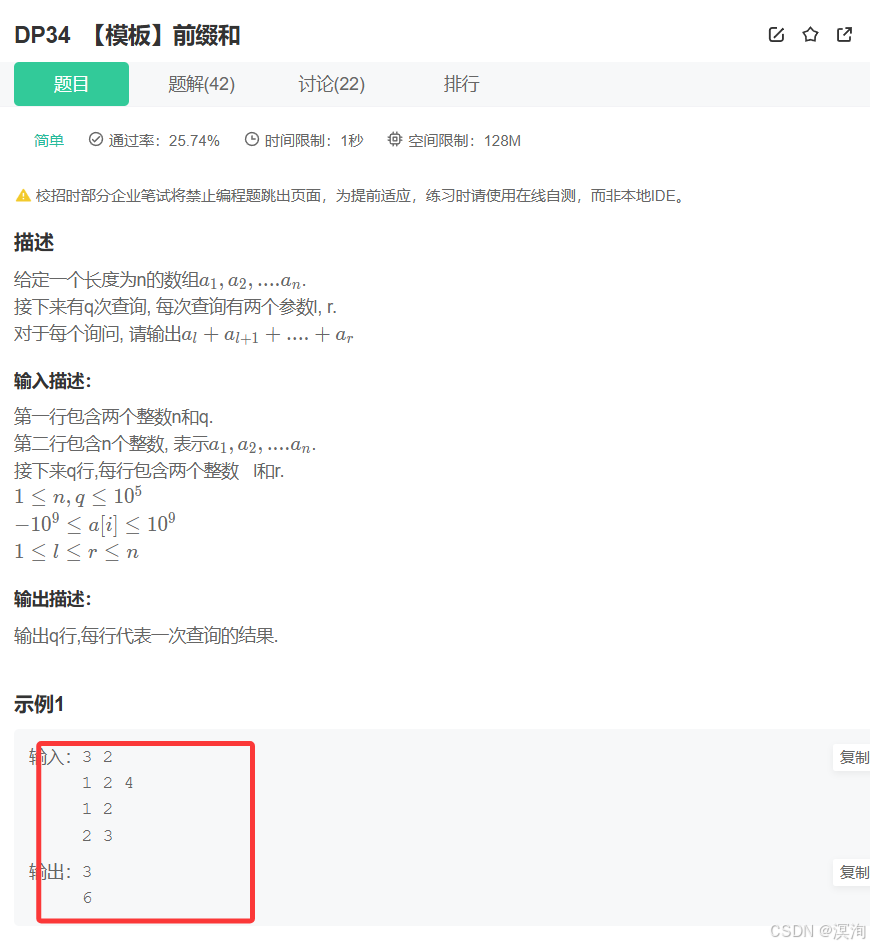
分析题目并提出,解决方法:
结合题目分析:
- 首行是 n :数组个数、q:查询次数
- 第二行是有n个元素的数组的值:…
- 后面有q行,它的值代表查找区间 [左 ~ 右]
- 那么然后输出查询结果
- 例如在下面 1 2 4 数组中查找(1,2)、(2,3)、(1,3) 区间的值,具体如下
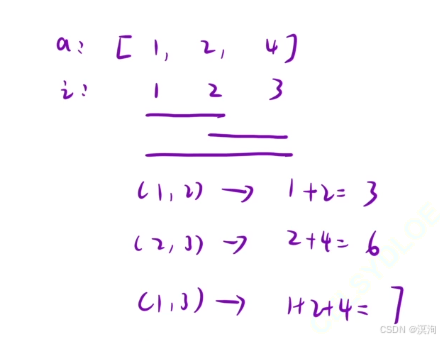
暴力题解:简单的模拟,根据给q次给的left、right下标,并从该区间【left,right】遍历求和得出答案(O(n * q)的时间复杂度)
对于这种连续数组中求和的情况我们一定要想到前缀和:快速求出数组中某一个连续区间的和
前缀和算法到底是什么?
通过实例来解释:
一维前缀和模板:
- 预处理出来一个前缀和数组dp(小动态规划)
- dp[i]:表示的是 1 ~ i 区间所有元素的和(下标从1开始算,每次创建的数组大小为 n + 1 保证从 1 开始)
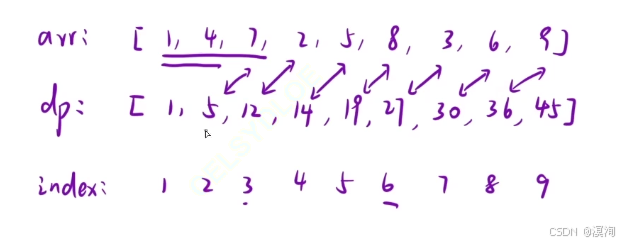
- 并且在计算dp数组的过程中,==dp[ i ] = dp[ i - 1] + arr[ i ]==即可算出(具体分析如上图很好理解),这样更快的求出,不需要每次都遍历真个数组!
- 为什么下标从1开始:因为此处要计算 dp[i] 需要使用 dp[i - 1],i 若为0,就会越界,所以从1开始,这样 即使第一个情况下:1 - 1 = 0 也不会越界
- dp[i]:表示的是 1 ~ i 区间所有元素的和(下标从1开始算,每次创建的数组大小为 n + 1 保证从 1 开始)
- 使用前缀和数组
- 当我们得到一个前缀和数组后,假设有下情况:
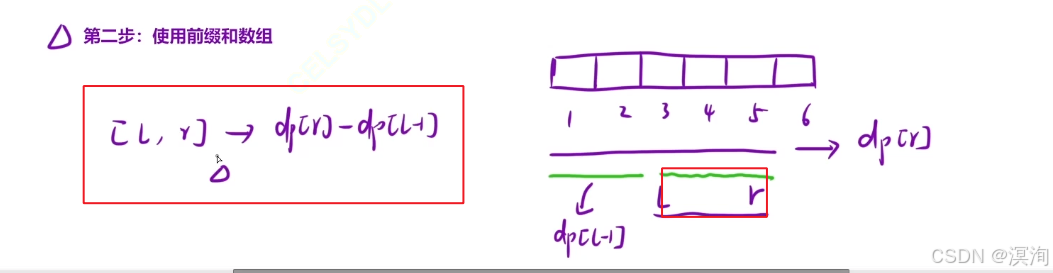
- 当我们要去 l ~ r 情况的值:就能通过快速的减法得到:dp[ r ] - dp[ l -1 ]
- 算法时间复杂度:O(n) + O(q) = O(n)
- 当我们得到一个前缀和数组后,假设有下情况:
题解核心逻辑:
- 根据题目初始化存储好:n,q,数组,查询区域
- 初始化前缀和数组dp
dp[ i ] = dp[ i - 1] + arr[ i ]
- 使用前缀和数组算出结果
dp[ r ] - dp[ l -1 ]
代码:
#include <iostream>
#include <vector>
using namespace std;
int main() {
int n , q;
cin >> n >> q;
long long arr[100010] = {0};//根据题目数量级设置,之前设置超过数量级大小的数组即可
long long dp[100010] = {0};
for(int i = 1; i <= n;i++){//从1开始因为,前缀和需要下标从1开始,留0位置
cin >> arr[i];
}
vector<vector<long long>> lr;//使用vector存储左右区间
lr.resize(q);
for(int i = 0 ; i < q;i++){
int left,right;
cin >> left >> right;
lr[i].push_back(left);
lr[i].push_back(right);
}
//1. 使用一维前缀和快速求值:
//dp[i] = arr[i] + dp[i-1]
for(int i = 1; i <= n;i++){
dp[i] = arr[i] + dp[i-1];
}
for(int i = 0 ; i < q;i++){
// 使用前缀和求值
int l = lr[i][0];
int r = lr[i][1];
cout << dp[r] - dp[l-1] << endl;
}
return 0;
}
2. 二维前缀和【模板】
题目:

分析题目并提出,解决方法:
分析题目的例子并理解:
- 第一行是三个数n,m,q
- n:代表矩阵数据的行数,m代表矩阵列数,q代表请求查询的参数
- 其次n行m列的数就是矩阵数据
- 最后的q行数据代表的是:查询的矩阵的左上角和右下角两点,
- 过程中可以将数据看成每两个为一个矩阵中的xy点,这样就能得到两点(x1,y1)、(x2,y2)
如下数据的第一个查询参数值是 1 1 2 2 那么查询的的两点是 (1,1) ~ (2,2)
最终要求的就是这两点矩阵区间的值(如下图)
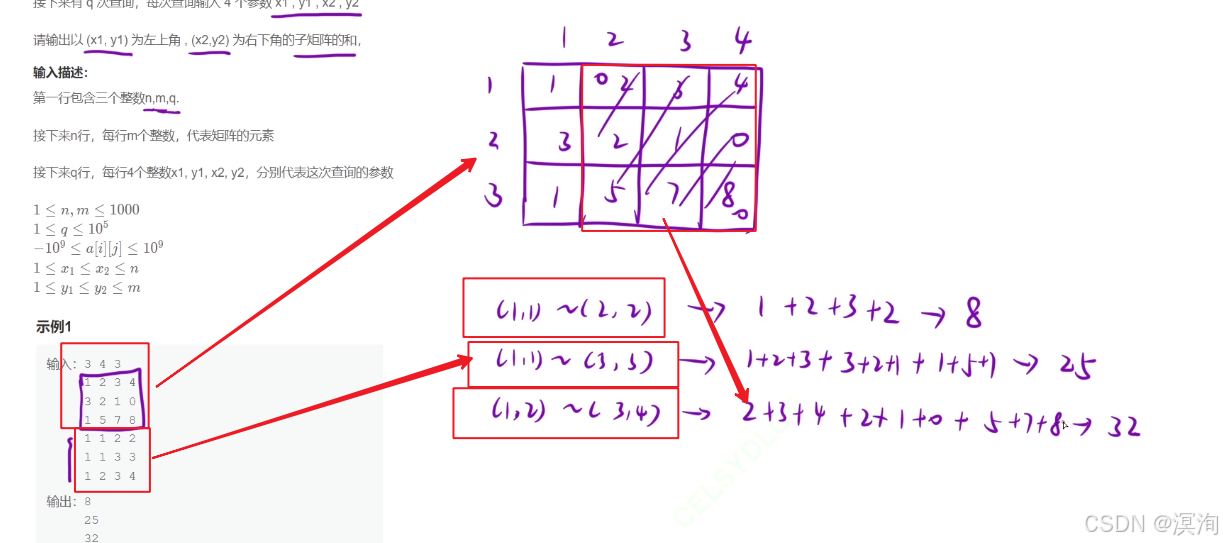
暴力解法:同样是模拟,根据给的两点的确定查询的矩阵的行列,遍历求和即可
二维前缀和模板:
-
预处理处一个前缀和矩阵
- 创建和原处理矩阵同等大小矩阵dp
- 然后对dp中的值进行设置,此处dp内的值和一维前缀和里的值略有不同也更难理解一丢丢,此处二维的是求从 (1,1) ~ (i, i)内这个小矩阵的和,但直接求发现还是表还是得遍历时间复杂度还是比较高,那么在求的过程中就能不能优化下?可以通过利用之前的dp矩阵得出快速求dp[ i ][ j ] = dp[ i ][ j - 1] + dp[ i-1 ][ j ] + arr[ i ][ j ] - dp[ i - 1 ][ j - 1 ]
具体如下图(注意记住左下角那张分析图,能很好的帮助你理解和记忆公式):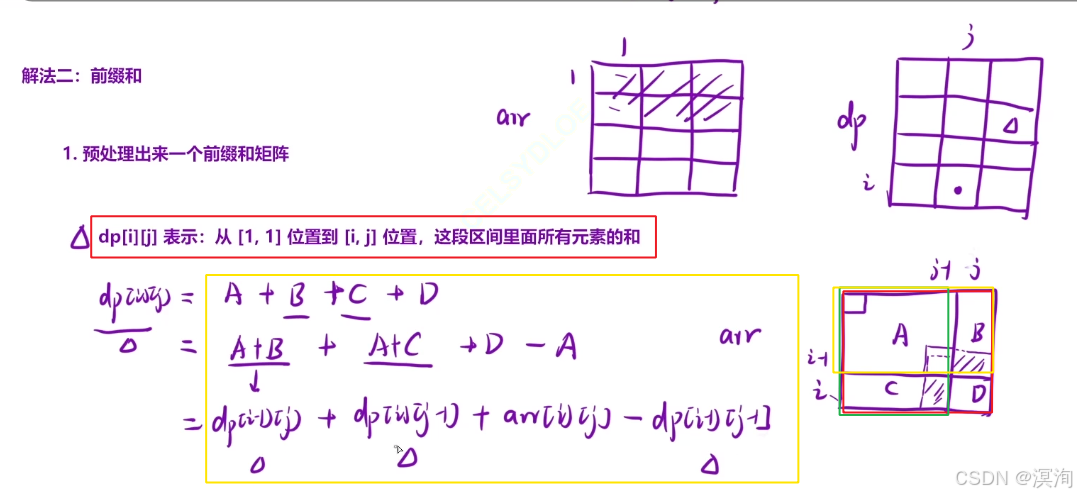
-
如何使用前缀和矩阵快速取出要求的指定矩阵中的值
- 方法类似通过对原矩阵进行分割,通过许多前面算好的矩阵中的值来快速的计算出当前的值,其中划分的步骤很关键,一定要好好理解。
- 为什么划分,为了利用之前的值,并且在划分的过程中使用了更简洁的图来更方便理解!
- 那么如何使用求出指定的区域能,如下图求D区域,找到左下角点和右下角点,分析该如何划分区间,本质就是要考虑两点的关系
- 首先我们可以记住若左上角刚好在整个矩阵的左上角,那么要求的值就是d[x2][y2]的区间的大小
- 那么当左上角不在整个原矩阵最左上角时,对于右下角的值来说需要将左上角之外的多余的值给清除(这样记忆更加的好通过图来记忆公式!)
最终划分出来后如下图(注意记住好左边那张分析图,通过这理解这张图帮助你快速理解和记忆公式)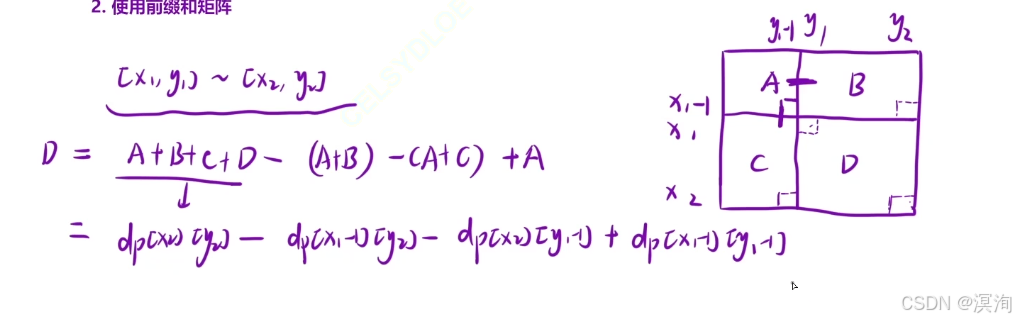
5.最终得出的所要求的区域值就是: dp[ x2 ][ y2 ] - dp[ x1 - 1 ][ y2 ] - dp[ x2 ][ y1 - 1 ] - dp[ x2 ][ y1 - 1] + dp[ x1 - 1][ y1 - 1 ]
题解核心逻辑:
- 根据题目初始化存储好:n,m,q、矩阵,查询的两点
- 初始化前缀和矩阵dp
dp[ i ][ j ] = dp[ i ][ j - 1] + dp[ i-1 ][ j ] + arr[ i ][ j ] - dp[ i - 1 ][ j - 1 ]
- 使用前缀和数组算出结果
dp[ x2 ][ y2 ] - dp[ x1 - 1 ][ y2 ] - dp[ x2 ][ y1 - 1 ] - dp[ x2 ][ y1 - 1] + dp[ x1 - 1][ y1 - 1 ]
代码:
#include <iostream>
using namespace std;
#include <vector>
int main() {
int n, m, q;
cin >> n >> m >> q;
long long arr[1010][1010] = {0};
long long dp[1010][1010] = {0};
for (int i = 1; i <= n;
i++) { //从1开始因为,前缀和需要下标从1开始,留0位置
for (int j = 1; j <= m; j++) {
cin >> arr[i][j];
}
}
vector<vector<long long>> lr;//使用vector存储左右区间
lr.resize(q);
for (int i = 0 ; i < q; i++) {
int x1, y1, x2, y2;
cin >> x1 >> y1 >> x2 >> y2;
lr[i] = {x1, y1, x2, y2}; //使用initiate
}
//初始化dp值
for (int i = 1; i <= n;
i++) { //从1开始因为,前缀和需要下标从1开始,留0位置
for (int j = 1; j <= m; j++) {
dp[i][j] = arr[i][j] + dp[i - 1][j] + dp[i][j - 1] - dp[i - 1][j - 1];
// dp[i][j] = A + B + C + D = D + (A + B) + (A + C)- A
}
}
//使用dp值:
for (int i = 0 ; i < q; i++) {
int x1 = lr[i][0], y1 = lr[i][1], x2 = lr[i][2], y2 = lr[i][3];
cout << dp[x2][y2] - dp[x1 - 1][y2] - dp[x2][y1 - 1] + dp[x1 - 1][y1 - 1] << endl;
// D = (x2y2) - B - C - A = (x2y2) - (A+B) - (A+c) + A
}
return 0;
}
// 64 位输出请用 printf("%lld")
3. 寻找数组的中心下标
题目:
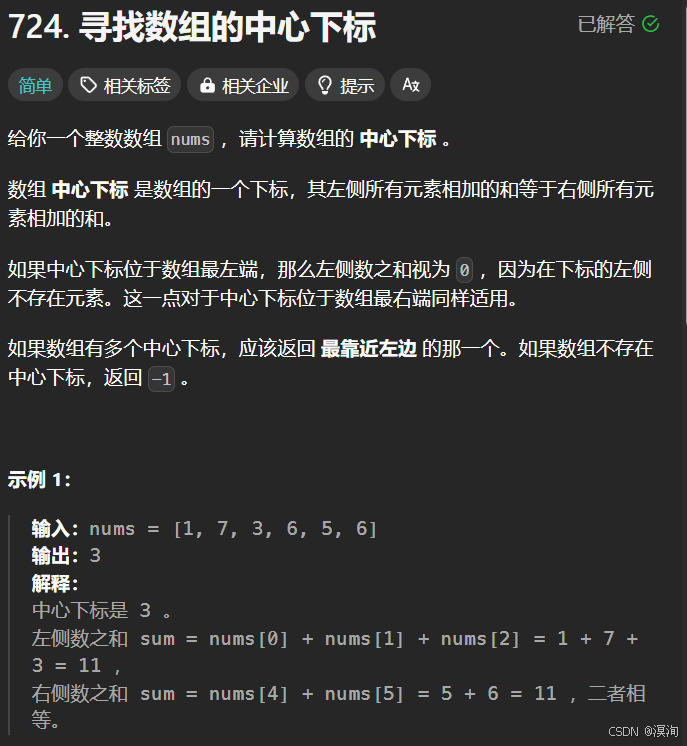
分析题目并提出,解决方法:
分析题目,不难理解示题1的3结果由来: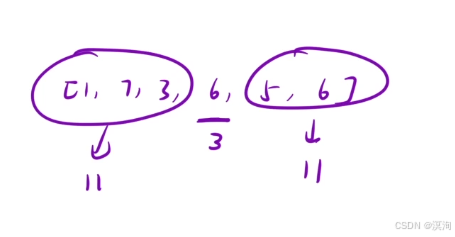
两种特殊情况:
- 当没有结果时返回 -1
- 默认最左边元素的左半区为0,最右边元素的右边区也为0
- 并且当结果有多个的时候返回最左边的结果
本质所要求的是如下图( i 的左边区间 = i 的右边区间的 i ):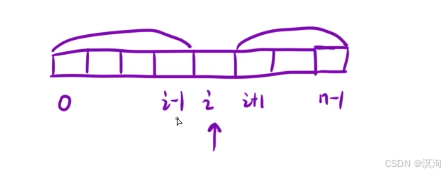
本题本质还是在连续数组中找值,那么我们就能使用前缀和思想:
- 提前预处理好数据到dp中
- 现在需要求的就是 ( 0,i - 1 )、( i + 1,n -1) 这两区间的值

- 前缀和数组:f [ i ] = f [ i - 1 ] + num [ i - 1 ]
- 后缀和数组: g [ j ] = g [ i + 1 ] + num[ i + 1 ]
- 现在需要求的就是 ( 0,i - 1 )、( i + 1,n -1) 这两区间的值
- 利用提前处理好的数组,进行题目要求的判断
- 假设要判断 i 位置的点是否符合条件 那么就等于判断
f[ i ] == g[ i ]
- 假设要判断 i 位置的点是否符合条件 那么就等于判断
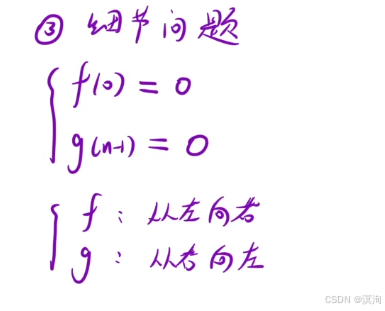
题解核心逻辑:
- 创建前缀和数组f:0 ~ i -1、后缀和数组g:i + 1 ~ n - 1
- 通过前面的公式预处理
f[ i ] = f[ i - 1 ] + arr[ i - 1 ]g[ i ] = g[ i + 1 ] + arr [ i + 1]
- 最后遍历数组,找到
f[ i ] == g[ i ]处
更多细节见具体代码:
class Solution {
public:
static const int CAP = 1e4 + 10;
int pivotIndex(vector<int>& nums) {
//分析出本题:本质可以通过提前预处理好数组的值来快速计算:前缀和思想
//使用前缀和f数组 和 后缀和g数组 存储连续数组的数据
int f[CAP] = {0};int g[CAP] = {0};
int n = nums.size();
//1. 预处理数组
//前缀和,f[i] = 0 ~ i - 1
for(int i = 1; i <= n;i++){
f[i] = f[i-1] + nums[i - 1];//算出 0 ~ i - 1的和
}
//后缀和,g[i] = i + 1 ~ n - 1
for(int i = n - 2;i >= 0;i--){
g[i] = g[i+1] + nums[i+1];//g [i] 存储的是 i + 1 ~ n - 1的值
//所以当 i = n - 2 存储的就是 n - 1 ~ n - 1的值
}
//2. 使用预处理数组进行判断
for(int i = 0; i < n ;i++)
if(f[i] == g[i]) return i;
return -1;
}
};
4. 除自身以外数组的乘积
题目:
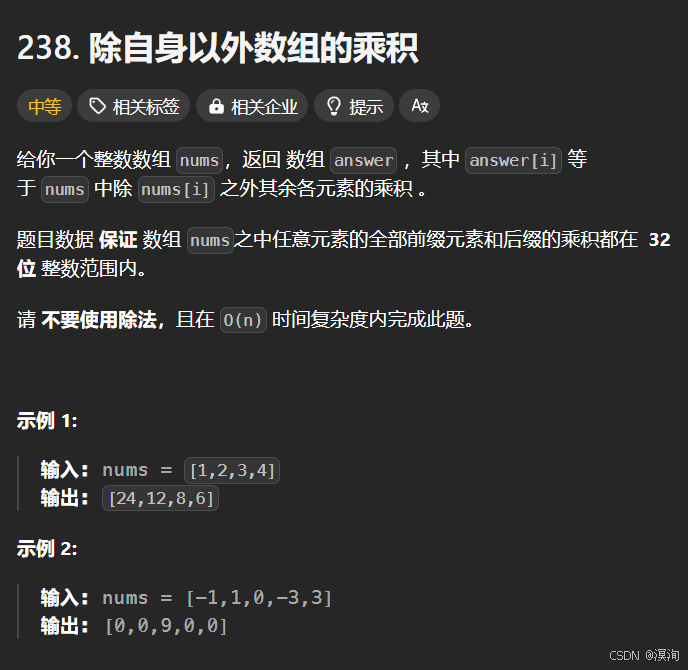
分析题目提出解决方法:
本题本质其实和上一题一样,只不过,本题并不是前缀和,而是前/后 缀积
前缀积、后缀积的算法:
本质也就是将 加法 变成了 乘法(具体如下)
题解核心逻辑:
基本同上就略了
class Solution {
public:
static const int CAP = 100010;
vector<int> productExceptSelf(vector<int>& nums) {
int f[CAP] = {1};//这里是乘法所以等于1
int g[CAP];
int n = nums.size();
g[n - 1] = 1;
//处理前缀积
for(int i = 1; i <= n;i++){
f[i] = f[i-1] * nums[i-1];
}
//处理后缀积
for(int i = n - 2; i >= 0;i--){
g[i] = g[i+1] * nums[i+1];
}
//使用预处理好的数组:
vector<int> ans(n);
for(int i = 0; i < n ;i++){
ans.push_back(g[i] * f[i]);
}
return ans;
}
};
5. 和为 K 的子数组
题目:
分析题目提出解决方法:
通过例子分析,题目的目的: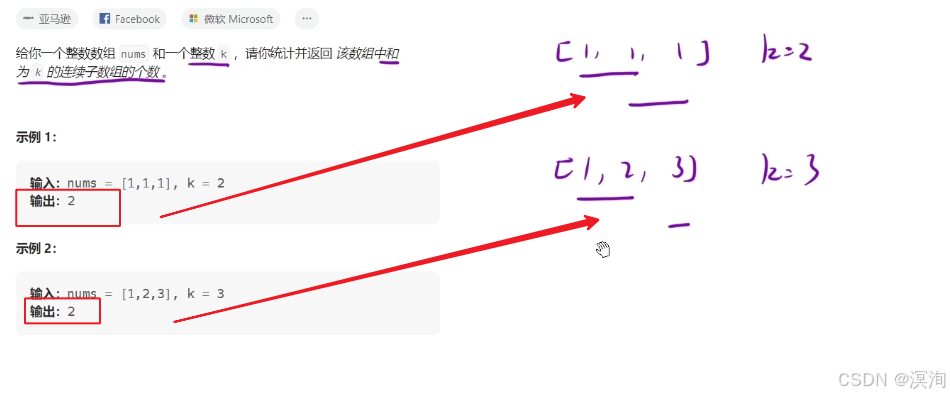
暴力解法,就是枚举所有情况(复杂度O(N2))
分析如何快速找到连续子数组中的值为 k 的子数组
-
先画一个简单的图来分析:不难发现,若要找以 i 结尾的连续子数组,本质是在
0 ~ i - 1这个区间找一个值为sum[ i ] - k的值有多少个
(具体如下图,找k长度的区间,可以转换为找sum[ i ] - k 区间的个数,这样就和前面关联了)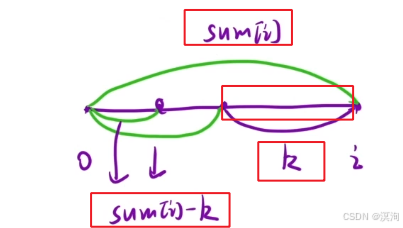
-
那如何快速的找出 0 ~ i - 1 区间中 sum[ i ] - k 的个数呢?对于这种数值的查找,可以通过hash表提前存储好
-
具体hash的使用是:每当查找完一个区间后,将当前下标的 sum[ i ] - k 的值存入hash中
-
特殊处理:当
sum[ i ] == k时,查找的区间就是0 ~ -1中找 0(sum[i] - k)这本质是不存在的,所以需要提前将hash[0] = 1,因为区间不存在就无法查找,而此时sum - k = 0,所以就代表自己这个区间就是符合条件的。 -
其他细节如下:

题解核心逻辑:
- 使用hash表不断记录 0 ~ i - 1 区间中所有sum的情况(因为通过前面的sum情况知道有多少数据为 sum[i] - k)
- 开始遍历数组,判断是否有值等于当前的 sum - k,若有则代表有符合长度的以i结尾的子数组然后记录个数即可
class Solution {
public:
int subarraySum(vector<int>& nums, int k) {
//存储 0 ~ i - 1 的sum[i] - k个数(注意这本质存的还是0 ~ i - 1区间中每个元素的sum,只是为了找某个值的 sum = 当前sum - k )
unordered_map<int,int> hash;
hash[0] = 1;//特殊处理
int count = 0,sum = 0;
for(int i = 0;i < nums.size();i++){
sum += nums[i];//
if(hash.count(sum - k))
count += hash[sum - k];
hash[sum]++;
}
return count;
}
};
在本题中同样用到了,前缀和的思想,其中加上了hash来代替前缀和,通过hash代替前缀和中记录前面子数组值,从而实现即记录了子数组的值,右记录了相同子数组值的个数
6. 和可被 K 整除的子数组
题目:

分析题目提出解决方法:
本题和上题类似,本题求的是连续子数组和能被k整除个数(上题是找等于k的个数)
直接本题通过例就能看懂了,并且暴力解法也和上类似就不过诉了!
同余定理
同余定理:通过公式理解(具体如下)(a - b) / p = k (余0) -> a % p = b % p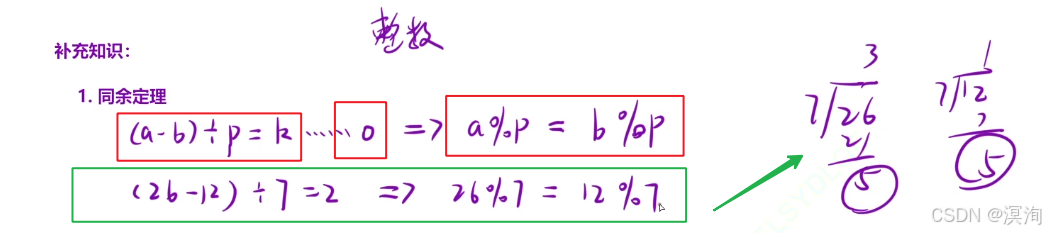
证明过程…:
c++ / java 的负数取模的结果以及修正
- 负数 % 正数 = 负数 -> 修改为正数:
- 将值a =(a % p + p)% p(这个公式保证了值无论是 整数还是负数最终都能变成正确取余后的整数)
题解核心逻辑:
同上题一样将数组抽象:
若要再0 ~ i - 1区域中查找一个以i结尾的子数组的和的余数 = 0 的子数组个数
得到下图左边的公式:(sum - x) % k = 0
其中就要使用到同余定理得到:sum % k = x % k(从而得到了 x 区域的求法!:sum % k)
所以本题在上题的基础上修改hash中存储的值:存储的就是所有前缀和的余数的个数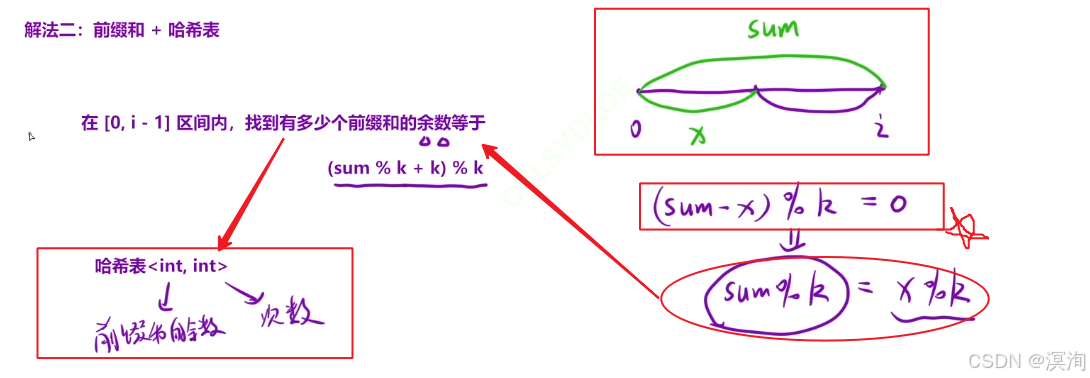
- hash[0] = 1;这里处理的是:当 0 ~ i 区间刚好整除 k,那么 此时 sum % k = 0
class Solution {
public:
int subarraysDivByK(vector<int>& nums, int k) {
unordered_map<int,int> hash;//一个变化的hash:存储 0 ~ i-1 内所有前缀和的余数的个数
hash[0] = 1;//这里处理的是:当 0 ~ i 区间刚好整除 k,那么 此时 sum % k = 0
int count1 = 0,sum = 0;
for(int i = 0; i < nums.size();i++){
sum += nums[i];//前缀和
// cout << sum << " " << sum % k << " ";
if(hash.count((sum % k + k) % k))
count1 += hash[(sum % k + k) % k];//查找 sum % k的个数
// cout << hash[sum % k] << " "<< count1 << endl;
hash[(sum % k + k) % k]++;//添加 / 创建 sum % k的个数
}
return count1;
}
};
7. 连续数组
题目:

分析题目提出解决方法:
本题关键:将 0 看出 -1
相信如果从上往下做到了该题,那么你已经具备了一定能力了,下面我就不过多叙述; ,还是那句话遇到难题一定要画图分析
具体分析如下图: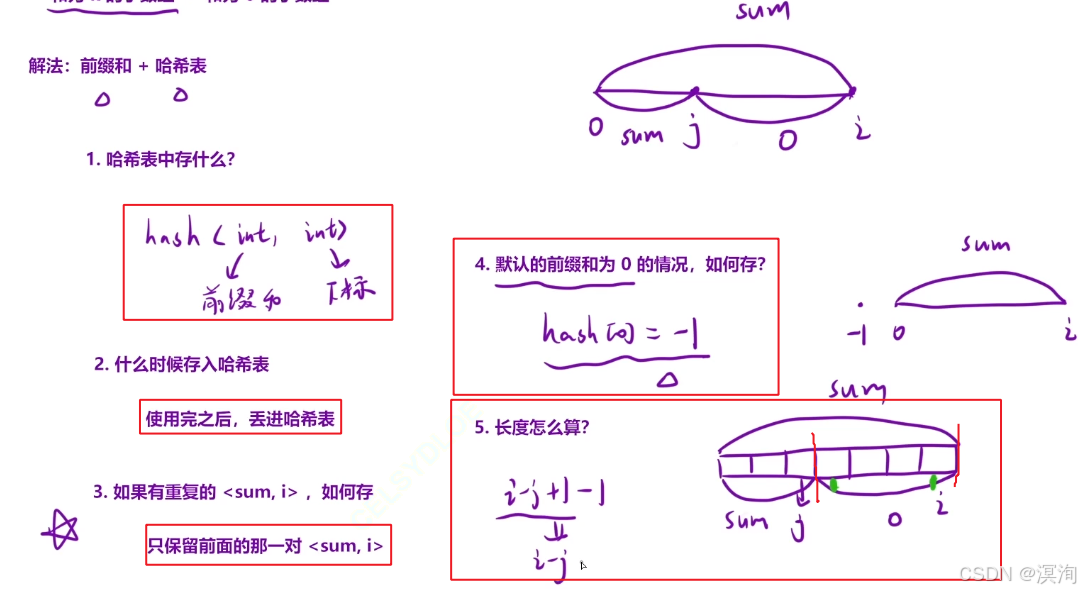
题解核心逻辑:
class Solution {
public:
int findMaxLength(vector<int>& nums) {
//将 0 看出 -1
//求连续子数组中和为0的个数
unordered_map<int,int> hash;//存储前缀和的值和下标
// 0 ~ i sum
// k = 0, 找前缀和等于 sum - 0 = sum 的个数
hash[0] = -1;//此处特殊处理:当 0 ~ i 区间为0的情况下 sum就为0,那么查找的区间是不存在的,所以需要提前设置
int sum = 0,count =0;
int maxlen = 0;
for(int i = 0; i < nums.size();i++){
sum += (nums[i] == 1 ? 1 : -1);
// hash[sum]
if(hash.count(sum)){
// cout << sum << " " << hash.count(sum) << " " << hash[sum] <<" ";
maxlen = max(maxlen,i - hash[sum]);
}
if(!hash.count(sum)){//判断是否已经存在,若已经存在则不用再记录了,因为最左区间已经确定
hash[sum] = i;
// cout << sum << " " << hash[sum]<<endl;
}
}
return maxlen;
}
};
8. 矩阵区域和
题目:
分析题目提出解决方法:
一道二维前缀和的题,理解公式轻松解决
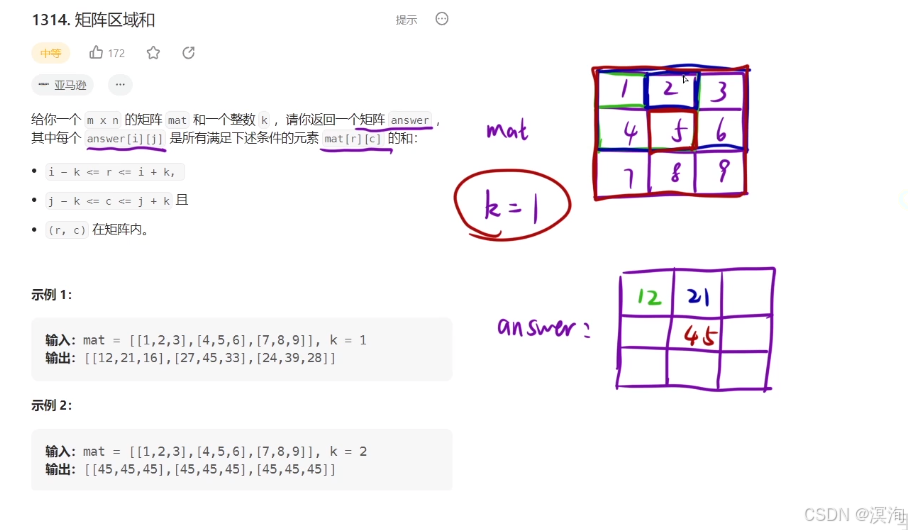
其中注意理解题意:本质就是求以(i,j)为中心的九宫格
分析图如下:
- 其中注意 dp 的下标是从 1 开始的,所以mat中下标都要-1
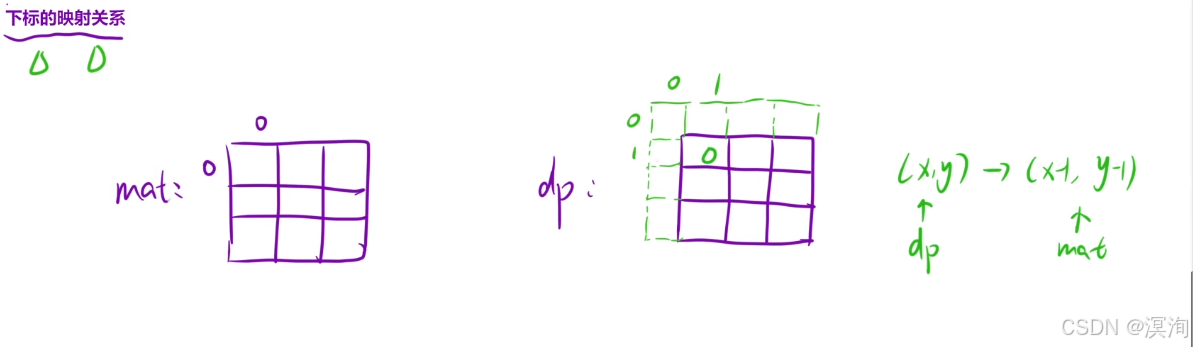
- 二维前缀和模板
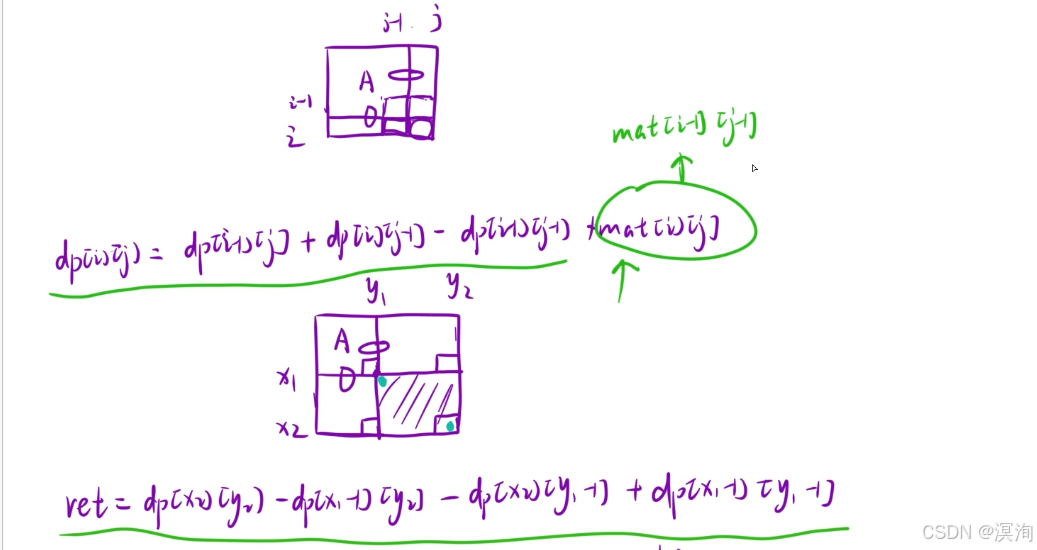
- 而 ans中的小标是从0开始的,所以使用dp时要+1
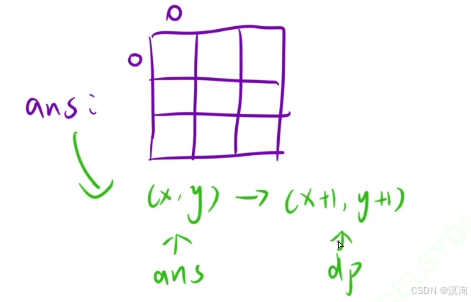
4. 注意越界问题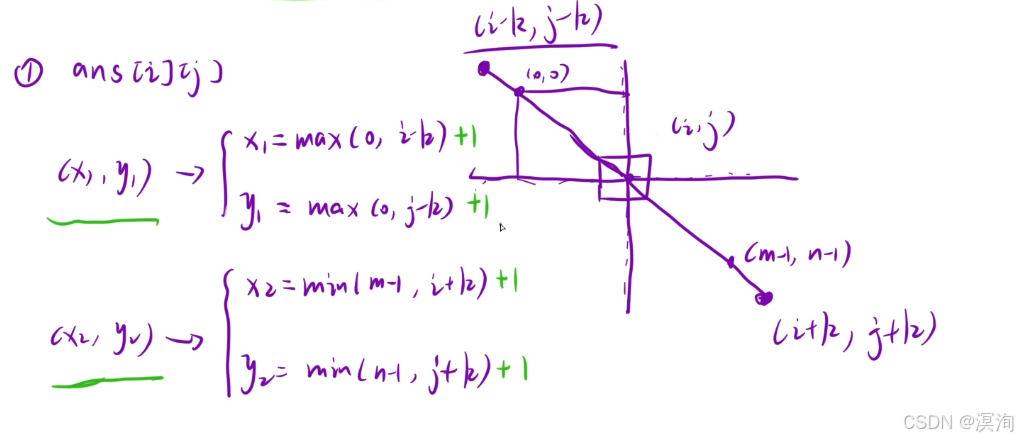
题解核心逻辑:
class Solution {
public:
vector<vector<int>> matrixBlockSum(vector<vector<int>>& mat, int k) {
//很清楚的二维前缀和
int m = mat.size();
int n = mat[0].size();
vector<vector<int>> ans(m,vector<int>(n,0));
//创建dp表,并预处理得到所有 从 (0,0) ~ (i,j) 区域的和
int dp[110][110] = {0};
for(int i = 1 ; i <= m;i++){
for(int j = 1; j <= n ;j++){
dp[i][j] = dp[i-1][j] + dp[i][j-1] - dp[i-1][j-1] + mat[i-1][j-1];
cout << dp[i][j] << " ";
}
cout <<endl;
}
//最终通过dp表快速的求出所需要的值
for(int i = 0; i < m;i++){
for(int j = 0; j < n ;j++){
int x1 = max(0,i - k) + 1;
int y1 = max(0,j - k) + 1;
int x2 = min(m-1,i + k) + 1;
int y2 = min(n-1,j + k) + 1;
// 求 (x1,y1) ~ (x2,y2) 区域的值给到ans即可
ans[i][j] = dp[x2][y2] - dp[x2][y1-1] - dp[x1-1][y2] + dp[x1-1][y1-1];
cout << ans[i][j] << " ";
}
cout << endl;
}
return ans;
}
};

