代码示例👇

//author:Mitchell_Donovan
//date:5.11
#include<iostream>
#include<queue>
#include<iomanip>//用于保留两位小数输出
using namespace std;

//边类
class Edge {
public:
	int from, to;
	double weight;
	Edge() {
		from = -1;
		to = -1;
		weight = 0;
	}
	Edge(int fromValue, int toValue, double weightValue) {
		from = fromValue;
		to = toValue;
		weight = weightValue;
	}
};

//图类
class Graph {
public:
	int numVertex;
	int numEdge;
	int* Mark;//标记图中顶点是否被访问过
	int* Indegree;//存放图中顶点的入度
	Graph(int num) {
		numVertex = num;
		numEdge = 0;
		Indegree = new int[numVertex];
		Mark = new int[numVertex];
		for (int i = 0; i < numVertex; i++) {
			Mark[i] = 0;//0表示未访问过
			Indegree[i] = 0;//入度设为0
		}
	}
	~Graph() {
		delete[]Mark;
		delete[]Indegree;
	}
	//判断是否为边
	bool isEdge(Edge oneEdge) {
		if (oneEdge.weight > 0 && oneEdge.weight < INFINITY && oneEdge.to >= 0) {
			return true;
		}
		else {
			return false;
		}
	}
	//访问
	void Visit(Graph& G, int v) {
		cout << v + 1 << " ";
		//cout << G.data[v];
	}
};

//用相邻矩阵表示图
class Graphm :public Graph {//类继承
private:
	double** matrix;//指向相邻矩阵的指针
public:
	Graphm(int num) :Graph(num) {
		matrix = (double**)new double* [numVertex];//申请二维数组空间
		for (int i = 0; i < numVertex; i++) {
			matrix[i] = new double[numVertex];
		}
		for (int i = 0; i < numVertex; i++) {//相邻矩阵初始化
			for (int j = 0; j < numVertex; j++) {
				matrix[i][j] = 0;
			}
		}
	}
	~Graphm() {
		for (int i = 0; i < numVertex; i++) {
			delete[]matrix[i];
		}
		delete[] matrix;
	}
	//返回顶点的第一条边
	Edge firstEdge(int oneVertex) {
		Edge myEdge;
		myEdge.from = oneVertex;
		for (int i = 0; i < numVertex; i++) {
			if (matrix[oneVertex][i] != 0) {
				myEdge.to = i;
				myEdge.weight = matrix[oneVertex][i];
				break;
			}
		}
		return myEdge;
	}
	//返回与已知边相同顶点的下一条边
	Edge nextEdge(Edge preEdge) {
		Edge myEdge;
		myEdge.from = preEdge.from;
		if (preEdge.to >= numVertex) {//不存在下一条边
			return myEdge;
		}
		for (int i = preEdge.to + 1; i < numVertex; i++) {
			if (matrix[preEdge.from][i] != 0) {
				myEdge.to = i;
				myEdge.weight = matrix[preEdge.from][i];
				break;
			}
		}
		return myEdge;
	}
	//为图设置一条边
	void setEdge(int from, int to, double weight) {
		if (matrix[from][to] <= 0) {//如果原边不存在
			numEdge++;
			Indegree[to]++;
		}
		matrix[from][to] = weight;
	}
	//删除图的一条边
	void delEdge(int from, int to) {
		if (matrix[from][to] > 0) {//如果原边存在
			numEdge--;
			Indegree[to]--;
		}
		matrix[from][to] = 0;
	}
};

//结构体Dist用于保存最短路径信息
struct Dist {
	int index;//顶点的索引项
	double length;//当前最短路径长度
	int pre;//路径最后经过的顶点
};

//最小生成树
void Prime(Graphm& G, int s) {//s是开始顶点，数组MST用于保存最小生成树的边
	int MSTtag = 0;//最小生成树的边计数
	Edge* MST = new Edge[G.numVertex - 1];
	Dist* D = new Dist[G.numVertex];
	for (int i = 0; i < G.numVertex; i++) {//初始化
		G.Mark[i] = 0;
		D[i].index = i;
		D[i].length = INFINITY;
		D[i].pre = s;
	}
	D[s].length = 0;
	G.Mark[s] = 1;
	int v = s;
	for (int i = 0; i < G.numVertex - 1; i++) {
		if (D[v].length == INFINITY) {//有不可达顶点，非连通图
			cout << "此图不连通！";
			return;
		}
		//因为v的加入，需要刷新与v相邻接的顶点的D值
		for (Edge e = G.firstEdge(v); G.isEdge(e); e = G.nextEdge(e)) {
			if (G.Mark[e.to] == 0 && (D[e.to].length > e.weight)) {
				D[e.to].length = e.weight;
				D[e.to].pre = v;
			}
		}
		//在D数组中找最小值记为v
		for (int j = 0; j < G.numVertex; j++) {
			if (G.Mark[j] == 0) {
				v = j;//让v为随意一个未访问的顶点
				break;
			}
		}
		for (int j = 0; j < G.numVertex; j++) {
			if (G.Mark[j] == 0 && (D[j].length < D[v].length)) {
				v = j;
			}
		}
		G.Mark[v] = 1;
		Edge myEdge(D[v].pre, D[v].index, D[v].length);
		MST[i] = myEdge;
		MSTtag++;
		cout << MST[i].from << "->" << MST[i].to << endl;
	}
	cout << "成功！";
}



int main() {
	int n, m;
	cout << "顶点个数：";
	cin >> n;
	Graphm test(n);
	cout << "图中边的个数：";
	cin >> m;
	int from, to;
	double weight;
	for (int i = 0; i < m; i++) {
		cout << "第" << i + 1 << "条边的起点、终点、权重：";
		cin >> from;
		cin >> to;
		cin >> weight;
		test.setEdge(from, to, weight);
		test.setEdge(to, from, weight);
	}
	cout << "开始构造最小生成树：" << endl;
	Prime(test, 0);
}

输入示例👇

顶点个数：7
图中边的个数：9
第1条边的起点、终点、权重：0 4 1
第2条边的起点、终点、权重：0 1 20
第3条边的起点、终点、权重：1 3 4
第4条边的起点、终点、权重：1 2 6
第5条边的起点、终点、权重：4 5 15
第6条边的起点、终点、权重：3 5 12
第7条边的起点、终点、权重：2 6 2
第8条边的起点、终点、权重：3 6 8
第9条边的起点、终点、权重：5 6 10

输出示例👇

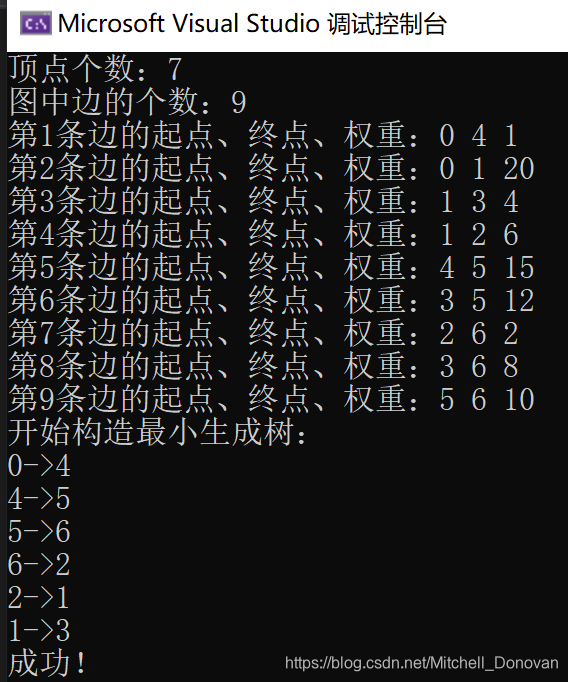
补充说明

Prime算法与Dijkstra算法相似。

不同的是Prime算法通过直接比较D数组元素来确定权重最小的边，适用于稠密图；

而Dijkstra算法采用的是优先队列，适用于稀疏图。