一. RoPE
1.为什么需要位置编码
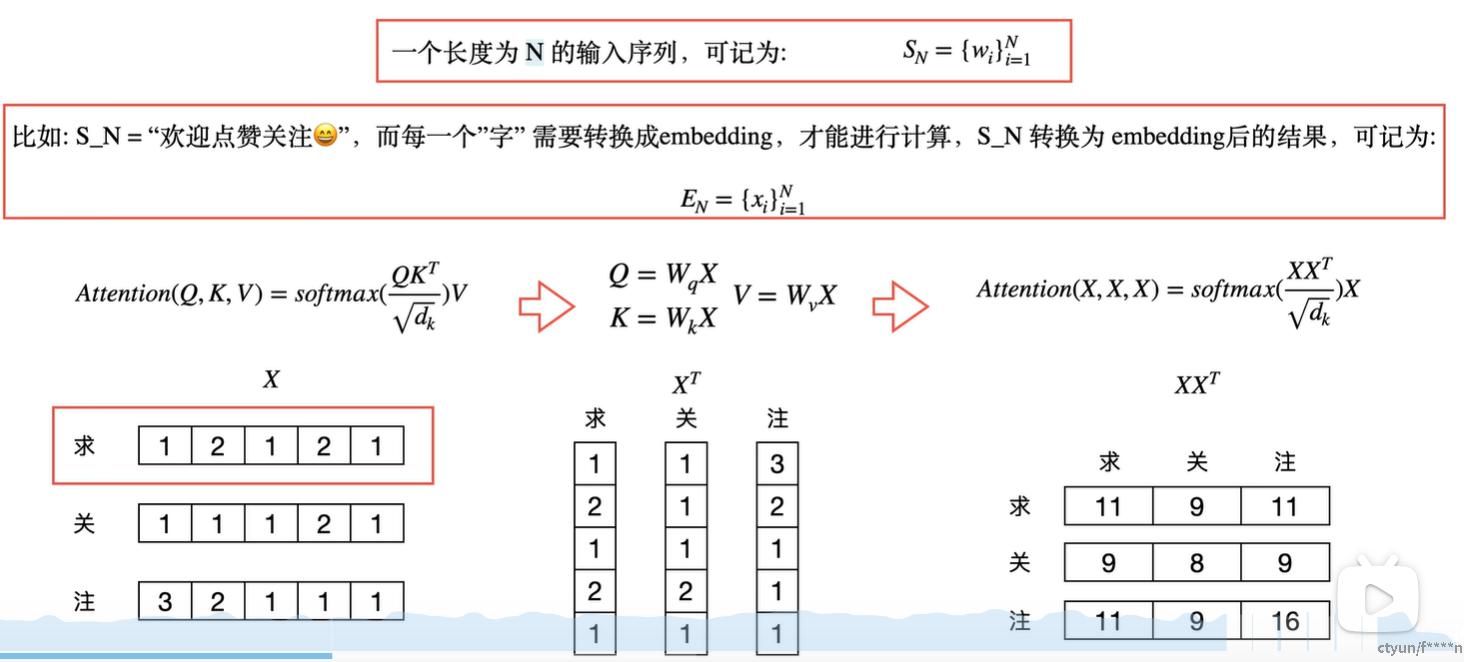
接下来计算注意力后的特征向量
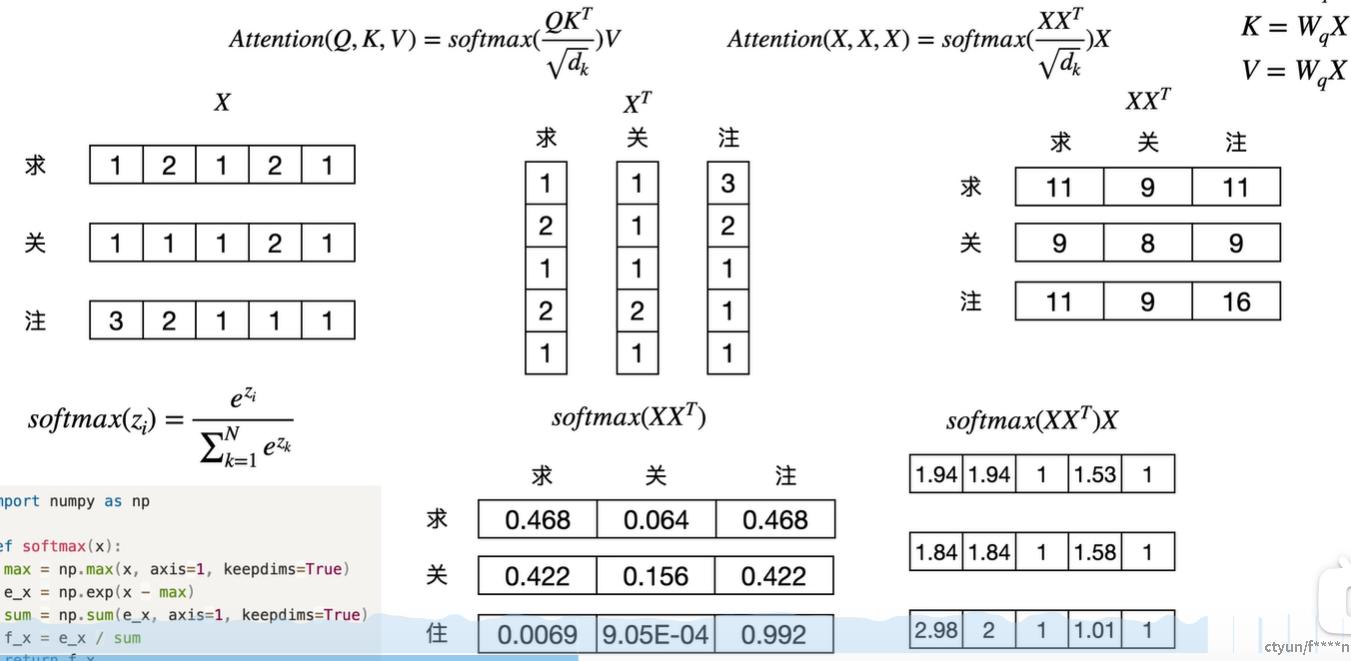
接下来思考一个问题:改变"求关注"的顺序再求自注意力
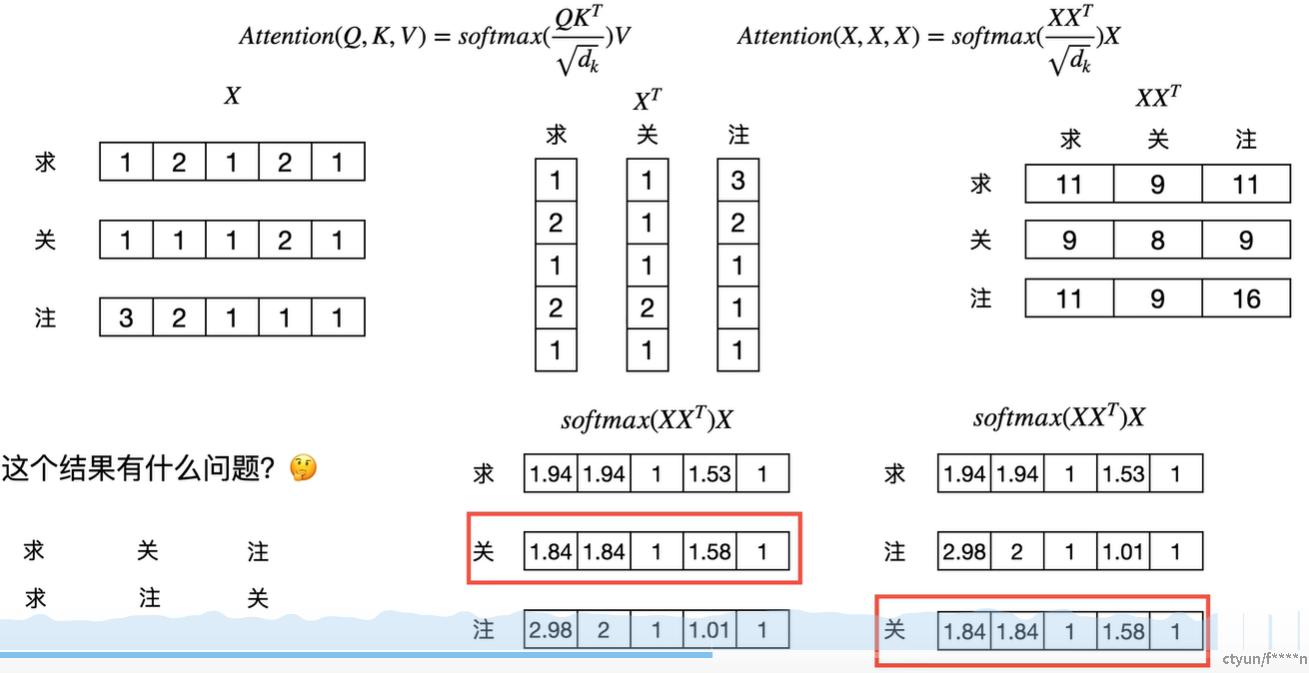
思考:"求关注"和"求注关"存在语义上的差别,其token的特征编码应该要体现差异
2.Embedding 如何体现文本的位置关系

最简单的方法: 构造f(x,i), i表示token的位置,引入位置编码
|
特性 |
绝对位置编码 |
旋转位置编码(RoPE) |
|
位置信息类型 |
绝对位置 |
绝对+相对位置 |
|
长序列支持 |
有限(正弦外推弱,可学习固定长度) |
极强(连续旋转支持任意长度) |
|
计算效率 |
高(简单加法) |
中(需旋转操作,但支持KV Cache优化) |
|
适用场景 |
短序列、简单任务 |
长文本生成、大模型推理 |
3.RoPE的数学理论
参考此篇文章
https://zhuanlan.zhihu.com/p/30190764463
苏神:https://spaces.ac.cn/archives/8265
4.RoPE的性质
4.1 远距离衰减
远距离衰减指的是随着q和k的相对距离的增大,加入位置编码之后的内积应该随着距离增大而减小,这样相当于离得远的token分配到的attention会比较小,而离得近的token会得到更多的注意力。这样的特性确实直觉上比较符合人类的注意力机制。
把各个参数(base、window size、head size)下的内积值画出来看看是怎么衰减的。实现参考下面的代码。这里偷懒没有实现得很高效,勉强能用就行。
|
参数 |
典型值 |
影响范围 |
示例模型 |
|
Base (θ) |
10000或动态调整 |
位置编码的频率分布 |
LLaMA(固定10000) |
|
Window Size (w) |
512或2048 |
注意力计算的实际范围 |
Longformer(滑动窗口) |
|
Head Size (dh) |
64、128或256 |
旋转操作的维度和多头注意力设计 |
|
Base:(通常记为 θ或 base)是控制旋转角度频率的超参数,决定了位置编码的波长分布。其计算公式通常为 θi=10000−2i/d,其中 d是向量的维度,i是维度索引。
作用:
控制旋转角度的变化速率:较大的 base值会使高频维度(靠近向量末尾的维度)旋转更慢,低频维度(靠近向量开头的维度)旋转更快,从而捕捉不同尺度的位置关系。
影响外推能力:合适的 base值能平衡短距离和长距离依赖的建模,例如在插值方法(如NTK-aware)中调整 base可以优化长序列处理能力
|
维度 i |
θi |
|
0 |
10000−0=1 |
|
1 |
10000−0.25≈0.56 |
|
2 |
10000−0.5≈0.01 |
|
3 |
10000−0.75≈0.0002 |
(1)q = k = 1
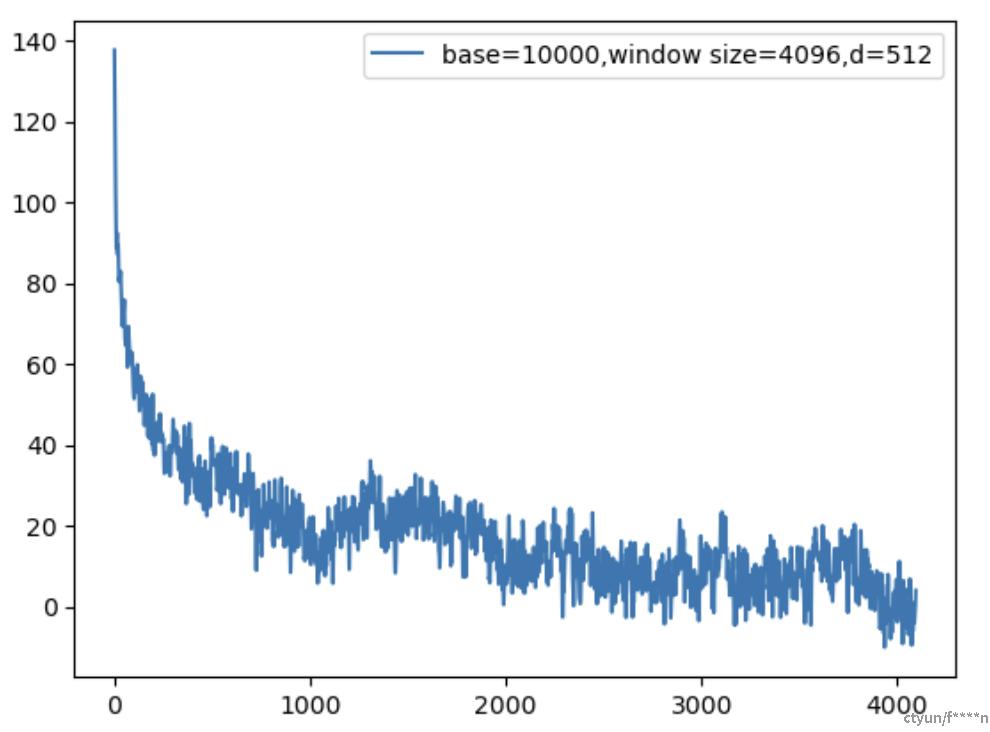
假设q和k都是1向量,如果q在位置0,画出k在0~4096位置下和q在位置编码后的内积如下。
这里使用了base=10000,d=512,可以看到整体趋势是震荡下降的。
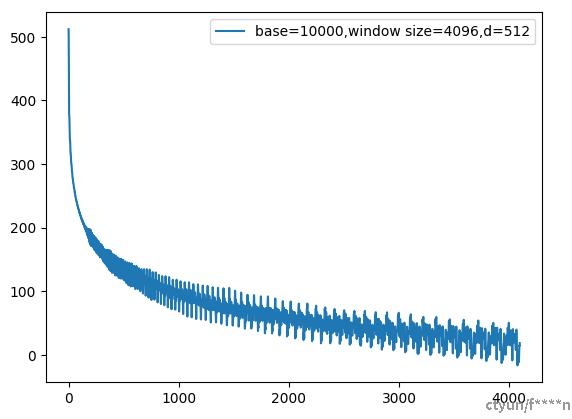
不过如果把窗口从4096增大到65536,图像会变成这样。
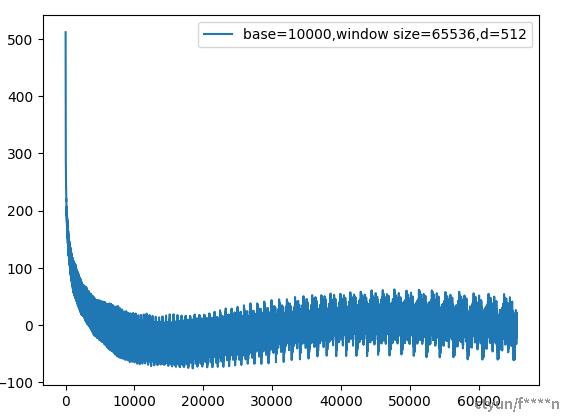
可以看到图像不再是单纯的衰减,在距离超过大约15000的时候,出现了上升。
实际上这个包含多个周期函数的内积也具有一定的周期性,并不是在整个域上保持衰减的特性。只要相对距离够大,超过这个周期的1/4,内积就会再次上升。
而这个内积的周期受base调控,base越大,周期越长,因此现在的长窗口模型起步就是base=5M或者10M。
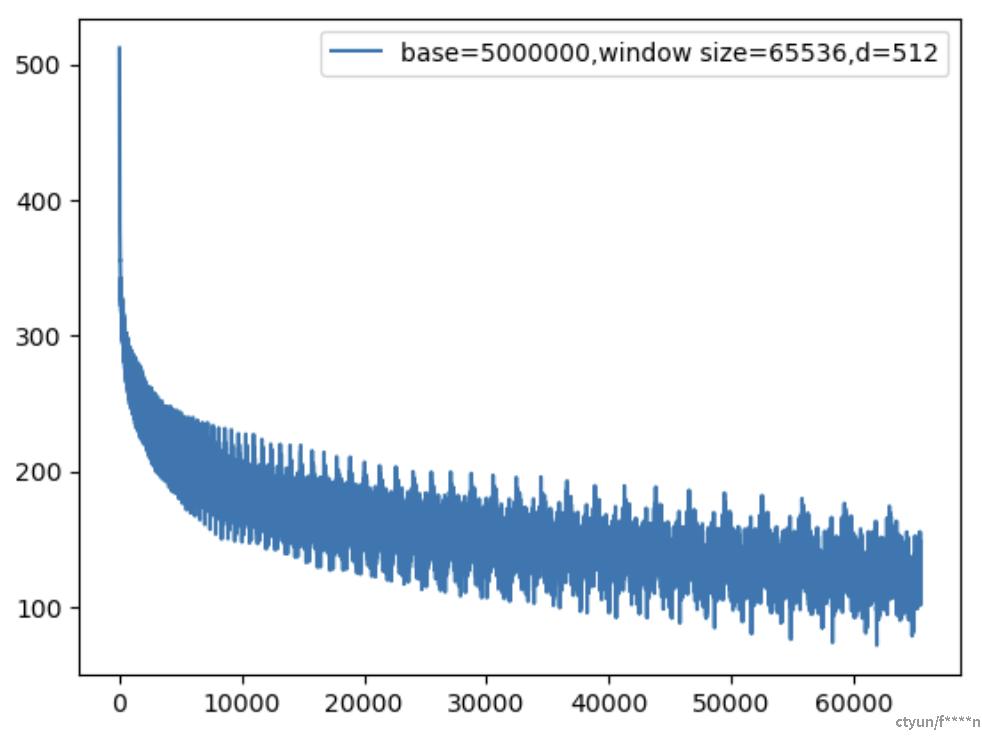
(2)q、k随机
前面是把q和k固定为1向量,现在试着把q和k初始化为随机向量,图像如下
相比1向量出现了更多的震荡,但是大体上还是能保持一定的远距离衰减特性。
- RoPE的远距离衰减是震荡的,并且整个内积本身也具有一定的周期性,只有把base设得足够大,才能让内积结果在模型窗口大小内保持远距离衰减的特性。
- 在q和k的相对距离小的时候,内积差距较大,也就是衰减较快;到了远距离之后,衰减变慢,也就是从内积角度来看,分辨率会变小。
5.RoPE与上下文拓展
6.1.推理外推
RoPE通过旋转矩阵将位置信息融入查询(Q)和键(K)向量中,其核心思想是:
(1)旋转操作:对向量的每一对维度施加旋转,旋转角度与位置线性相关(例如,位置 m的向量旋转 mθ角度)。这种设计使得两个向量的点积仅依赖于它们的相对距离 ∣m−n∣,而与绝对位置无关。因此,模型在训练时学习的是相对位置关系,而非固定长度的绝对位置编码
(2)连续性保证:旋转角度的连续变化(如 θi=10000−2i/d)确保了位置外推时角度的平滑过渡,避免了离散跳跃导致的信息断裂。即使遇到超出训练长度的位置,旋转后的向量仍能保持合理的几何关系
关键点:RoPE的旋转机制天然支持相对位置建模,使得模型在推理时能泛化到任意长度的序列,只要相对距离在训练范围内出现过
6.2.训练外推
比如YaRN外推训练:https://www.cnblogs.com/laozhanghahaha/p/18345815
7.RoPE的数学特性与KV Cache的兼容性
RoPE通过旋转矩阵将位置信息融入查询(Q)和键(K)向量中,其核心思想是对向量的每一对维度进行旋转变换。旋转角度与token的位置相关,但旋转矩阵本身是正交的,这意味着:
(1)位置信息解耦:RoPE将位置编码与向量内容分离,使得位置变换后的Q和K向量仍能通过点积保留相对位置关系。这种特性允许KV Cache存储未旋转的原始K向量,仅在计算注意力时动态应用旋转,避免了重复存储不同位置的K向量
(2)缓存原始K向量:由于RoPE的旋转操作是线性的,推理时只需缓存未旋转的K向量(或低秩压缩后的潜在向量),在需要时根据当前位置动态生成旋转后的K向量。这显著减少了KV Cache的存储需求,因为无需为每个位置单独缓存旋转后的K向量
(3)传统绝对位置编码(如正弦编码或可学习嵌入)需要将位置信息直接加到K向量中,导致KV Cache必须存储已编码的K向量,无法动态调整位置。而RoPE的旋转操作是位置相关的函数,允许K向量在缓存后仍能灵活适应不同位置,从而支持长序列推理
8.代码解读
```plaintext
import torch
def precompute_freqs_cis(dim, end, theta=10000):
# e^i*m*(10000)^-2i/d ->(10000)^(-2i/d) i->(0,2/d -1)
# 1/(10000**[0.0]/2) shape [1]
freqs = 1.0/(theta**(torch.arange(0, dim, 2)[:(dim//2)].float()/dim))
# [3]
m = torch.arange(end)
# [3],[1] ->[3,1]
freqs = torch.outer(m, freqs)
freqs_cis = torch.polar(torch.ones_like(freqs), freqs)
return freqs_cis
def reshape_for_broadcast(freqs_cis, x):
ndim = x.ndim
assert 0 <= 1 < ndim
assert freqs_cis.shape == (x.shape[1], x.shape[-1])
# [3,1] ->[1,3,1,1]
shape = [d if i==1 or i==ndim-1 else 1 for i, d in enumerate(x.shape)]
return freqs_cis.view(*shape)
def apply_rotary_emb(xq, xk, freqs_cis):
# 复数 实部+虚部 xq shape [1,3,2] [1,3,1,2] *xq.shape[:-1] [1,3,1,2] -> view_as_complex ->[1,3,1,1]
xq_ = torch.view_as_complex(xq.float().reshape(*xq.shape[:-1], -1, 2))
xk_ = torch.view_as_complex(xk.float().reshape(*xk.shape[:-1], -1, 2))
# freqs_cis [3,1] ->[1,3,1,1]
freqs_cis = reshape_for_broadcast(freqs_cis, xq_)
# q*e^I*m*theta
#[1,3,2] xq_*ffreqs_cis->[1,3,1,1]->view_as_real->[1,3,1,2]->[1,3,2]
xq_out = torch.view_as_real(xq_*freqs_cis).flatten(3)
# xq [1,3,1,2]->[1,3,1,1,2]->VIEW_CIMPLEX-》[1,3,1,1,1]->view_as_real->[1,3,1,1,2]->[1,3,1,2]
xk_out = torch.view_as_real(xk_*freqs_cis).flatten(3)
return xq_out.type_as(xq), xk_out.type_as(xq)
dim = 2
end = 3
fres_cis = precompute_freqs_cis(dim, end)
xq = torch.randn(1, end, dim)
xk = torch.randn(1, end, dim)
res = apply_rotary_emb(xq, xk, fres_cis)
print(res[0].shape)
```