传统的 MoE 架构用 MoE 层替代 Transformer 中的前馈网络 (FFN)。每个 MoE 层由多个专家组成，每个专家在结构上与标准 FFN 相同，每个 token 分配给一个或两个专家。
这种架构体现了两个潜在问题：
(1) 知识混合：现有的 MoE 通常雇用有限数量的专家（例如 8 位或 16 位），因此分配给特定专家的 token 可能会涵盖不同的知识。因此，指定的专家可能会在其参数中汇集截然不同类型的知识，这些知识很难同时利用。 (2) 知识冗余：分配给不同专家的 token 可能需要共同的知识。因此，多个专家可能会聚集在一起获取各自参数中的共享知识，从而导致专家参数冗余。

2.1 transformers的MOE架构

2.1.1 标准的transformers

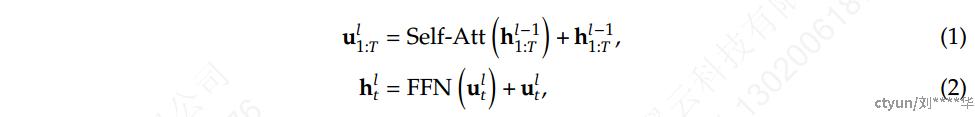
𝑇 表示序列长度，Self-Att(·) 表示自注意力模块，FFN(·) 表示前馈网络 (FFN)，**u_{1:T}^l∈ R^{T×d}**是第 𝑙 个注意力模块之后所有 token 的隐藏状态，**h_{t}^l∈ R^{d}**是第 𝑙 个 transformer block之后第 𝑡 个 token 的输出隐藏状态。

2.1.2 MOE的transformers

构建 MoE 语言模型的典型做法通常是用 MoE 层以指定的间隔替换 Transformer 中的 FFN。MoE 层由多位专家组成，其中每个专家在结构上与标准 FFN 相同。然后，每个 token 将被分配给一位或两位专家。如果用 MoE 层替换第 𝑙 个 FFN，则其输出隐藏状态h_{t}^l的计算表示为：

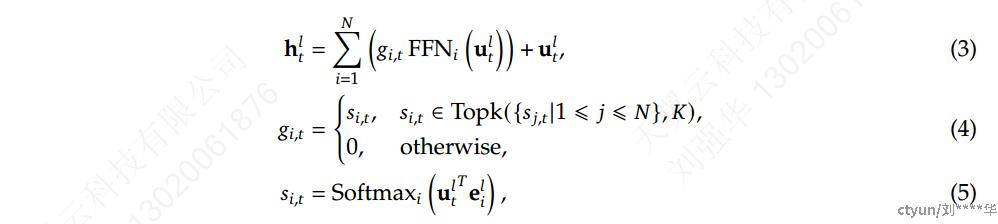
𝑁 表示专家总数，FFN𝑖(·) 是第 𝑖 位专家的 FFN，**g_{i,t}**表示第 𝑖 位专家的gate value，**s_{i,t}**表示 token 与专家的亲和力，Topk(·, 𝐾) 表示在第 𝑡 位 token 和所有 𝑁 位专家中计算出的 𝐾 个最高亲和力分数的集合，e_{i}^l是第 𝑙 层中第 𝑖 位专家的中心。**g_{i,t}**是稀疏的，表示𝑁 个gate value中只有的 𝐾 个非零。这种稀疏性确保了 MoE 层内的计算效率，即每个 token 将仅分配给 𝐾 专家并在其中计算。

2.2 DeepSeek-MoE 架构

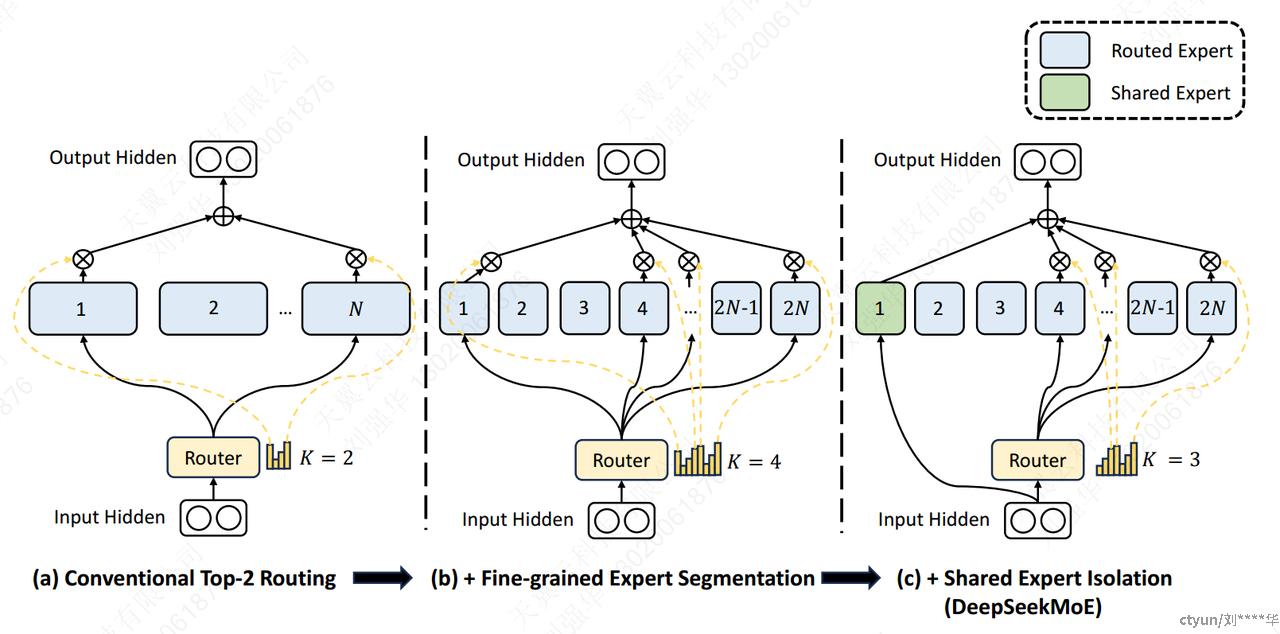
2.2.1 细粒度专家细分

在保持一致的专家参数数量和计算成本的同时，对专家进行了更细粒度的细分。更精细的专家细分使激活专家的组合更加灵活和适应性更强。在典型 MoE 架构之上，将每个专家 FFN 细分为 𝑚 个较小的专家，方法是将 FFN 中间隐藏维度减小到其原始大小的 1 /𝑚 倍。由于每个专家都变得更小，因此，作为响应，将激活专家的数量增加到 𝑚 倍以保持相同的计算成本，如上图 (b) 所示。通过细粒度专家细分，MoE 层的输出可以表示为：

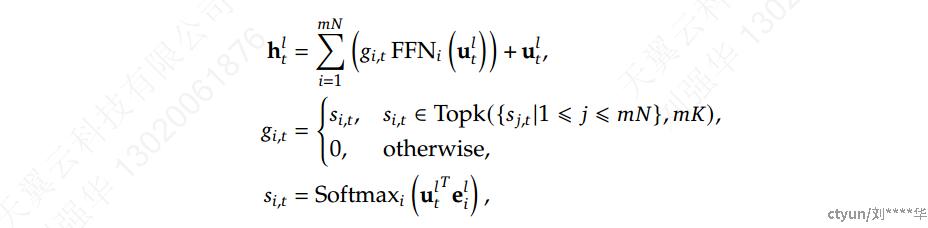
其中专家参数总数等于标准FFN中参数数量的𝑁倍，𝑚𝑁表示细粒度专家的总数。采用细粒度专家分割策略，非零gate value的数量也将增加到𝑚𝐾。
从组合角度来看，细粒度专家细分策略大大增强了激活专家的组合灵活性。
𝑁 = 16 ：

• 典型的Top-2 Routing策略可以产生 C_{16}^2= 120 种可能的组合。
• 如果将每个专家分成 4 个较小的专家，fine-grained experting策略可以产生C_{64}^8= 4,426,165,368 种潜在组合。

2.2.2 共享专家隔离

在传统的Routing策略中，分配给不同专家的tokens可能需要一些共同的知识或信息。因此，多个专家可能会集中获取各自参数中的共同知识，从而导致专家参数的冗余。
方法：隔离K_{s}专家以作为共享专家。无论router模块如何，每个token都将确定性地分配给这些共享专家。为了保持恒定的计算成本，其他路由专家中激活的专家数量将减少K_{s}，如上图 (c) 所示。集成共享专家隔离策略后，完整的 DeepSeekMoE 架构中的 MoE 层公式如下：

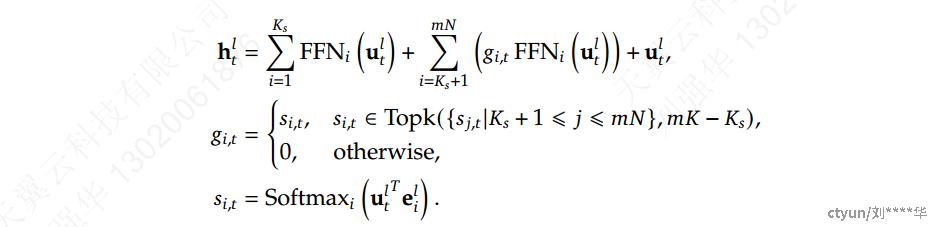
2.2.3 负载平衡考虑

专家级平衡损失

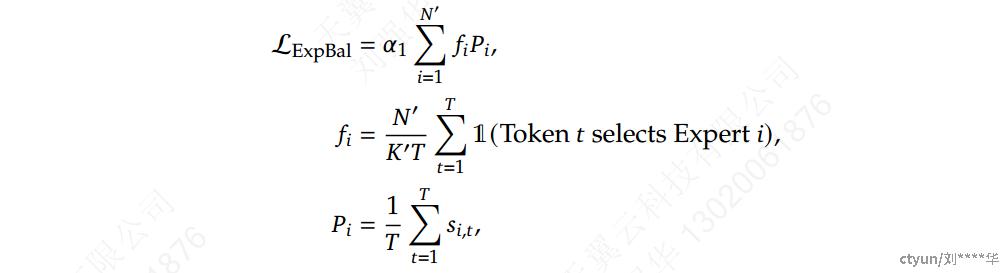
尽量使每个专家应该处理相同数量的数据，以实现资源的均匀利用，其中**\alpha_1**是一个超参数，称为专家级平衡因子，𝑁 ′ = (𝑚𝑁 − 𝐾𝑠)，𝐾 ′= (𝑚𝐾 − 𝐾𝑠)

设备级平衡损失

确保设备之间的计算平衡，如果将所有路由专家划分为 𝐷 组**\{{\largeε_1},{\largeε_2},...,{\largeε_D}\}**，并将每个组部署在单个设备上，则设备级平衡损失的计算方式如下：

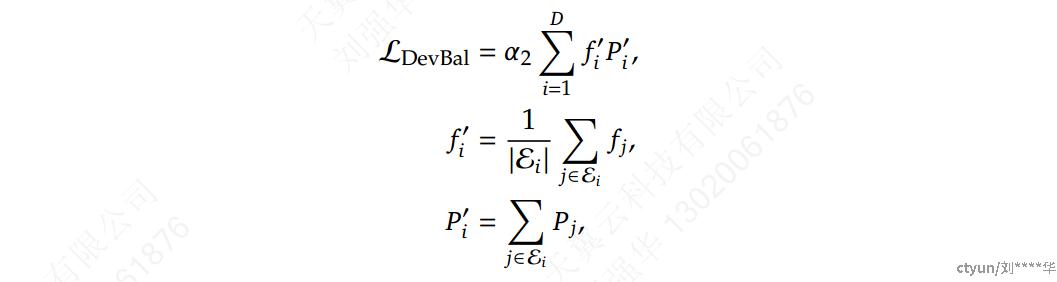
\alpha_2是一个超参数，称为设备级平衡因子